基於傅立葉變換和PyQt4開發一個簡單的頻率計數器
小學期的《訊號與系統》課,要求寫一個頻率計數器,下面是我個人理解的頻率計數
傅立葉變換的程式碼:
# coding=utf-8 import numpy as np from scipy.io import wavfile import matplotlib.mlab as mlab import matplotlib.pyplot as plt class FrequencyCounter(): def loaddata(self, filename): try: samplerate, channels = wavfile.read(filename) self.data = np.mean(channels, axis=1) except: raise ValueError, 'Data Error' def fft(self, windowsize=4096, samplerate=44100, overlapratio=0.5): try: self.res = plt.specgram(self.data, NFFT=windowsize, Fs=samplerate, window=mlab.window_hanning, noverlap=int(windowsize * overlapratio))[0] #傅立葉變換,引數是滑動視窗大小和樣例頻率 from numpy.core.umath_tests import inner1d #計算內積 for i in xrange(len(self.res)): self.res[i] = inner1d(self.res[i], self.res[i]) #plt.plot([x for x in xrange(len(self.res))],self.res) except: raise ValueError, 'No Data for FFT' def mainfrequency(self): def compare(a, b): return int(a[0][0] < b[0][0]) sortlist = [i for i in range(len(self.res))] for i in range(len(sortlist)): sortlist[i] = (self.res[i], i) sortlist.sort(lambda x, y: cmp(sum(x[0]), sum(y[0]))) #按照內積大小結果排序 #for i in sortlist[:200]: #print i[1] return sortlist[:5] def draw(self): ''' 畫圖,為GUI提供圖片 ''' #plt.figure(figsize=(8,4)) plt.plot([i for i in xrange(len(self.data))], self.data) plt.title(u'音訊訊號波形',fontproperties='SimHei') #plt.show() plt.savefig('wave.jpg',dpi=70) plt.cla() plt.plot([i for i in xrange(len(self.res))], self.res) plt.title(u'音訊訊號頻譜分析',fontproperties='SimHei') #plt.show() plt.savefig('frequency.jpg',dpi=70) if __name__ == '__main__': p = FrequencyCounter() p.loaddata('python-audio\\output2.wav') p.fft() p.draw()
PyQt4開發GUI的程式碼:
# -*- coding: utf-8 -*- from PyQt4.QtGui import * from PyQt4.QtCore import * import sys import frequency_counter2 p = frequency_counter2.FrequencyCounter() class UI(QDialog): def __init__(self, parent=None): super(UI, self).__init__(parent) self.txt = QLineEdit() self.bt_ad = QPushButton(u"選擇路徑") self.bt_a = QPushButton(u"分析") self.txtout = QTextEdit() self.pic1 = QLabel() self.pic2 = QLabel() lay = QGridLayout() #網格佈局 lay.addWidget(self.txt, 1, 1) lay.addWidget(self.bt_ad, 1, 2) lay.addWidget(self.bt_a, 2, 1, 1, 2) lay.addWidget(self.pic1, 4, 1, 3, 3) lay.addWidget(self.pic2, 7, 1, 3, 3) self.setLayout(lay) self.connect(self.bt_a, SIGNAL("clicked()"), self.analy) self.connect(self.bt_ad, SIGNAL("clicked()"), self.addr) def analy(self): #self.txtout.setText("test") pix1 = QPixmap("wave.jpg") pix2 = QPixmap("frequency.jpg") self.pic1.setPixmap(pix1) self.pic2.setPixmap(pix2) def addr(self): fname = QFileDialog.getOpenFileName(self, 'Open file') print fname p.loaddata(fname) p.fft() p.draw() self.txt.setText(fname) if __name__ == "__main__": app = QApplication(sys.argv) ui = UI() ui.setWindowTitle(u"音訊訊號頻率分析") ui.show() app.exec_()
執行時介面:
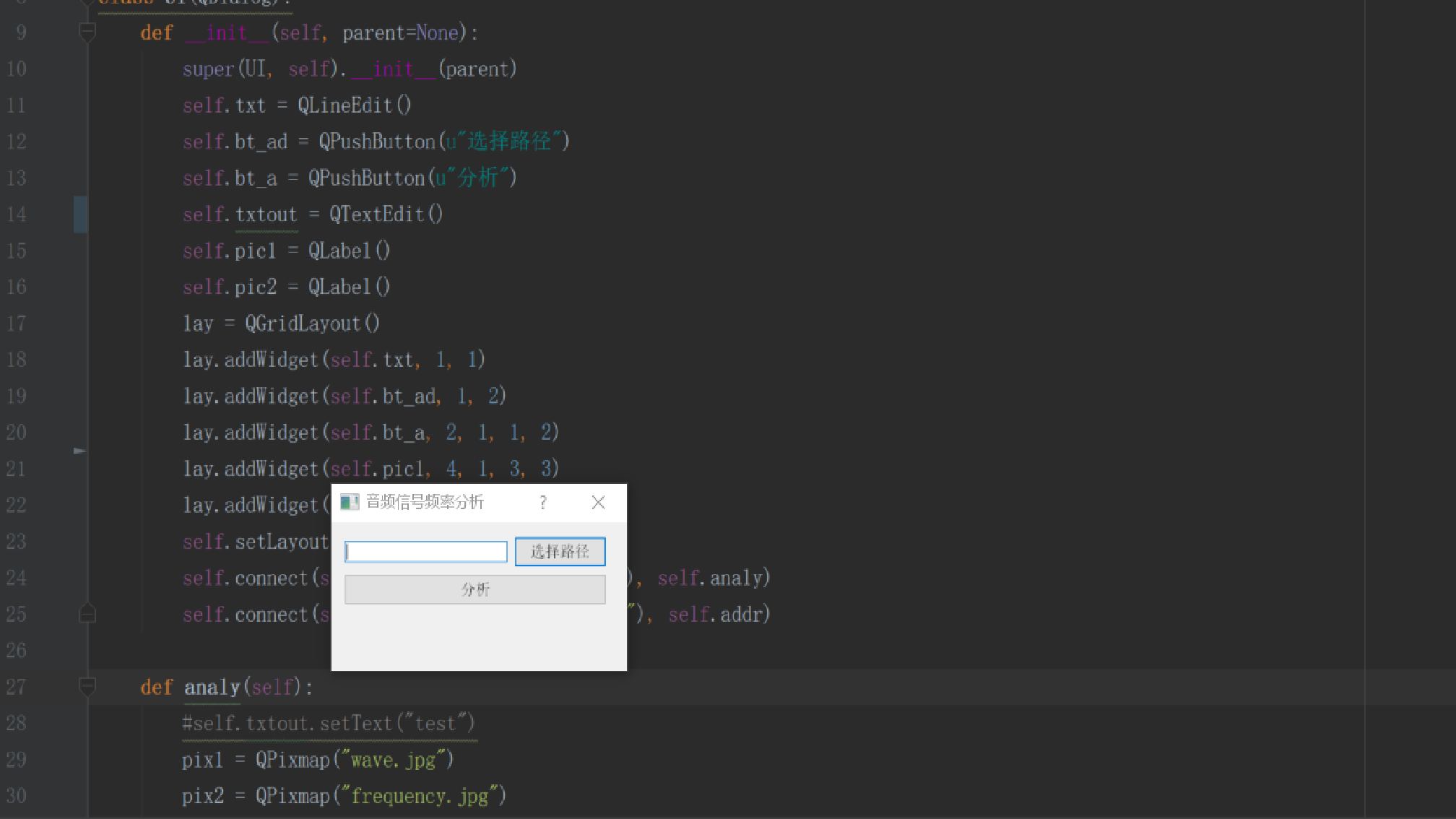
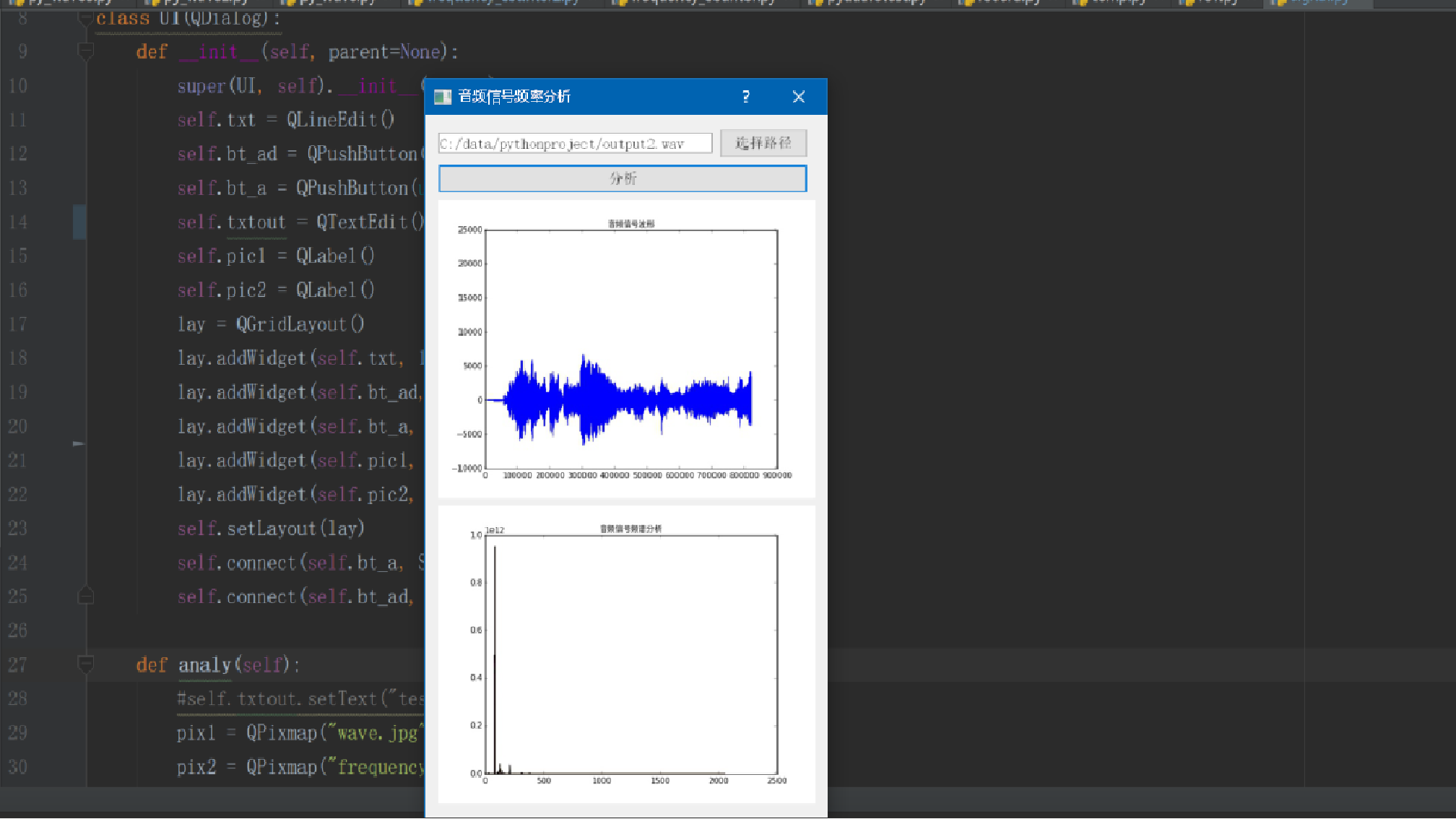
相關推薦
基於傅立葉變換和PyQt4開發一個簡單的頻率計數器
小學期的《訊號與系統》課,要求寫一個頻率計數器,下面是我個人理解的頻率計數 傅立葉變換的程式碼: # coding=utf-8 import numpy as np from scipy.io import wavfile import matplotlib.mlab as mlab import matp
【GCN】圖卷積網路初探——基於圖(Graph)的傅立葉變換和卷積
本文為從CNN到GCN的聯絡與區別——GCN從入門到精(fang)通(qi)的閱讀筆記,文中絕大部分公式和圖片摘自原文。 文章目錄 一、CNN(卷積神經網路)中的離散卷積 二、GCN基本概念介紹 (一)圖Grap
傅立葉變換 和 Gabor小波
1.傅立葉變換 1) 簡介 數字影象處理的方法主要分成兩大部分:空域分析法和頻域分析法。空域分析法就是對影象矩陣進行處理;頻域分析法是通過影象變換將影象從空域變換到頻域,從另外一個角度來分析影象的特徵並進行處理。頻域分析法在影象增強、影象復原、影象編碼壓縮及特徵編碼壓縮方
11.頻域裡的卷積——介紹,傅立葉變換和卷積,快速傅立葉變換(FFT)_1
目錄 介紹 FFT 介紹 我們將繼續討論頻率分析以及如何用頻率分量的概念來研究影象。如果你還記得上次我們講過的基於頻率的影象分解的概念。我們通過給你們看這張照片來回憶它(如圖)。這是著名的Dali圖片,當你在那裡允許高頻影象時,你會看到一個女人在欣賞地中海之類的東
分別用OpenCV-Python和Numpy實現傅立葉變換和逆傅立葉變換
Numpy實現 fft = np.fft.fft2(img) 將空間域轉化為頻率域 OpenCV實現 dft = cv2.dft(np.float32(img),flag=cv2.DFT_COMPLEX_OUTPUT) 這個函式與np.fft.fft2(img)實現相同的功能,但要注意先
傅立葉變換和拉普拉斯變換
尤拉公式 證明過程如下 首先是泰勒展開 參考cosX和sinX的泰勒展開可以證明這個問題。 還有下面這個號稱宇宙最美公式 “自然底數e,自然數1和0,虛數i還有圓周率pi,它是這麼簡潔,這麼美麗啊!” 傅立葉級數 傅立葉在提出傅立葉變換時,堅持認為任何一個週期訊號都可
影象處理複習2——影象傅立葉變換和頻域濾波
影象處理複習 CH4 基本影象變換 4.1 DFT (1)一維DFT 一維DFT: F(u)=1N∑N−1x=0f(x)e−j2πuxN,x=0,1,…,N−1 其逆變換: f(x)=∑N−1u=0F(u)ej2πuxN,u=0,1
OpenCV下利用傅立葉變換和逆變換實現影象卷積演算法,並附自己對於卷積核/模板核算子的理解!
學過訊號與系統的人都知道,卷積運算一般是轉化成頻率乘積再求逆來計算,因為這樣可以減少計算量,提高程式碼的效率。 影象卷積操作廣泛應用在影象濾波技術中。 影象卷積運算中一個重要概念是卷積核算子,它是模板核算子的一種,模板核算子實際上就是一個視窗矩陣,用這個視窗按畫素點滑動去
OpenCV—python 影象矯正(基於傅立葉變換—基於透視變換)
影象校正執行環境 Anaconda| pycharm/jupyter notebook 你需要安裝如下庫 pip install numpy pip install matplotlib pip install opencv-python 一、基於傅立葉變換
傅立葉變換和小波分析
無論是傅立葉變換還是小波變換,其實質都是一樣的,既:將訊號在時間域和頻率域之間相互轉換,從看似複雜的資料中找出一些直觀的資訊,再對它進行分析。由於訊號往往在頻域有比在時域更加簡單和直觀的特性,所以,大部分訊號分析的工作是在頻域中進行的。音樂——其實就是時/頻分析的一個極好
OpenCV基於傅立葉變換以及霍夫直線檢測的旋轉文字校正
最近剛好結束了霍夫三部曲以及離散傅立葉變換的總結,剛好了解到它們兩個的結合可以實現一個很有意思的功能 旋轉文字影象的校正,於是參考了幾篇部落格,記錄下來。 主要參考部落格: 標準霍夫直線檢測 以及影象的傅立葉變換 關於傅立葉變換的原理請看我的上一篇部落格,也是為這篇文章
傅立葉變換和逆變換公式的我理解意義
f(t)的傅立葉變換F(w)=∫ f(t) *e(-iwt)dt ,由於(1,sinwx,coswx,sin2wx,cos2wx,... sinnwx,cosnwx,....)是一組正交函式,傅立葉變換從公式來看就是內積,只有f(t)中含有對應w分 量才能有內積不為零,有
傅立葉變換和傅立葉級數的區別與聯絡(後續更新補充DTFT、DFS)
傅立葉級數僅適用於週期訊號,傅立葉變換可以視作傅立葉級數的延伸,可以用於分析非週期訊號的頻譜特性。事實上,引入衝擊函式後,週期訊號也可以進行傅立葉變換。 傅立葉級數:所有周期訊號都可以分解為不同頻率的
Python 實現影象快速傅立葉變換和離散餘弦變換
影象的正交變換在數字影象的處理與分析中起著很重要的作用,被廣泛應用於影象增強、去噪、壓縮編碼等眾多領域。本文手工實現了**二維離散傅立葉變換**和**二維離散餘弦變換**演算法,並在多個影象樣本上進行測試,以探究二者的變換效果。 ## 1. 傅立葉變換 ### 實驗原理 對一幅影象進行**離散傅立葉變換
離散傅立葉變換(DFT)和快速傅立葉變換(FFT)原理與實現
目錄 1、影象變換 2、離散傅立葉變換(Discrete Fourier Transform) 3、DFT性質 4、DFT與數字影象處理 5、FFT-快速傅立葉變換 6、DFT與FFT的演算法實現 1. 影象變換 — —數學領域中有很多種變換,如傅立葉變換、拉普拉斯變
傅立葉變換的意義和理解(通俗易懂)
這篇文章的核心思想就是:要讓讀者在不看任何數學公式的情況下理解傅立葉分析。 傅立葉分析不僅僅是一個數學工具,更是一種可以徹底顛覆一個人以前世界觀的思維模式。但不幸的是,傅立葉分析的公式看起來太複雜了,所以很多大一新生上來就懵圈並從此對它深惡痛絕。老實說,這麼有意思的東西居然成了大學裡的殺
真正理解傅立葉級數和傅立葉變換
真正理解傅立葉級數和傅立葉變換 記得上大學的時候的機械振動還有工程測試利用的傅立葉變化,當時感覺雲裡霧裡的,感覺好難,也就沒有去搞,渾水摸魚也就過來了,然後現在到了研究生階段,發現傅立葉變換呀,卷積呀非常的重要,也是學術研究最基礎的工具。在做人臉識別的時候剛好用上,所以靜下心
基於python的快速傅立葉變換FFT(二)
基於python的快速傅立葉變換FFT(二)本文在上一篇部落格的基礎上進一步探究正弦函式及其FFT變換。 知識點 FFT變換,其實就是快速離散傅立葉變換,傅立葉變換是數字訊號處理領域一種很重要的演算法。要知道傅立葉變換演算法的意義,首先要了解傅立葉原理的意義。傅立葉原理表明:任何連續測量的時序或訊號,都可
簡述計算機三大變換的聯絡和區別 (傅立葉變換 拉普拉斯變換 z變換)
Q:簡述計算機三大變換的聯絡和區別 (傅立葉變換 拉普拉斯變換 z變換) (1) 傅立葉變換定義: 表示能將滿足一定條件的某個函式表示成三角函式(正弦和/或餘弦函式)或者它們的積分的線性組合。傅立葉變換是一種分析訊號的方法,它可分析訊號的成分,也可用這
matlab進行傅立葉變換fft和shiftfft
使用matlab進行傅立葉變換 模擬訊號進行奈奎斯特取樣後成為離散的數字訊號,時域分析不太方便,通常要進行頻域變換更好的分析訊號,matlab中的fft和shiftfft兩個函式可以快速的幫助我們進行頻譜分析。兩個函式存在一些差別。 關於fft的預備知識: 由奈奎斯特取樣定理知,
