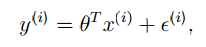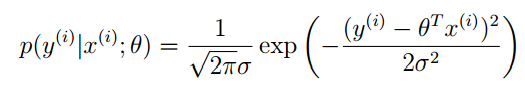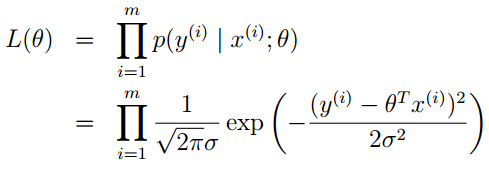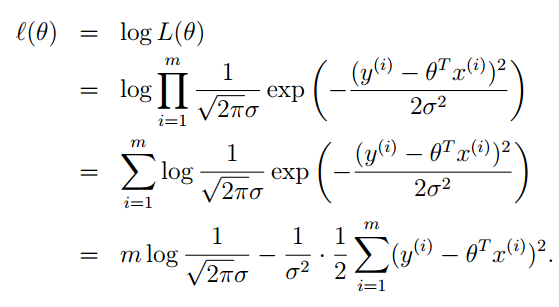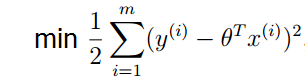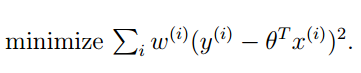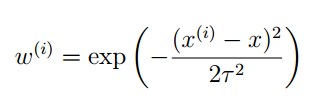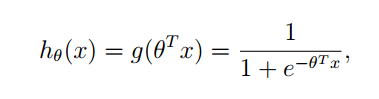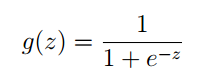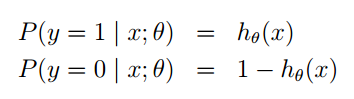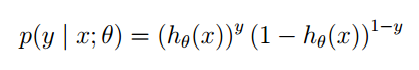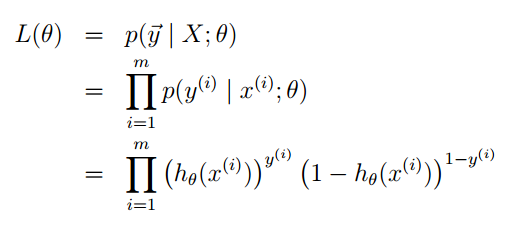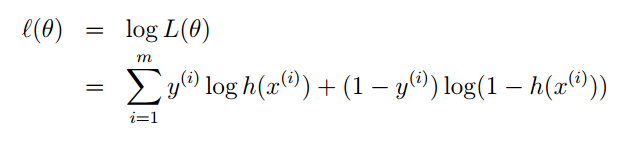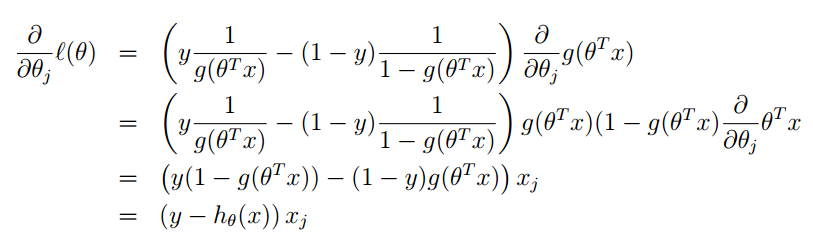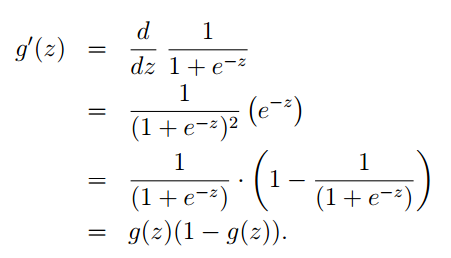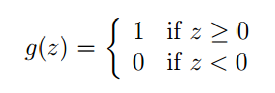斯坦福Andrew Ng---機器學習筆記(二):Logistic Regression(邏輯迴歸)
內容提要
這篇部落格的主要內容有:
- 介紹欠擬合和過擬合的概念
- 從概率的角度解釋上一篇部落格中評價函式J(θ)” role=”presentation” style=”position: relative;”>J(θ)J(θ)為什麼用最小二乘法
- 區域性加權線性迴歸(Locally Weighted Linear Regression (LWR))
- 邏輯迴歸(Logistic regression)
- 感知器學習演算法(The perceptron learning algorithm)
欠擬合與過擬合
我覺得欠擬合和過擬合都是從擬合的逼近訓練集程度上說的。本身擬合就是對訓練集特徵提取的過程,那麼就存在到底要精細到什麼樣的層次,這也就引出了欠擬合和過擬合的概念。這兩個概念是相對的不是絕對的。
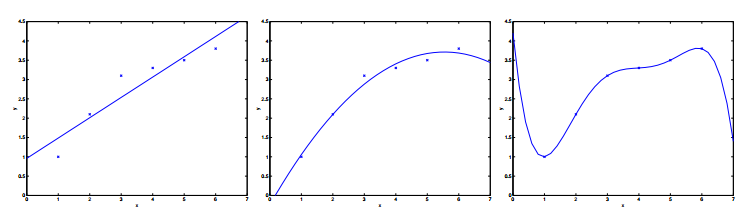
如下圖:
對待同樣的訓練集我們可以用線性函式去擬合,也可以用二次,當然也可以用高次。三種擬合方式一次對應上面三幅圖。Andrew Ng老師說就這個列子而言,第一種就是欠擬合,即擬合效果不好。第三種就是過擬合,同樣擬合效果也不好。第二種是比較好的一個擬合。總之,擬合的效果好不好還是得靠實驗結果。
為什麼線性擬合的評價函式要用最小二乘法
回顧上一篇部落格中講的例子,我們現在可以把線性迴歸的模型寫成下面的樣子:
上標i” role=”presentation” style=”position: relative;”>ii。為什麼假設是正態分佈,Andrew Ng老師解釋說主要有兩個原因:
- 一般的,訓練集中的因素的都是獨立的,而且對於某一種大量因素而言一般也都服從正態分佈,比如我們的身高。根據中心極限定理(中心極限定理:設從均值為μ” role=”presentation” style=”position: relative;”>μ
- Andrew Ng老師說這樣是為了計算的方便
根據y” role=”presentation” style=”position: relative;”>yy的概率密度如下:
注意:這裡的p(y(i)|x(i);θ)” role=”presentation” style=”position: relative;”>p(y(i)|x(i);θ)p(y(i)|x(i);θ)的概率。
我們將y(i)” role=”presentation” style=”position: relative;”>y(
為了便於計算,我們對似然函式去對數,自然數為底。我們一般寫成ln” role=”presentation” style=”position: relative;”>lnln,表示的是一個意思。
減號前半部分都是常數,最大似然估計就是要讓l(θ)” role=”presentation” style=”position: relative;”>l(θ)l(θ),去最大值。則就要求減號後面的部分取最小值。
這就證明了上篇部落格中提到的評價函式的正確性。
區域性加權線性迴歸(Locally Weighted Linear Regression (LWR))
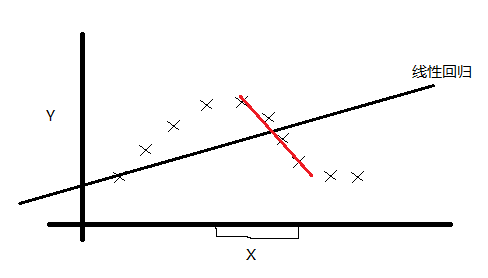
我們先來看下面訓練集:
如果用我們之前的線性迴歸,顯然是一個欠擬合。那麼我們怎麼改進呢?可能你想到了非線性迴歸,有人就想到了:採用區域性線性迴歸的方式對上面的訓練集進行擬合。經過實踐,這種想法也是非常有效的。我們再來看看怎麼用數學的方式體現區域性擬合。我們的想法就是線上性迴歸的評價函式中新增一個具有區域性性質的權重。如下:
其中的這個ω(i)” role=”presentation” style=”position: relative;”>ω(i)ω(i)個訓練樣本的權重係數。這個權重係數具有下面的性質:
- 如果|x(i)−x|” role=”presentation” style=”position: relative;”>|x(i)−x||x(i)−x|
- 如果|x(i)−x|” role=”presentation” style=”position: relative;”>|x(i)−x||x(i)−x|
這個權重係數就可以提現區域性特性了,式子中τ” role=”presentation” style=”position: relative;”>ττ是波長引數,控制了權值隨距離的下降速率,是一個實驗引數。可能你覺得這個權重係數的表達是和正態分佈的概率密度特別像,但是這裡沒有正態分佈的這層含義。可能你也覺得選擇其他的係數表示式可能更好,是的,這的確存在爭議,但是一般情況下選擇這個係數表示式,擬合效果比較好。當然你也可以具體情況具體分析。
上面這些如何選擇係數表示式,你可能不太在意。可能比較糾結ω(i)” role=”presentation” style=”position: relative;”>ω(i)ω(i),這時就可以預測房價了。
總結一下:LWR演算法是我們遇到的第一個non-parametric(非引數)學習演算法,而線性迴歸則是我們遇到的第一個parametric(引數)學習演算法。所謂引數學習演算法它有固定的明確的引數,引數 一旦確定,就不會改變了,我們不需要在保留訓練集中的訓練樣本。而非引數學習演算法,每進行一次預測,就需要重新學習一組,θ” role=”presentation” style=”position: relative;”>θθ向量是變化的,所以需要一直保留訓練樣本。也就是說,當訓練集的容量較大時,非引數學習演算法需要佔用更多的儲存空間,計算速度也較慢。有得必有失,效果好當然要犧牲一些其他的東西。
邏輯迴歸(Logistic regression)
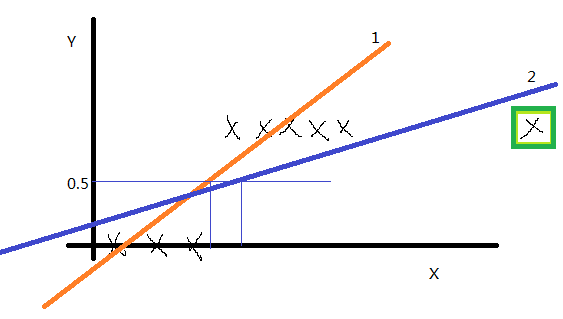
我們先看一個訓練集,如下圖:
如果y” role=”presentation” style=”position: relative;”>yy的取值只有0和1,訓練集畫出來這這個樣子(先沒有綠框中的點),我們用線性迴歸得到1號直線,如果認為模擬直線的取值小於0.5時則預測值就為0,如果模擬直線的取值大於0.5時預測值就為1,感覺還不錯。但是將綠框中的點加入後,線性迴歸得到的直線2,就顯得不是很完美了。經過大量的實驗證明,線性迴歸不適合這種訓練集。那麼怎麼解決這個問題呢?
我們提出來了一種新的迴歸模型:
其中g” role=”presentation” style=”position: relative;”>gg的函式原型為:
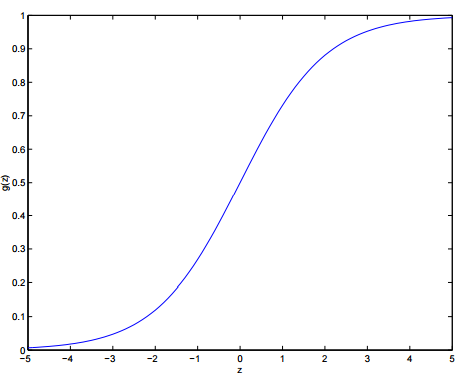
它的影象為:
可以看出:
- 當z>0” role=”presentation” style=”position: relative;”>z>0z>0
- 當z<0” role=”presentation” style=”position: relative;”>z<0z<0
g(z)” role=”presentation” style=”position: relative;”>g(z)g(z)這個函式稱之為:logistic function 或者 sigmoid function
利用g(z)” role=”presentation” style=”position: relative;”>g(z)g(z)函式,我們做出如下假設:
同樣的這裡P(y=1|x;θ)” role=”presentation” style=”position: relative;”>P(y=1|x;θ)P(y=1|x;θ)並不是表示條件概率,是一種類似最大似然估計的表示方式,表示出引數。也可以將他們寫在一塊,如下:
你可以把y” role=”presentation” style=”position: relative;”>yy的值帶入驗證,結果是正確的。
我們還是利用最大似然估計的思想去求引數,先構造似然函式。
然後去對數:
最大似然估計就是要讓l(θ)” role=”presentation” style=”position: relative;”>l(θ)l(θ)的梯度就可以了:
其中對於g(θTx)” role=”presentation” style=”position: relative;”>g(θTx)g(θTx)的求導可以參考下面:
總結一下:邏輯迴歸,和線性迴歸其本質思想上是一致的。都是利用概率的思想,把我們的估計值當成一個隨機變數,我們的訓練集就是一組抽樣。之後再利用最大似然估計,求其中的引數。當其中的引數求出來後,我們也就得到了迴歸方程,就可以進行預測或者其他工作了。
感知器學習演算法(The perceptron learning algorithm)
這個演算法是對邏輯迴歸的強行約束,使得函式值取0和1。定義形式如下:
同樣的我們假設hθ(x)=g(θTx)” role=”presentation” style=”position: relative;”>hθ(x)=g(θTx)hθ(x)=g(θTx)向量。整個推導過程和邏輯迴歸一樣,最終結果如下:
總結
現在我已經學習的梯度下降演算法屬於引數學習演算法,區域性加權線性迴歸屬於非引數學習演算法,感知器學習演算法屬於聚類演算法。他們都屬於監督學習這個大類。
end
相關推薦
斯坦福Andrew Ng---機器學習筆記(二):Logistic Regression(邏輯迴歸)
內容提要 這篇部落格的主要內容有: - 介紹欠擬合和過擬合的概念 - 從概率的角度解釋上一篇部落格中評價函式J(θ)” role=”presentation” style=”position: relative;”>J(θ)J(θ)為什麼用最
Andrew Ng 機器學習筆記(二)
監督學習的應用:梯度下降 梯度下降演算法思想: 先選取一個初始點,他可能是0向量,也可能是個隨機點。在這裡選擇圖中這個+點吧。 然後請想象一下:如果把這個三點陣圖當成一個小山公園,而你整站在這個+
非監督學習之混合高斯模型和EM演算法——Andrew Ng機器學習筆記(十)
0、內容提要 這篇博文主要介紹: - 混合高斯模型(mixture of Gaussians model) - EM演算法(Expectation-Maximization algorithm) 1、引入 假設給定一個訓練集{x(1),...,x(m)
學習理論之模型選擇——Andrew Ng機器學習筆記(八)
內容提要 這篇部落格主要的內容有: 1. 模型選擇 2. 貝葉斯統計和規則化(Bayesian statistics and regularization) 最為核心的就是模型的選擇,雖然沒有那麼多複雜的公式,但是,他提供了更加巨集觀的指導,而且很多時候
非監督學習之k-means聚類演算法——Andrew Ng機器學習筆記(九)
寫在前面的話 在聚類問題中,我們給定一個訓練集,演算法根據某種策略將訓練集分成若干類。在監督式學習中,訓練集中每一個數據都有一個標籤,但是在分類問題中沒有,所以類似的我們可以將聚類演算法稱之為非監督式學習演算法。這兩種演算法最大的區別還在於:監督式學習有正確答
機器學習筆記(二):python 模組pandas
1.讀csv檔案資料 import pandas as pd Info = pd.read_csv('titanic_train.csv'); #print(type(Info)) #Info的型別 <class 'pandas.core.frame
機器學習筆記(二):線性模型
線性模型是機器學習常用的眾多模型中最簡單的模型,但卻蘊含著機器學習中一些重要的基本思想。許多功能更為強大的非線性模型可線上性模型的基礎上通過引入層級結構或高維對映得到,因此瞭解線性模型對學習其他機器學習模型具有重要意義。 本文主要介紹機器學習中常用的線性模型,內
Numpy學習筆記(二):陣列的邏輯運算
在numpy中的邏輯運算: 與運算: vector = np.array([20,35,39,40]) equal_to_ten_and_five =(vector ==10)&(vector==5) print( equal_to_ten_and_fi
深度學習學習筆記(一):logistic regression與Gradient descent 2018.9.16
寫在開頭:這是本人學習吳恩達在網易雲課堂上的深度學習系列課程的學習筆記,僅供參考,歡迎交流學習! 一,先介紹了logistic regression,邏輯迴歸就是根據輸入預測一個值,這個值可能是0或者1,其影象是一條s形曲線,由預測值與真實值的差距計算出loss function損失函式和cos
Andrew NG 機器學習 筆記-week11-應用例項:圖片文字識別(Application Example:Photo OCR)
1、問題描述和流程圖(Problem Description and Pipeline) photo OCR:photo Optical Character Recognition 影象文字識別,要求從一張給定的圖片中識別文字。 為了完成這樣的工作,需
模式識別與機器學習筆記(二)機器學習的基礎理論
機器學習是一門對數學有很高要求的學科,在正式開始學習之前,我們需要掌握一定的數學理論,主要包括概率論、決策論、資訊理論。 一、極大似然估計(Maximam Likelihood Estimation,MLE ) 在瞭解極大似然估計之前,我們首先要明確什麼是似然函式(likelihoo
機器學習筆記(一):最小二乘法和梯度下降
一、最小二乘法 1.一元線性擬合的最小二乘法 先選取最為簡單的一元線性函式擬合助於我們理解最小二乘法的原理。 要讓一條直接最好的擬合紅色的資料點,那麼我們希望每個點到直線的殘差都最小。 設擬合直線為
機器學習筆記(二)線性迴歸實現
一、向量化 對於大量的求和運算,向量化思想往往能提高計算效率(利用線性代數運算庫),無論我們在使用MATLAB、Java等任何高階語言來編寫程式碼。 運算思想及程式碼對比 的同步更新過程向量化 向量化後的式子表示成為: 其中是一個向量,是一個實數,是一個向量,
機器學習筆記(十):TensorFlow實戰二(深層神經網路)
1 - 深度學習與深層神經網路 深度學習的精確定義為:“一類通過多層非線性變換對高複雜性資料建模演算法的集合” 因此,多層神經網路有著2個非常重要的特性 多層 非線性 1.1 - 線性模型的侷限性 線上性模型中,模型的輸出為輸入的加權和,假設一
機器學習筆記(二)吳恩達課程視訊
多元變數線性迴歸 1.多維特徵: 2.多元梯度下降: 代價函式:(目標與單變數一致,要找出使代價函式最小的一系列引數) 梯度下降演算法: 梯度下降演算法——特徵縮放: 除了固定以外,的值都要變成[-1,1]範圍左右之間的取值,不僅僅
機器學習筆記(二)
總結自 《機器學習》周志華 模型評估與選擇 錯誤率=樣本總數/分類錯誤的樣本數 精度=1-錯誤率 誤差:實際預測輸出與樣本真實輸出之間的差異 訓練誤差:學習器在訓練集上的誤差 泛化誤差:學習器在新樣本上的誤差 過擬合:學習能力過於強大,將訓練樣本本身的一些不太一
機器學習筆記(二)——分類器之優缺點分析
原始資料中存在著大量不完整、不一致、有異常的資料,須進行資料清洗。資料清洗主要是刪除原始資料集中的無關資料、重複資料,平滑噪聲資料,篩選掉與挖掘主題無關的資料,處理缺失值、異常值。 一、線性分類器: f=w^T+b / logistic regression 學習方
機器學習筆記(二)矩估計,極大似然估計
1.引數估計:矩估計 樣本統計量 設X1,X2…Xn…為一組樣本,則 - 樣本均值 : X¯¯¯=1n∑i=1nXi - 樣本方差:S2=1n−1∑i=1n(Xi−X¯¯¯
機器學習筆記(二)L1,L2正則化
2.正則化 2.1 什麼是正則化? (截自李航《統計學習方法》) 常用的正則項有L1,L2等,這裡只介紹這兩種。 2.2 L1正則項 L1正則,又稱lasso,其公式為: L1=α∑kj=1|θj| 特點:約束θj的大小,並且可以產
吳恩達機器學習筆記(二)(附程式設計作業連結)
吳恩達機器學習筆記(二) 標籤: 機器學習 一.邏輯迴歸(logistic regression) 1.邏輯函式&&S型函式(logistic function and sigmoid function) 線性迴歸的假設表示