一、定義
並查集是一種樹型的資料結構，用於處理一些不相交集合的合併及查詢問題。
基礎的並查集能實現以下三個操作：1.建立集合;2.查詢某個元素是否在一給定集合內（或查詢一個元素所在的集合）; 3.合併兩個集合.“並”“查”“集”三字由此而來。
並查集能解決的問題一般可以轉化為這樣的形式：初始時n個元素分屬不同的n個集合，通過不斷的給出元素間的聯絡，要求實時的統計元素間的關係（即是否存在直接或間接的聯絡）。
並查集本身不具有結構，可以用陣列、連結串列以及樹等實現。最常用的是陣列實現。

二、實現
陣列實現：
建立標記陣列father，用father[i]表示元素i所屬集合的標記。

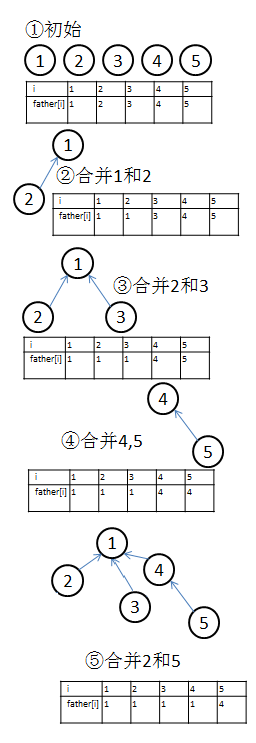圖示

1.建立集合 開始時每個元素各自獨立，可以把每個元素所屬集合標記為其自身序號。 void make() { int i; for(i=1;i<=n;i++) father[i]=i; } 2.合併集合&查詢元素所屬集合 find函式返回的是元素所屬集合的根結點（別忘了並查集是樹型的資料結構）。方法就是迴圈或遞迴，尋找當前結點的父結點，父結點的父結點，父結點的父結點的父結點......直到找到一個結點的父結點是它自己，那麼它就是根結點。 int find(int x)//非遞迴寫法 { while(father[x]!=x) x=father[x]; return x; } int find(int x)//遞迴寫法 { if(father[x])!=x) return find(father[x]); return x; } 因此，比較兩個元素x,y是否是同一集合的方法就是比較find(x)是否等於find(y)。 bool judge(int x,int y) { x=find(x); y=find(y); if(x==y) return true; else return false; } 合併集合的方法就是將其中一個點所在集合的根結點的父結點設定為另一個點所在集合的根結點。 void union1(int x,int y)//union是關鍵字，不能用，函式名可以隨便換一個方便的 { x=find(x); y=find(y); father[y]=x; }

前面的做法就是將元素的父親結點指來指去地指，當這棵樹是鏈的時候，可見判斷兩個元素是否屬於同一集合需要O(n)的時間。
舉個例子：在前面方法的第5步後,如果要查詢第3、5元素所在集合的根結點，那麼每次都需要查詢father[3](father[5])、father[2](father[4])、father[1]的值。
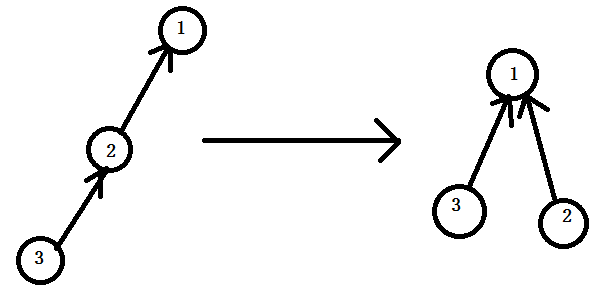
於是，路徑壓縮產生了作用。
路徑壓縮就是在找完根結點之後，在遞歸回來的時候順便把路徑上元素的父親結點都設為根結點。

int find(int x)//遞迴寫法
{
    if(father[x]!=x)
        father[x]=find(father[x]);
    return father[x];
}

int find(int x)//非遞迴寫法，不太好記但是更快，列幾組資料試一下也不難理解
{
	int r=x,q;
	while(r!=father[r])
		r=father[r];
	while(x!=r)
	{
		q=father[x];
		father[x]=r;
		x=q;
	}
	return r;
}

void make()
{
	int i;
	for(i=1;i<=n;i++)
	{
		father[i]=i;
		depth[i]=0;//如果初值為0則可以省略 
	}
}

void union1(int x,int y)
{
	int fx=find(x),fy=find(y);
	if(depth[fx]>depth[fy])
		father[fy]=fx;
	else
	{
		father[fx]=fy;
		if(depth[fx]==depth[fy])
			depth[fy]++;
	}
}