一、支援向量機（Support Vector Machines, SVM）

原理：找到離分隔超平面最近的點，確保它們離分隔平面的距離儘可能遠。

超平面（hyperplane）：決策的邊界，通常表示為 w.T*x+b=0，至於為何可以表示為一個平面，思考二維情況：

                                        w.T*x+b=0 即為 w1x1+w2x2+b=0，也就是平面座標系中的直線。

間隔（margin）：點到分隔平面的距離。

支援向量（Support Vector）：離分隔超平面最近的那些點。

分類器：

hw,b(x) = g(w.T*x+b)

若z≥0， g(z) = 1

若z<0，g(z) = -1

兩種距離表示：函式距離（functional margins）&幾何距離（geometric margins）

1. 函式距離： γ(i) = y(i)*(w.T*x(i)+b),    y(i)∈{-1, 1} （點(x(i), y(i))的函式距離）

當w.T*x+b>0時，y(i)=1，點離平面距離越遠，函式距離越大。

當w.T*x+b<0時，y(i)=-1，距離仍是一個很大的正數。

所以無論點在平面的正負側，函式距離都是正數，且距離越遠，數值越大。

定義某訓練集的函式距離為 γ = min i=1,...,m γ(i)  ,即訓練集中所有點的函式距離的最小值作為該訓練集的函式距離。

2. 幾何距離：γ(i) = y(i)*（(w/||w||).T*x(i) + b/||w||） （點(x(i), y(i))的幾何距離）

推導：

如圖，w為平面 w.T*x+b=0 的法向量（思考二維平面情況中，直線w1x1+w2x2+b=0的法向量為(w1, w2)，同理三維或N維）。

對於點A(x(i), y(i))來說，線段AB即是點A到超平面的幾何間隔，記為γ(i)。

所以B點的座標為：x(i) - γ(i)*w/||w||， w/||w||即為w向量方向上的單位向量。

又因為B點在超平面w.T*x+b=0上，所以滿足 w.T*(x(i) - γ(i)*w/||w||) + b = 0

可解得 γ(i) = (w/||w||).T*x(i)

再乘上y(i)保證符號，最後幾何間隔為： γ(i) = y(i)*（(w/||w||).T*x(i) + b/||w||）

同樣，定義訓練集的幾何間隔為 γ = min i=1,...,m γ(i)  ,即訓練集中所有點的幾何距離的最小值作為該訓練集的幾何距離。

在SVM優化問題中，我們選用幾何間隔而不是函式間隔，因為任意縮放參數(w, b)時，例如變為(2w, 2b)，hw,b(x)不改變，其只關心x的正負。但函式間隔改變，相當於×2，為使得函式具有任意縮放的性質，加入歸一化項，例如||w||，即使用幾何間隔。

回到SVM，根據目標：最大化支援向量到分隔面的距離，定義我們的原始優化問題為：

arg max w,b { min n (y(i)*(w.T*x(i)+b)) * 1/||w|| }

對乘積的優化很複雜，我們令所有支援向量的距離為1，即 y(i)*(w.T*x(i)+b) = 1，原始問題轉化為：

max w,b 1/||w||

s.t.  y(i)*(w.T*x(i)+b) ≥ 1 ,  i = 1,...,m

變換形式為：

min w,b 1/2||w||^2

s.t.  y(i)*(w.T*x(i)+b) ≥ 1 ,  i = 1,...,m

存在不等式約束的優化問題求解，我們使用拉格朗日數乘法，具體情況將在後面列出。

______________________________________________________________________________

二、對偶形式與KKT條件

該部分完全是為了求解SVM的優化問題做準備。

對於優化問題：

min f(x)

s.t. gi(x) ≤ 0,  i=1,...,k

構造拉格朗日函數：L（x, α）= f(x) + ∑αi*gi(x)

只有當αi ≥0 時，αi*gi(x) ≤ 0，所以 maxα L（x, α） = f(x)

∴ minx f(x) = minx maxα L（x, α）     (1)

∵ maxα minx L（x, α）= maxα [ minx f(x) + minx α*g(x) ] = maxα minx f(x) + maxα minx α*g(x) = minx f(x)  + maxα minx α*g(x)

∵ 當α=0或者g(x)=0時，minx α*g(x) = 0，否則 minx α*g(x) = -∞

∴ maxαminx α*g(x) = 0， 此時α=0或者g(x)=0

∴ maxα minx L（x, α）= minx f(x)     (2)

連線(1)和(2)：

minx maxα L（x, α） = maxα minx L（x, α）

稱左邊為原問題，右邊為原問題的對偶形式，即當滿足一定條件時，原問題的解與對偶問題的解相同，在最優解x*處，α=0或者g(x*)=0

所以KKT（Karush-Kuhn-Tucker）條件為：

（1） 拉格朗日函式對各引數求導=0

（2） αi ≥ 0

（3） αi*gi(x*) = 0

（4） gi(x*) ≤ 0   （原始約束條件）

KKT的含義其實是一組解成為最優解的必要條件。

——————————————————————————————————————————

三、求解SVM

回到SVM中，我們的優化問題為：

min w,b 1/2||w||^2

s.t.  y(i)*(w.T*x(i)+b) ≥ 1 ,  i = 1,...,m

構造拉格朗日函式：

L（w, b, α） = 1/2||w||^2 - ∑ αi*(y(i)*(w.T*x(i)+b)-1)

注意此處為了符合拉格朗日約束條件的形式，將原始約束條件轉化為≤。

即原始問題等於 minw,b maxα L(w, b, α)，由於滿足KKT條件，其對偶形式為maxα minw,b L(w, b, α)。

所以先根據拉格朗日函式對w,b分別求導，令導數等於0，得到：

w = ∑ αi y(i) x(i)

∑ αi y(i) = 0

將這兩個結果重新代入拉格朗日函式中，得到：

L（w, b, α） = ∑ αi - 1/2∑y(i)y(j)αiαj(x(i)).T*x(j)

即我們的優化問題變為：

maxα W(α) = ∑αi- 1/2∑y(i)y(j)αiαj(x(i)).T*x(j)

s.t. αi ≥ 0， i = 1,..., m

      ∑ αi y(i) = 0

這也是我們最終需要求解的問題，求出α後，可以得到w和b，以及分隔超平面 w.T*x+b=0。

該問題求解方法很多，通常使用SMO。

_____________________________________________________________________________

四、Kernel

對於有些問題，我們不希望直接使用原始輸入屬性（input attributes），例如輸入向量x為房屋區域長寬高之類，而我們通常使用面積、體積(?)來描述一個房子，使用x的平方或者立方來作為學習演算法的輸入。這些新獲得的輸入即特徵（features）。

我們用φ(x)來表示特徵對映，從原始輸入屬性到特徵的對映。如上面的問題可以表示為：

在SVM中，我們最終要求的問題是：

（word公式編輯器真是好用）

其中最後面這個可以換成φ(x)，即將原始屬性換種形式。

定義Kernel為：

我們將替換所有<x, z>為K(x, z)，將低維空間X對映到高維空間Z，使資料線性可分。

但通常Kernel計算開銷非常大，甚至φ(x)如果是個高維向量，其本身開銷也很大。（矩陣乘法時間複雜度為O(n^3)，橫向遍歷n^2，縱向遍歷n，當然有好的演算法可以降低到O(n^2.37)；對於向量，橫向遍歷N*1，縱向遍歷N，時間複雜度為O(n^2)）

我們可以直接用X空間表示Kernel，而不需要通過轉換為Z空間（花費O(n^2)）再計算內積。

例如：多項式Kernel：

可以寫為：

只需花費O(n)的時間來直接計算Kernel，（第一行，兩個括號中的公式可以同時運算，所以是O(n)），也就不需要顯示錶示出高維的φ(x)了。

相關Kernel也同理。

這就是kernel trick，即利用X空間的核函式計算，得到經過特徵轉換到Z空間的向量內積結果，即通過低維運算，得到高維轉換後的結果。

另外，我們知道，兩個垂直向量的內積為0，如果φ(x)和φ(z)距離較近，則核函式較大，反之如果較遠，或者說接近垂直，則核函式較小。所以核函式可以用來評估φ(x)和φ(z)的相似度，或者x與z的相似度。（比如高斯核函式，在0,1之間）

如何判斷某個函式是否為有效的Kernel?

首先定義Kernel matrix：

如果K是一個有效的Kernel，則有：

即矩陣K為對稱的。

另外可以推斷。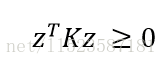

K是有效的核的充分必要條件是，矩陣K是對稱半正定矩陣。

五、正則化

在前面我們假設了資料集或者在低維或者在高維，資料線性可分，但通常會有一些異常值(outlier)使得分類器整個改變。如圖：

此類噪聲的影響，我們加入正則化，原始問題變為：

對於一些距離分類邊界1-ξ的樣本，我們增加了Cξ，確保了最小邊距為1。

然後構造拉格朗日函式：

得到最終對偶問題：

同時KKT條件有所改變：

正則化後的KKT條件推導：

上面的拉格朗日函式，分別對w和b求導，令導數=0。可以看到，對w求導，與正則化之前不變，仍得到

而對b求導則得到：

     這是一個很重要的結論。

同未正則化時的KKT推導一樣，

要想max L(w, b, ...) = f(x)，則需要後面兩項（不包括符號）最值為0，即≥0。此時：

要想對偶形式也等於minf(x)，則需要後兩項均為0。

 即以及，至於為什麼沒有求和符號，因為拉格朗日引數αi≥0，ri≥0，且ξi≥0，所以若想二者乘積和為0，則需要每個乘積都為0。

我們現在的條件有：

KKT為：

1. 當αi=0時，ri=C，則ξi=0，所以：

2. 同理，αi=C是，ri=0，自動滿足第三個條件；因為，ξi≥0，所以

3. 當0<αi<C，ri≠0，ξi=0，因為，所以

——————————————————————————————————————

六、SMO（sequential minimal optimization）

上文提到，求解最後對偶優化問題通常用SMO演算法。

我們先來看看座標上升法，即Coordinate ascent。

思考一個無約束優化問題：

座標上升演算法為：

在內迴圈中，每次固定除αi意外的變數，並將αi更改為函式取極值時的值。直到演算法收斂。

下圖是演算法迭代示意圖，每次更新都沿著座標軸方向，因為一次改變一個變數。

回到SMO，我們要解決的問題是：

如果我們使用座標上升法，一次改變一個αi，則將不滿足第二個約束條件。所以在SMO中，我們一次改變兩個α，演算法如下：

由於α有約束條件[0, C]，並且需要滿足在直線上，所以α取值範圍為[L, H]

最後α的更新應為：