2. 程式人生 > >svm原理詳細推導

svm原理詳細推導

阿新 • • 發佈：2018-11-17

筆者在查閱了大量資料和閱讀大佬的講解之後，終於對svm有了比較深一點的認識，先將理解的推導過程分享如下：

本文主要從如下五個方面進行介紹：基本推導，鬆弛因子，核函式，SMO演算法，小結五個方面以%%為分隔，同時有些地方需要解釋或者注意一下即在畫有---------符號的部分內。

本文主要介紹的是理論，並沒有涉及到程式碼，關於程式碼的具體實現，可以在閱讀完本文，掌握了SVM演算法的核心內容後去看一下筆者另一篇SVM程式碼剖析：

https://blog.csdn.net/weixin_42001089/article/details/83420109

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

基本推導

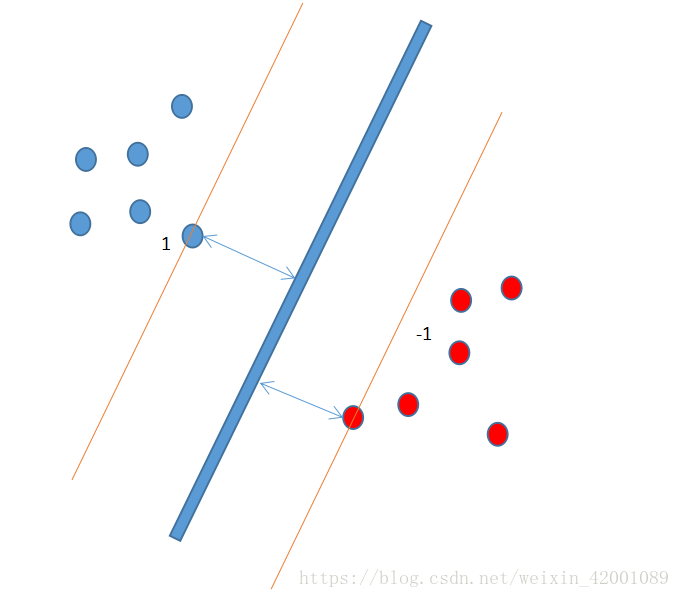
svm原理並不難理解，其可以歸結為一句話，就是最大化離超平面最近點（支援向量）到該平面的距離。

如下圖

開門見山就是下面的最值優化問題：

max_{w,b}(min_{x_{i}} \,\frac{y_{i}(w^{T}x_{i}+b)}{\left | w \right |} )

注意

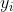（1）這裡的y_{i}就是標籤假設這裡是二分類問題，其值是1和-1，其保證了不論樣本屬於哪一類y_{i}(w^{T}x_{i}+b)都是大於0的

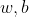（2）y_{i}(w^{T}x_{i}+b)稱為函式距離，,\frac{y_{i}(w^{T} x_{i}+b)}{\left | w\right |}稱為幾何距離，這裡之所以要使用幾何距離是因為，當w,b成倍增加時，函式距離也會相應的成倍的增加，而幾何函式則不會

這裡涉及到求兩個最值問題，比較棘手，正如上面所說，幾何距離不受成倍增加的影響，這裡不妨就將最近點到超平面的函式距離設為1，自然其他非最近點的函式距離便是大於1，於是以上問題轉化為：

\begin{matrix} max_{w,b} \, \frac{1}{\left | w \right |}\\ s.t \, \, \, y_{i}(wx_{i}+b)\geqslant 1 \end{matrix}\Rightarrow \begin{matrix} min_{w,b} \, \frac{1}{2}\left | w \right |^{2}\\ s.t \, \, \, y_{i}(wx_{i}+b)\geqslant 1 \end{matrix}

這是一個在有不等式約束下，最小值優化的問題，這裡可以使用kkt條件

--------------------------------------------------------------------------------------------------------------------------------------------------------------------

這裡簡單介紹一下kkt和拉格朗日乘子法（一般是用來求解最小值的優化問題的）

在求優化問題的時候，可以分為有約束和無約束兩種情況。

針對有約束的情況又有兩種情況即約束條件是等式或者是不等式

當是等式的時候：

\begin{matrix} min f(x)\\ s.t. \, g_{i}(x)=0 \, \, i=1,2,,,m\end{matrix}

首先寫出其拉格朗日函式：

\iota (x,\alpha )=f(x)+\sum_{i=1}^{m}\alpha _{i}g(x)\, \, (1)

需滿足的條件是：

\alpha _{i}\not\equiv 0

而當約束條件是不等式時，便可以使用kkt條件，其實kkt條件就是拉格朗日乘子法的泛化

\begin{matrix} minf(x)\\ s.t. \, g_{i}(x)=0\,\, \, \, i=1,2,,,m \\ h_{j}(x)\leqslant 0\, \, \, j=1,2,,,n \end{matrix}

同理首先寫出拉格朗日函式：

{\color{Magenta} \iota (x,\alpha ,\theta )=f(x)+\sum_{i=1}^{m}\alpha _{i}g_{i}(x)+\sum_{j=1}^{n}\theta _{i}h_{i}(x)\, \, \, \, (2)}

好了，接著往下走介紹拉格朗日對偶性：

上面問題可以轉化為（稱為原始問題）：

min_{x}\, max_{\alpha ,\theta }\iota (x,\alpha ,\theta )

為什麼可以轉化呢？這裡是最難理解的：筆者還沒有完全透徹的理解，這裡試著解釋一下吧，也是網上最流行的解釋方法：

這裡分兩種情況進行討論：

當g(x)或者h(x)不滿足約束條件時：

那麼顯然：max_{\alpha ,\theta }(x,\alpha ,\theta )=+\infty因為當h(x)>0時我們可令\theta =+\infty,g(x)\not\equiv 0時我們令\alpha =-\infty或者\alpha =+\infty

當g(x)或者h(x)滿足約束條件時：

max_{\alpha ,\theta }(x,\alpha ,\theta )=f(x)

綜上所述：

max_{\alpha ,\theta }(x,\alpha ,\theta )=\begin{pmatrix} f(x)\, \, \, \, \, \, \, \, \, \, g(x)\, and \, \, h(x) satisfy\, constraints\\ +\infty \, \, \, \, \, \, \, \, \, others \end{pmatrix}

所以如果考慮極小值問題那麼就可以轉化為：

min_{x}\, max_{\alpha ,\theta }\iota (x,\alpha ,\theta )

還有一種比較直觀的方法，這裡不再證明，可以參考：https://www.zhihu.com/question/58584814/answer/159863739第二個回答

對偶問題：

上面關於拉格朗日最小最大值問題可以轉化為求其對偶問題解決：

{\color{Magenta} {\color{Magenta} }{\color{Orchid} }max_{\alpha ,\theta }\, min_{x}\, \iota (x,\alpha ,\theta )}

兩者關係：

假設原始問題的最優解是p^{*},其對偶問題的最優解是d^{*},那麼容易得到：

min_{x}\, \, \iota (x,\alpha ,\theta )\leq \iota (x,\alpha ,\theta )\leqslant max_{\alpha ,\theta }\, \iota (x,\alpha ,\theta )\Rightarrow max_{\alpha ,\theta }\, min_{x}\, \iota (x,\alpha ,\theta )\, \leq min_{x}\, max_{\alpha ,\theta }\iota (x,\alpha ,\theta )\Rightarrow d^{*}\leq p^{*}

即其對偶問題的解小於等於原始問題的解，現在我們要通過其對偶問題來求的原始問題的解對吧，所以我們希望的是d^{*}= p^{*}

那麼什麼時候才能相等呢？這就必須滿足的kkt條件：

{\color{Magenta} \left\{\begin{matrix} \frac{\partial \iota (x,\alpha ,\theta )}{\partial x}| _{x=x^{*}}=0\\ \frac{\partial \iota (x,\alpha ,\theta )}{\partial \alpha }|_{x=x^{*}}=0\\ \frac{\partial \iota (x,\alpha ,\theta )}{\partial \theta }|_{x=x^{*}}=0\\ \alpha _{i}\neq 0 \\ \theta _{j}\geqslant 0 \\ \theta _{j}h_{j}(x)|_{x=x^{*}}=0 \\ h_{j}(x)|_{x=x^{*}}\leq 0 \\ g_{i}(x)|_{x=x^{*}}=0 \end{matrix}\right.}

-----------------------------------------------------------------------------------------------------------------------------------------------------------------

說了這麼多拉格朗日的東西，其實其本質作用就是，將有不等式約束問題轉化為無約束問題（極小極大值問題），然後又進一步在滿足kkt條件下將問題轉化為了其對偶問題，使之更容易求解，下面要用到的就是上面紫色的部分，關於更深的拉格朗日求解問題大家可以去收集資料參看。

對應到SVM的拉格朗日函式便是：

\iota (w,b,\alpha )=\frac{1}{2}\left | w \right |^{2}{\color{Red} -}\sum_{i=1}^{m}\alpha _{i}\left [ y_{i}(w^{T}x_{i}+b)-1 \right ]

-----------------------------------------------------------------------------------------------------------------------------------------------------------

注意上面給的不等式約束是h_{j}(x)\leq 0即小於等於，而這裡的不等式約束是大於等於所以紅色部分是減法

----------------------------------------------------------------------------------------------------------------------------------------------------------

於是問題轉化為：

min_{w,b} \, \, (max_{\alpha }(\iota (w,b,\alpha )))

根據對偶轉化：

max_{\alpha } \, \, (min_{w,b }(\iota (w,b,\alpha )))

好啦，這裡沒什麼說的就是根據kkt條件求偏導令其為0：

\begin{matrix} \frac{\partial \iota (w,b,\alpha )}{\partial w}=w-\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}=0\\\frac{\partial\iota (w,b,\alpha) }{\partial b}=\sum_{i=1}^{m}\alpha _{i}y_{i}=0\end{matrix}

於是就得到：

\begin{matrix} w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}\\ \sum_{i=1}^{m}\alpha _{i}y_{i}=0 \end{matrix}

將上述兩公式帶入到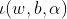\iota (w,b,\alpha )如下：

\iota (w,b,\alpha )=\frac{1}{2}w^{T}w-\sum_{i=1}^{m}\alpha _{i}y_{i}w^{T}x_{i}-b\sum_{i=1}^{m}\alpha _{i}y_{i}+\sum_{i=1}^{m}\alpha _{i}=\frac{1}{2}w^{T}w-\sum_{i=1}^{m}\alpha _{i}y_{i}w^{T}x_{i}+\sum_{i=1}^{m}\alpha _{i}=\frac{1}{2}w^{T}\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}-w^{T}\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}+\sum_{i=1}^{m}\alpha _{i}=\sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}w^{T}\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}=\sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}

於是問題轉化為：

\begin{matrix} max_{\alpha }\, \, \sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}\\ s.t. \, \, \alpha _{i}\geqslant 0 \\ \sum_{i=1}^{m}\alpha _{i}y_{i}=0 \end{matrix}

所以最後就得出這樣的步驟：

1首先根據上面的最優化問題求出一些列的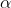\alpha

 

2然後求出w和b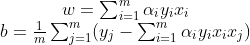\begin{matrix} w=\sum_{i=1}^{m}\alpha_{i} y_{i}x_{i}\\b=\frac{1}{m}\sum_{j=1}^{m}(y_{j} -\sum_{i=1}^{m}\alpha_{i} y_{i}x_{i}x_{j})\end{matrix}

所以當一個樣本進來的時候即值便是：

y=\sum_{i=1}^{m}\alpha_{i} y_{i}x_{i}x+\frac{1}{m}\sum_{j=1}^{m}(y_{j} -\sum_{i=1}^{m}\alpha_{i} y_{i}x_{i}x_{j})

3根據如下進行分類：

sign(y)

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

鬆弛因子

上面是SVM最基本的推導，下面說一下這種情況就是有一個點由於採集錯誤或者其他原因，導致其位置落在了別的離別當中，而svm是找最近的點，所以這時候找出的超平面就會過擬合，解決的辦法就是忽略掉這些點（離群點），即假如鬆弛因子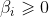\beta _{i}\geqslant 0,使幾何距離不那麼大於1

數學化後的約束條件即變為：

min_{w,b,\beta } \, (\frac{1}{2}\left | w \right |^{2}+C\sum_{i=1}^{m}\beta_{i}) \\ s.t \, \, \, y_{i}(w^{T}x_{i}+b)\geqslant 1-\beta _{i}\\\beta _{i}\geq 0

這裡簡單來理解一些C的含義：這是一個在使用SVM時需要調的引數，\beta代表離群點到底離群點有多遠，而C就是我們對這些點的重視程度，假設現在\sum_{i=1}^{m}\beta_{i}是一個定值，那麼當C越大，就代表我們越重視這些點，越不想捨棄這些點，即極端的當C=+\infty時，優化是求min，則無解，即對應的直觀理解就是：這時線性不可分，大家都混在一起，這時又不想捨棄任何一個點，自然就不能找到適合的超平面（當然可以使用核函式進行對映分類，後面說明）

接下來還是使用上面拉格朗日對偶問題進行求解，這裡就不詳細說明了，直接給出過程：

\begin{matrix} min_{w,b,\beta }\, \, \, max_{\alpha ,\gamma }(\frac{1}{2}|w|^{2}+C\sum_{i=1}^{m}\beta _{i}-\sum_{i=1}^{m}\alpha _{i}(y_{i}(wx_{i}+b)-1+\beta _{i})-\sum_{j=1}^{m}\gamma _{j}\beta _{j})\\ {\color{Red} \Rightarrow }\\ max_{\alpha ,\gamma }\, \, \, min_{w,b,\beta }(\frac{1}{2}|w|^{2}+C\sum_{i=1}^{m}\beta _{i}-\sum_{i=1}^{m}\alpha _{i}(y_{i}(wx_{i}+b)-1+\beta _{i})-\sum_{j=1}^{m}\gamma _{j}\beta _{j}) \end{matrix}

令

\iota (w,b,\beta ,\alpha ,\gamma )=\frac{1}{2}|w|^{2}+C\sum_{i=1}^{m}\beta _{i}-\sum_{i=1}^{m}\alpha _{i}(y_{i}(wx_{i}+b)-1+\beta _{i})-\sum_{j=1}^{m}\gamma _{j}\beta _{j}

求導令其為0：

\frac{\partial \iota (w,b,\beta ,\alpha ,\gamma )}{\partial w}=w-\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}=0\Rightarrow w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}

\frac{\partial \iota (w,b,\beta ,\alpha ,\gamma )}{\partial b}=-\sum_{i=1}^{m}\alpha _{i}y_{i}=0\Rightarrow \sum_{i=1}^{m}\alpha _{i}y_{i}=0

\frac{\partial \iota (w,b,\beta ,\alpha ,\gamma )}{\partial \beta }=0\Rightarrow C-\alpha _{i}-\gamma _{i}=0

將其帶入最終問題可得：

max_{\alpha }\, \, \sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}

---------------------------------------------------------------------------------------------------------------------------------------------------------------------

這裡得到的和沒加鬆弛變數時是一樣的

------------------------------------------------------------------------------------------------------------------------------------------------

對應的kkt條件為：

\sum_{i=1}^{m}\alpha _{i}y_{i}=0 \, \, \, (1)

\alpha _{i}\left [ y_{i}y(x) -(1-\beta _{i})\right ]=0\, \, \, \, (2)

\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\, \, \, \, (3)

\gamma _{i}\beta _{i}=0\, \, (4)

\beta _{i}\geq 0\, \, \, (5)

\alpha _{i}\geq 0\, \, \, (6)

\gamma _{i}\geq 0\, \, \, (7)

C-\alpha _{i}-\gamma _{i}=0\, \, \, (8)

w=\sum_{i=1}^{m}\alpha _{i}y_{i}x_{i}\, \, \, \, (9)

注意如下幾點：

一：對比最開始的kkt條件模板

{\color{Magenta} \left\{\begin{matrix} \frac{\partial \iota (x,\alpha ,\theta )}{\partial x}| _{x=x^{*}}=0\\ \frac{\partial \iota (x,\alpha ,\theta )}{\partial \alpha }|_{x=x^{*}}=0\\ \frac{\partial \iota (x,\alpha ,\theta )}{\partial \theta }|_{x=x^{*}}=0\\ \alpha _{i}\neq 0 \\ \theta _{j}\geqslant 0 \\ \theta _{j}h_{j}(x)|_{x=x^{*}}=0 \\ h_{j}(x)|_{x=x^{*}}\leq 0 \\ g_{i}(x)|_{x=x^{*}}=0 \end{matrix}\right.}

這裡的(1)(8)(9)是求偏導的結果即一二三公式，(6)(7)是拉格朗日乘子即相當於模板的第五公式，(2)(4)相當於模板第六個公式，(3)(5)是原始約束條件即相當於模板的第七個公式

二：可以將kkt中部分條件進行總結歸納：（6）（7）（8）三個條件：

\begin{matrix} \gamma _{i}=C-\alpha _{i}\\ \gamma _{i}\geq 0 \end{matrix}\Rightarrow C-\alpha _{i}\geq 0\Rightarrow \alpha _{i}\leq C

\begin{matrix} \alpha _{i}\leq C\\ \alpha _{i}\geq 0 \end{matrix}\Rightarrow 0\leq \alpha _{i}\leq C

所以可以總結為：

\begin{matrix} max_{\alpha }\, \, \sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}\\ s.t. \, \, \sum_{i=1}^{m}\alpha _{i}y_{i}=0 \\ 0\leq \alpha _{i}\leq C \end{matrix}

可以看到這裡和沒加鬆弛變數相比，唯一不同的就是{\color{Red} \alpha }有了上界C，它代表著我們對那些離群點的重視程度

三：說一下\alpha _{i}取不同值時意義

對比模板

當\theta _{i}^{*}> 0時，對應的h_{i}(x^{*})=0即x^{*}邊界點

當\theta _{i}^{*}= 0時，對應的h_{i}(x^{*})< 0即x^{*}非邊界點

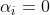當\alpha _{i}=0時：

由（8）可得：C-\alpha _{i}-\gamma _{i}=0\Rightarrow \gamma _{i}=C\Rightarrow \gamma _{i}> 0

又有公式（4）可得：\begin{pmatrix} \gamma _{i}> 0\\\gamma _{i}\beta _{i}=0 \end{pmatrix}\Rightarrow \beta _{i}=0

最後又公式（3）可得：\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\Rightarrow y_{i}y(x) \geq 1

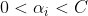當0< \alpha _{i}< C時：

C-\alpha _{i}-\gamma _{i}=0\Rightarrow \gamma _{i}=C-\alpha _{i}\Rightarrow \gamma _{i}> 0

同理\begin{pmatrix} \gamma _{i}> 0\\\gamma _{i}\beta _{i}=0 \end{pmatrix}\Rightarrow \beta _{i}=0

又（2）可得：

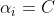\begin{pmatrix} \alpha _{i}\left [ y_{i}y(x) -(1-\beta _{i})\right ]=0\\ 0< \alpha _{i}< C \end{pmatrix}\Rightarrow \left [ y_{i}y(x) -(1-\beta _{i})\right ]=0

最後：

\begin{pmatrix} y_{i}y(x) =(1-\beta _{i})\\ \beta _{i}=0 \end{pmatrix}\Rightarrow y_{i}y(x) =1

當\alpha _{i}= C時：

C-\alpha _{i}-\gamma _{i}=0\Rightarrow \gamma _{i}=0

進而這裡還是隻能得到\beta _{i}\geq 0即\begin{matrix} \gamma _{i}=0\\ \gamma _{i}\beta _{i}= 0 \\ \beta _{i} \geq 0\end{matrix}\Rightarrow \beta _{i} \geq 0

\left [ y_{i}y(x) -(1-\beta _{i})\right ]\geq 0\Rightarrow y_{i}y(x) \geq (1-\beta _{i})

最後：

\begin{pmatrix} y_{i}y(x) \geq (1-\beta _{i})\\ \beta _{i}\geq 0 \end{pmatrix}\Rightarrow y_{i}y(x) \leq 1

綜上所述可以總結為：

\begin{matrix} \alpha _{i}=0\Leftrightarrow y_{i}y(x)\geq 1\\ 0< \alpha _{i}< C\Leftrightarrow y_{i}y(x)= 1 \\ \alpha _{i}=C\Leftrightarrow y_{i}y(x)\leq 1 \end{matrix}

在點在兩條間隔線外則，對應前面的係數\alpha為0，在兩條間隔線裡面的對應的係數為C，在兩條間隔線上的點對應的係數在0和C之間。

通過上面也可以看出，最後求出的所有\alpha按理說為0的居多，畢竟大部分資料點應該是在間隔線外的對吧。

所以對應到鬆弛遍歷這裡的步驟就是：

1首先根據上面的最優化問題求出一些列的\alpha

 

2然後求出w和b \begin{matrix} w=\sum_{i=1}^{m}\alpha_{i} y_{i}x_{i}\\b=\frac{min_{i:y=1}w^{*}x_{i}+max_{i:y=-1}w^{*}x_{i}}{2}\end{matrix}

注意這裡是隨便取一個點i就可以算出b，但是實際中往往取所有點的平均

 

3得出超平面

注意這裡說一下\alpha _{i}的意義，由前面基本推導的kkt部分討論可知：

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

核函式：

出現的背景：

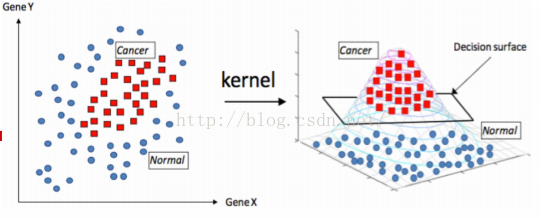
對於一些線性不可分的情況，比如一些資料混合在一起，我們可以將資料先對映到高緯，然後在使用svm找到當前高緯度的超平面，進而將資料進行有效的分離，一個直觀的例子：

圖片來源七月演算法

比如原來是：

y=\sum_{i=1}^{m}\alpha _{i}^{*}y_{i}x_{i}x+b

則現在為：

y=\sum_{i=1}^{m}\alpha _{i}^{*}y_{i}\Phi (x_{i})\Phi (x)+b\Rightarrow \sum_{i=1}^{m}\alpha _{i}^{*}y_{i}< \Phi (x_{i})\Phi (x)> +b

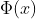其中\Phi (x)就是對映公式，即先對映到高緯再進行內積

但是問題來了，那就是假設原始資料維度就好高，再進一步對映到高緯，那麼最後的維度可能就非常之高，再進行內積等這一系列計算要求太高，很難計算。

因此我們可以令

\sum_{i=1}^{m}\alpha _{i}^{*}y_{i}< \Phi (x_{i})\Phi (x)> +b\Rightarrow \sum_{i=1}^{m}\alpha _{i}^{*}y_{i} \, \, K<x_{i},x> +b

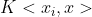這裡的K< x_{i},x>便是核函式，其意義在於我們不用去對映到高緯再內積，而是直接在低緯使用一種核函式計算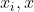x_{i},x,使其結果和對映到高緯再內積效果一樣，這就是核函式的威力，大部分是內積，而SVM的奇妙之處就在於所有的運算都可以寫成內積的形式，但是這種核函式具體該怎麼選取呢？別慌，已經有前輩們幫我們找到了很多核函式，我們直接拿過來用就可以啦。

下面介紹幾種常見的吧：更多的大家可以自行查閱：

(1)線性核函式 :也是首選的用來測試效果的核函式
K(x_{i},x)=x_{i}\cdot x
其維度與原來相同，主要用於線性可分的情況，其實就是原始匯出的結果
(2)多項式核函式 

K(x_{i},x)=[(x_{i}\cdot x)+1]^{m}
其實現將低維的輸入空間對映到高緯的特徵空間，但多項式的階數也不能太高，否則核矩陣的元素值將趨於無窮大或者無窮小，計算複雜度同樣會大到無法計算。而且它還有一個缺點就是超引數過多
(3)徑向基高斯（RBF）核函式 
K(x_{i},x)=exp(-\frac{\left \| x_{i}-x \right \|^{2}}{2\delta ^{2}})
高斯（RBF）核函式核函式效能較好，適用於各種規模的資料點，而且引數要少，因此大多數情況下優先使用高斯核函式。
(4)sigmoid核函式 

K(x_{i},x)=tanh(\eta < x_{i},x> +\theta )
不難看出這裡有點深度學習當中，一個簡單的神經網路層

總的來說就是，當樣本足夠多時，維度也足夠高即本身維度已經滿足線性可分，那麼可以考慮使用線性核函式，當樣本足夠多但是維度不高時，可以考慮認為的增加一定的維度，再使用線性核函式，當樣本也不多，維度也不高時，這時候可以考慮使用高斯（RBF）核函式。

關於SVM ，python中有一個機器學習庫sklearn，其中集成了很多機器學習方法，包括SVM，筆者這裡也做過一個簡單直觀的呼叫，可以參看https://blog.csdn.net/weixin_42001089/article/details/79952399

再者就是我們雖然可以直接拿sklearn庫下整合好的介面來用，但是其具體實現細節，還是有必要了解一下，換句話說：

上面我們最後得到的結果是：

\begin{matrix} max_{\alpha }\, \, \sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}\\ s.t. \, \, \sum_{i=1}^{m}\alpha _{i}y_{i}=0 \\ 0\leq \alpha _{i}\leq C \end{matrix}

我們求出一些列\alpha便可，可是\alpha具體怎麼求呢？落實到程式碼上面應該怎麼搞呢？下面就來說說這個事情
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

SMO演算法

現在的問題是：

\begin{matrix} max_{\alpha }\, \, \sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}\\ s.t. \, \, \sum_{i=1}^{m}\alpha _{i}y_{i}=0 \\ 0\leq \alpha _{i}\leq C \end{matrix}

首先要明確我們的目的是求一些列的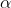\alpha，其思路也是很簡單就是固定一個引數即以此為自變數，然後將其他的變數看成常數，只不過因為這裡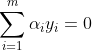\sum_{i=1}^{m}\alpha _{i}y_{i}=0約束條件，所以我們一次取出兩個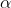\alpha作為自變數進行優化，然後外面就是一個大的迴圈，不停的取不停的優化，知道達到某個條件（後面介紹）停止優化。

思路框架就是上面這麼簡單，下面來看一下理論方面的精確推導：

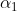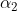假設我們首先取出了\alpha _{1}和\alpha _{2},那麼後面的便可以整體視為一個常數即：

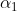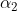\alpha _{1}y_{1}+\alpha _{2}y_{2} = -\sum_{i=3}^{m}\alpha _{i}y_{i}\Rightarrow \alpha _{1}y_{1}+\alpha _{2}y_{2} =\zeta

先將\alpha _{1}用\alpha _{2}表示出來，也很簡單：

\alpha _{1}=(\zeta-\alpha _{2}y_{2})y_{1}

帶入到原始優化的目標方程中可得：

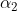\sum_{i=1}^{m}\alpha _{i}-\frac{1}{2}\sum_{i,j=1}^{m}\alpha _{i}\alpha _{j}y_{i}y_{j}x_{i}x_{j}=a\alpha _{2}^{2}+b\alpha _{2}+c

即關於\alpha _{2}的一元二次方程（其中a,b,c都是常數）

--------------------------------------------------------------------------------------------------------------------------------------------------------------

為什麼是二元一次方程呢？很簡單由原始優化目標可以看出基本單元就是\alpha _{i}\alpha _{j},然後就是組合相加，所以最高次數就是2次，前面還有單次項，後面有常數項，所以最後歸結起來就是一個一元二次方程

-------------------------------------------------------------------------------------------------------------------------------------------------------------

好啦，求一元二次方程最值應該很簡單啦吧，即：

\alpha _{2}=-\frac{b}{2a}

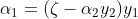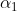
相應的根據\alpha _{1}=(\zeta-\alpha _{2}y_{2})y_{1}便可以求出\alpha _{1}

這樣就完成啦一對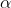\alpha值的優化，接著找下一對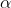\alpha值就行優化即可

-------------------------------------------------------------------------------------------------------------------------------------------------------------

介紹到這裡也許會發現還有一個約束條件沒有用即：

0\leq \alpha _{i}\leq C

是的我們在算\alpha _{1}\alpha _{2}的時候，最後還應該加一步就是將其值約束到[0,C]

回到：

\alpha _{1}y_{1}+\alpha _{2}y_{2} =\zeta

我們分類討論：

（1）當y_{1}和y_{2}是同號時：

則是一個斜率為-1的直線即\alpha _{1}+\alpha _{2}=\$

那麼可以畫出如下圖。橫座標是\alpha _{1}，縱座標是\alpha _{2}，可以看到直線有如下兩種情況

現在要保證範圍，即\alpha _{2}的最大值在兩種情況下分別是\$和C，最小值分別是0和\$ -C

所以最後綜合一下即

\begin{matrix} L=max(0,\$ -C)=max(0,\alpha _{1}+\alpha _{2}-C)\\ H=min(\$ ,C)=min(\alpha _{1}+\alpha _{2},C)\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \end{matrix}

（2）噹噹y_{1}和y_{2}是異號時：

則是一個斜率為1的直線即\alpha _{1}-\alpha _{2}=\$

那麼可以畫出如下圖。橫座標是\alpha _{1}，縱座標是\alpha _{2}，可以看到直線有如下兩種情況

現在要保證範圍，即\alpha _{2}的最大值在兩種情況下分別是C-\$和C，最小值分別是0和-\$

所以最後綜合一下即

\begin{matrix} L=max(0,-\$ )=max(0,\alpha _{2}-\alpha _{1})\\ H=min(C-\$ ,C)=min(C-\alpha _{1}+\alpha _{2},C) \end{matrix}

所以在我們通過一元二次方程求得的\alpha _{2}並不是最終的\alpha _{2}而是經過以下：

\alpha ^{*}_{2}=\begin{Bmatrix} L\, \,\, \, \, \, \, \, \, \, \, \, if \, \, \, \,\alpha _{2}<L\\ \alpha _{2}\, \,\, \, \, \, \, \, \, \, if \, \, \, L\leq \alpha _{2}\leqslant H\\ H\,\, \, \, \, \, \, \, \, \, \, \, if \, \, \alpha _{2}> H \end{Bmatrix}

注意這裡有時候L=H這代表\alpha _{1},\alpha _{2}都在邊界（值等於0或者C）則不用對這一對\alpha進行優化啦，因為他們已經在邊界啦，因此不再能夠減少或者增大（其值太大會被強行賦值為H，同理太小為L），因此也就不值得再對他們進行優化啦，直接跳過尋找下一對需要優化的\alpha對即可

--------------------------------------------------------------------------------------------------------------------------------------------------------------

好的我們接著往下走，剛才說得到一個一元二次方程組那麼係數a,b,c是多少呢？我們來求一下：

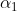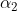我們先將\alpha _{1}和\alpha _{2}帶入：

公式太多就不用編輯器啦，字跡有點潦草==

現在我們進一步化簡一下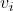v_{i}:

我們將本次要優化的引數標為*即規範一下就是：

相對應v_{i}中的\alpha沒有*就代表使用上次結果的\alpha

相關推薦

svm原理詳細推導

筆者在查閱了大量資料和閱讀大佬的講解之後，終於對svm有了比較深一點的認識，先將理解的推導過程分享如下： 本文主要從如下五個方面進行介紹：基本推導，鬆弛因子，核函式，SMO演算法，小結五個方面以%%為分隔，同時有些地方需要解釋或者注意一下即在畫有---------符號的部分內。 本文主要介紹

機器學習筆記之十二——SVM原理及推導

svm（support vector machine）是一種二分類演算法，它的目標在於尋找一個能將兩種點分離的直線或平面或超平面。 如圖（來自wiki）： 圖中的紅線將兩邊資料點分開，這條線就是分割直線，同樣的，在三維座標軸中，將兩邊資料點分開的平面，稱為分割平面；更高維的空間座標軸，

【機器學習】支援向量機SVM原理及推導

參考：http://blog.csdn.net/ajianyingxiaoqinghan/article/details/72897399 部分圖片來自於上面部落格。 0 由來 在二分類問題中，我們可以計算資料代入模型後得到的結果，如果這個結果有明顯的區別，

動態規劃之揹包問題原理詳細推導及其實現

貪心演算法：（1）      給定n個物品，物品價值分別為P1，P2，…，Pn，物品重量分別W1，W2, …, Wn，揹包容量為M。每種物品可部分裝入到揹包中。輸出X1，X2，…，Xn，0<Xi<1, 使得

【機器學習】演算法原理詳細推導與實現(一):線性迴歸

【機器學習】演算法原理詳細推導與實現(一):線性迴歸 今天我們這裡要講第一個有監督學習演算法，他可以用於一個迴歸任務，這個演算法叫做 線性迴歸 房價預測 假設存在如下 m 組房價資料： 面積(m^2) 價格(萬元) 82.35 193 65.00 213 114.20 255 75.

【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸

【機器學習】演算法原理詳細推導與實現(二):邏輯迴歸 在上一篇演算法中，線性迴歸實際上是 連續型 的結果，即 \(y\in R\) ，而邏輯迴歸的 \(y\) 是離散型，只能取兩個值 \(y\in \{0,1\}\)，這可以用來處理一些分類的問題。 logistic函式 我們可能會遇到一些分類問題，例如想要劃

【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯

【機器學習】演算法原理詳細推導與實現(三):樸素貝葉斯 在上一篇演算法中，邏輯迴歸作為一種二分類的分類器，一般的迴歸模型也是是判別模型，也就根據特徵值來求結果概率。形式化表示為 \(p(y|x;\theta)\)，在引數 \(\theta\) 確定的情況下，求解條件概率 \(p(y|x)\) 。通俗的解釋為：

【機器學習】演算法原理詳細推導與實現(四):支援向量機(上)

【機器學習】演算法原理詳細推導與實現(四):支援向量機(上) 在之前的文章中，包括線性迴歸和邏輯迴歸，都是以線性分界線進行分割劃分種類的。而本次介紹一種很強的分類器【支援向量機】，它適用於線性和非線性分界線的分類方法。 函式間隔概念 為了更好的理解非線性分界線，區別兩種分界線對於分類的直觀理解，第一種直觀理解

【機器學習】演算法原理詳細推導與實現(五):支援向量機(下)

【機器學習】演算法原理詳細推導與實現(五):支援向量機(下) 上一章節介紹了支援向量機的生成和求解方式，能夠根據訓練集依次得出\(\omega\)、\(b\)的計算方式，但是如何求解需要用到核函式，將在這一章詳細推導實現。 核函式 在講核函式之前，要對上一章節得到的結果列舉出來。之前需要優化的凸函式為： \[

【機器學習】演算法原理詳細推導與實現(六):k-means演算法

【機器學習】演算法原理詳細推導與實現(六):k-means演算法 之前幾個章節都是介紹有監督學習，這個章節介紹無監督學習，這是一個被稱為k-means的聚類演算法，也叫做k均值聚類演算法。 聚類演算法 在講監督學習的時候，通常會畫這樣一張圖： 這時候需要用logistic迴歸或者SVM將這些資料分成正負兩

【機器學習】演算法原理詳細推導與實現(七):決策樹演算法

# 【機器學習】演算法原理詳細推導與實現(七):決策樹演算法 在之前的文章中，對於介紹的分類演算法有[邏輯迴歸演算法](https://www.cnblogs.com/TTyb/p/10976291.html)和[樸素貝葉斯演算法](https://www.cnblogs.com/TTyb/p/109890

【支援向量機SVM】 演算法原理 公式推導 python程式設計實現

1.前言     如圖，對於一個給定的資料集，通過直線A或直線B（多維座標系中為平面A或平面B）可以較好的將紅點與藍點分類。那麼線A與線B那個更優呢？                   在SVM演算法中，我們認為線A是優於線B的。因為A的‘分類間隔’大於B。

支援向量機SVM(直觀理解原理、推導)

這裡主要基於吳恩達機器學習課程對於SVM的講解進行總結回顧，並參考各類資料對其推導過程進一步理解及實現。所以分為兩個部分及最後的一些個人總結。(內容較多、篇幅較長，靜下心來、慢慢體會) 第一部分也即吳恩達課程是從邏輯迴歸的cost函式講到svm的cost優化問題

(3).支援向量機SVM——軟間隔最大化公式手寫詳細推導

線性可分問題的支援向量機學習方法，對線性不可分訓練資料是不適應的，因為這時上一節中不等式約束不能成立，如何擴充套件到線性不可分問題呢？這就需要修改硬間隔最大化，使其成為軟間隔最大化。 通常情況下訓練資料中有一些特異的點，將這些特異的點去處後，剩下的樣本組成的集合是線性可分的。線性不可分的意思

SVM的原理及推導

SVM的原理及推導 我們直接用數學公式來描述我們要解決的問題。假設我有一個數據集 D \mathcal{D}

SVM原理、公式推導、libsvm原始碼分析

恰好翻到了以前記的cs229的筆記, 其實也想了好久要不要跟風去推導公式, 寫寫就當是複習一下了 說到svm, 按套路就要先說說線性分類器, 如圖, 在特徵維數為2時, 可以用一條線將正負樣本分離開

SVM原理推導以及SMO、Kernel的理解

一、支援向量機（Support Vector Machines, SVM）原理：找到離分隔超平面最近的點，確保它們離分隔平面的距離儘可能遠。超平面（hyperplane）：決策的邊界，通常表示為 w.T*x+b=0，至於為何可以表示為一個平面，思考二維情況：         

【SVM】原理和推導1

參考部落格：https://blog.csdn.net/szlcw1/article/details/52259668https://www.jianshu.com/p/f4c7bc6c4ce21.線性可分SVM2.線性SVM

支持向量機（SVM）之數學公式詳細推導

數學推導 技術分享 machine 使用 數據線 手寫筆 形式 支持 tor 一、【概述】 1、含義： 支持向量機（support vector machine，SVM）是一種二類分類器，它的基本模型是定義在特征空間上的間隔最大化的線性分類器，通過引入核函數，也可以作為

機器學習 | 深入SVM原理及模型推導（一）

本文始發於個人公眾號：**TechFlow**，原創不易，求個關注 今天是**機器學習專題**的第32篇文章，我們來聊聊SVM。 SVM模型大家可能非常熟悉，可能都知道它是面試的常客，經常被問到。它最早誕生於上世紀六十年代。那時候雖然沒有機器學習的概念，也沒有這麼強的計算能力，但是相關的模型和理論已經