本文是基於吳恩達老師《深度學習》第二週第一課練習題所做，目的在於探究引數初始化對模型精度的影響。

一、資料處理

本文所用第三方庫如下，其中reg_utils 和 testCases_regularization為輔助程式從這裡下載。

import numpy as np
import matplotlib.pyplot as plt
from reg_utils import *
import sklearn
import sklearn.datasets
import scipy.io
from testCases_regularization import *

本次課程中使用了一個比較有趣的例子：使用人工智慧的方法為一支足球隊做技術分析，為隊員預測頭球破門率最高的位置。

下圖給出了過去十場比賽中，該隊與對手搶得頭球點的資料集

藍色點表示本隊搶到頭球時隊員所在的位置，紅點表示對手搶到頭球時所在的位置。本文的任務是建立深層神經網路對該資料集進行訓練，為了分析正則化對構建神經網路的作用，我們分別構建無正則化模型、L2正則化模型和dropout模型，並對三者的結果進行對比研究。

二、深層神經網路模型

在該文中已經詳細說明過模型所用到的各函式的意義，再此不再贅述。

def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0,keep_prob = 1):

    grads = {}
    costs = []
    m = X.shape[1]
    layers_dims = [X.shape[0], 20, 3, 1]

    parameters = initialize_parameters(layers_dims)

    for i in range(0, num_iterations):

        if keep_prob == 1:
            a3, cache = forward_propagation(X, parameters)

        elif keep_prob < 1:
            a3, cache = forward_propagation_with_dropout(X, parameters)

        if lambd == 0:
            cost = compute_cost(a3, Y)

        else:
            cost = compute_cost_with_regularization(a3, Y, parameters, lambd)

        assert(lambd == 0 or keep_prob == 1)

        if lambd == 0 and keep_prob == 1:
            grads = backward_propagation(X, Y, cache)

        elif lambd != 0:
            grads = backward_propagation_with_regularization(X, Y, cache, lambd)

        elif keep_prob < 1:
            grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)

        parameters = update_parameters(parameters, grads, learning_rate)

        if print_cost == True and i % 10000 ==0:
            print("cost after iterations {}:{}".format(i,cost))
        if print_cost == True and i % 1000 ==0:
            costs.append(cost)

    plt.plot(costs)
    plt.xlabel("iterations (per 1000)")
    plt.ylabel("cost")
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters
 

三、無正則化模型

我們先測試一下模型沒有正則化和dropout優化的情況下，測試效果是怎樣的

parameters = model(train_X, train_Y)
print("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

cost after iterations 0:0.6557412523481002
cost after iterations 10000:0.16329987525724213
cost after iterations 20000:0.13851642423245572
 

On the training set:
Accuracy: 0.9478672985781991
On the test set:
Accuracy: 0.915

在訓練集和測試集上的預測精度分別是94.78%，91.5%，訓練集上精度比測試集高3%，看起來有些過擬合，我們打印出邊界曲線看下效果。

圖中可以明顯看出，對於測試集確實有些過擬合，下面我們使用L2正則化和dropout方法，看看如何改善過擬合現象。

四、L2正則化模型

L2範數在神經網路中也成為F範數（弗羅貝尼烏斯範數），在使用L2正則化的同時，cost函式也需要進行相應的修改。

def compute_cost_with_regularization(A3, Y, parameters, lambd):
    m = Y.shape[1]
    W1 = parameters["W1"]
    W2 = parameters["W2"]
    W3 = parameters["W3"]

    cross_entropy_cost = compute_cost(A3, Y)

    L2_regularization_cost = (1. / m * lambd / 2) * (np.sum(np.square(W1))+
                                                     np.sum(np.square(W2))+
                                                     np.sum(np.square(W3)))
    cost = cross_entropy_cost + L2_regularization_cost

    return cost

def backward_propagation_with_regularization(X, Y, cache, lambd):
    m = X.shape[1]
    (Z1, A1, W1, b1,Z2, A2, W2, b2,Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = 1. / m * np.dot(dZ3, A2.T) + lambd / m * W3
    db3 = 1. / m * np.sum(dZ3, axis=1, keepdims = True)

    dA2 = np.dot(W3.T, dZ3)
    dZ2 = np.multiply(dA2, np.int64(A2>0))
    dW2 = 1. / m * np.dot(dZ2, A1.T) + lambd / m * W2
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims = True)

    dA1 = np.dot(W2.T, dZ2)
    dZ1 = np.multiply(dA1, np.int64(A1>0))
    dW1 = 1. / m * np.dot(dZ1, X.T) + lambd / m * W1
    db1 = 1. / m * np.sum(dZ1, axis=1, keepdims = True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
             "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
             "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

我們設lambd = 0.7，執行模型觀察預測效果：

cost after iterations 0:0.6974484493131264
cost after iterations 10000:0.26849188732822393
cost after iterations 20000:0.2680916337127301

parameters = model(train_X, train_Y, lambd = 0.7)
print("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

On the training set:
Accuracy: 0.9383886255924171
On the test set:
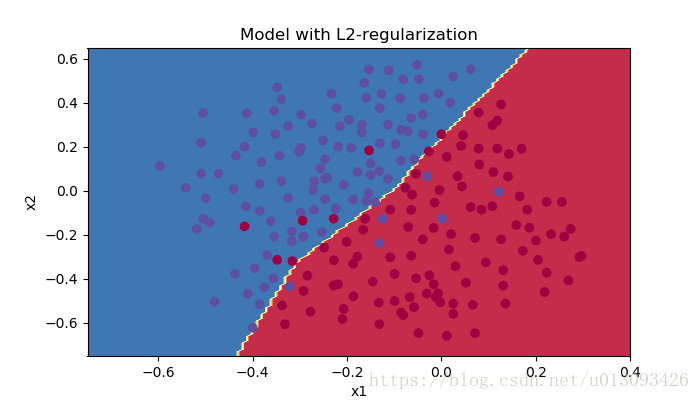
Accuracy: 0.93

此時增加L2正則化後，訓練集和測試集的預測精度分別是93.8%和93%

plt.title("Model with L2-regularization")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x : predict_dec(parameters, x.T),train_X, train_Y)

過擬合現象大大改善。

五、dropout模型

dropout的基本原理在每層網路上隨即的讓一些神經元失活，這樣使得網路模型更加簡化，可以改善過擬合現象。dropout作用的網路層通常是W比較複雜的，對於只有少數神經元的層次則不需要作用。增加dropout演算法後，前向傳播和反向傳播的過程都會受到影響。

（1）前向傳播

def forward_propagation_with_dropout(X, parameters, keep_prob=0.5):
    np.random.seed(1)
    
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    W3 = parameters["W3"]
    b3 = parameters["b3"] 
    
    Z1 = np.dot(W1,X) + b1
    A1 = relu(Z1)
    D1 = np.random.rand(A1.shape[0], A1.shape[1])
    D1 = D1 < keep_prob
    A1 = A1 * D1
    A1 = A1 / keep_prob

    Z2 = np.dot(W2, A1) + b2
    A2 = relu(Z2)
    D2 = np.random.rand(A2.shape[0], A2.shape[1])
    D2 = D2 < keep_prob
    A2 = A2 * D2
    A2 = A2 / keep_prob

    Z3 = np.dot(W3, A2) + b3
    A3 = sigmoid(Z3)

    cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)

    return A3, cache

（2）反向傳播

def backward_propagation_with_dropout(X, Y, cache, keep_prob):
    m = X.shape[1]
    (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cache

    dZ3 = A3 - Y
    dW3 = 1. / m * np.dot(dZ3, A2.T)
    db3 = 1./ m * np.sum(dZ3, axis = 1, keepdims = True)

    dA2 = np.dot(W3.T, dZ3)
    dA2 = dA2 * D2
    dA2 = dA2 / keep_prob
    dZ2 = np.multiply(dA2, np.int64(A2>0))
    dW2 = 1. / m * np.dot(dZ2, A1.T)
    db2 = 1. / m * np.sum(dZ2, axis=1, keepdims = True)

    dA1 = np.dot(W2.T, dZ2)
    dA1 = dA1 * D1
    dA1 = dA1 / keep_prob
    dZ1 = np.multiply(dA1, np.int64(A1>0))
    dW1 = 1. / m * np.dot(dZ1, X.T)
    db1 = 1. / m * np.sum(dZ1, axis = 1, keepdims = True)

    gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,
                 "dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1,
                 "dZ1": dZ1, "dW1": dW1, "db1": db1}

    return gradients

我們給定Keep_prob為0.86，即以24%的概率失活各層神經元，呼叫模型如下

parameters = model(train_X, train_Y, keep_prob = 0.86, )
print("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

cost after iterations 0:0.6543912405149825
cost after iterations 10000:0.0610169865749056
cost after iterations 20000:0.060582435798513114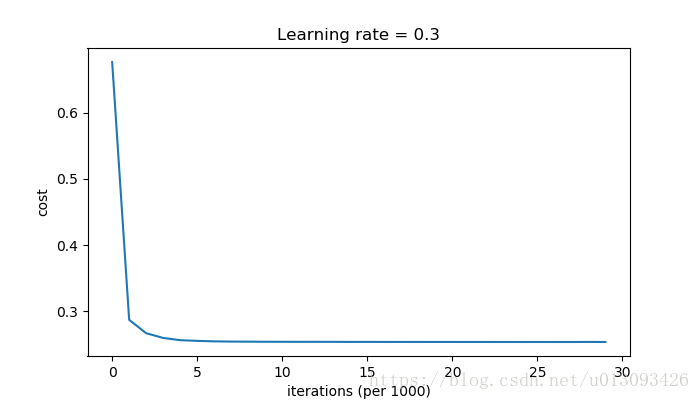

On the train set:
Accuracy: 0.9289099526066351
On the test set:
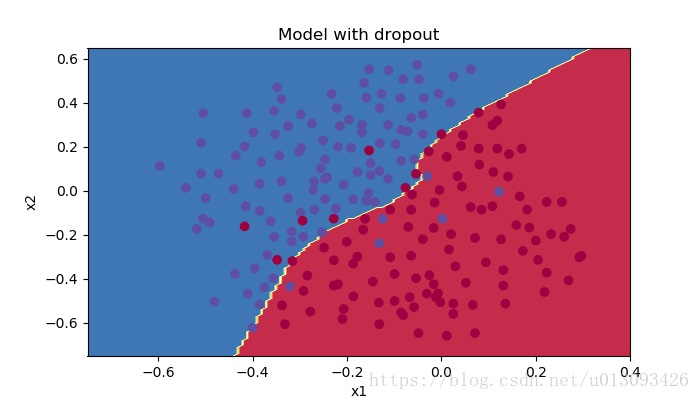
Accuracy: 0.95

該方法在訓練集和測試集上的預測精度分別是92.89%和95，在訓練集上的預測效果更有，過擬合問題得到了很好的解決。

plt.title("Model with dropout")
axes = plt.gca()
axes.set_xlim([-0.75,0.40])
axes.set_ylim([-0.75,0.65])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

六、總結

正則化可以很好的解決模型過擬合的問題，常見的正則化方式有L2正則化和dropout，但是正則化是以犧牲模型的擬合能力來達到平衡的，因此在對訓練集的擬閤中有所損失。