C語言和 C#語言中，對於浮點型的資料採用單精度型別(float)和雙精度型別(double)來儲存：

float 資料佔用 32bit；

double 資料佔用 64bit；

我們在宣告一個變數 float f = 2.25f 的時候，是如何分配記憶體的呢？

其實不論是 float 型別還是 double 型別，在儲存方式上都是遵從IEEE的規範：

float 遵從的是 IEEE R32.24；

double 遵從的是 IEEE R64.53；

單精度或雙精度在儲存中，都分為三個部分：

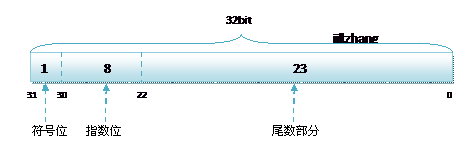
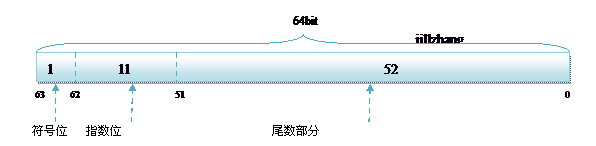
符號位 (Sign)：0代表正數，1代表為負數；

指數位 (Exponent)：用於儲存科學計數法中的指數資料；

尾數部分 (Mantissa)：採用移位儲存尾數部分；

單精度 float 的儲存方式如下：

雙精度 double 的儲存方式如下：

R32.24 和 R64.53 的儲存方式都是用科學計數法來儲存資料的，比如：

8.25  用十進位制表示為：8.25 * 10⁰

120.5 用十進位制表示為：1.205 * 10²

而計算機根本不認識十進位制的資料，他只認識0和1。所以在計算機儲存中，首先要將上面的數更改為二進位制的科學計數法表示：

8.25   用二進位制表示為：1000.01

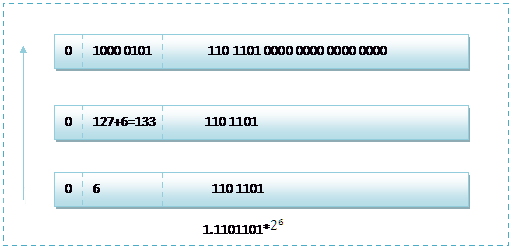
118.5 用二進位制表示為：1110110.1

而用二進位制的科學計數法表示 1000.1，可以表示為1.0001 * 2³

而用二進位制的科學計數法表示 1110110.1，可以表示為1.1101101 * 2⁶

任何一個數的科學計數法表示都為1. xxx * 2ⁿ ，尾數部分就可以表示為xxxx，由於第一位都是1嘛，幹嘛還要表示呀？所以將小數點前面的1省略。

由此，23bit的尾數部分，可以表示的精度卻變成了24bit，道理就是在這裡。（float有效位數相應的也會發生變化,而double則不會，因達不到）

那 24bit 能精確到小數點後幾位呢？我們知道9的二進位制表示為1001，所以 4bit 能精確十進位制中的1位小數點，24bit就能使 float 精確到小數點後6位；

而對於指數部分，因為指數可正可負(佔1位)，所以8位的指數位能表示的指數範圍就只能用7位，範圍是:-127至128。所以指數部分的儲存採用移位儲存，儲存的資料為元資料 +127。

注意：

元資料+127：大概是指“指數”從00000000開始（表示-127）至11111111（表示+128）

所以，10000000表示指數1 (127 + 1 = 128 --> 10000000 ) ；

指數為 3，則為 127 + 3 = 130，表示為 01111111 + 11 = 10000010 ；

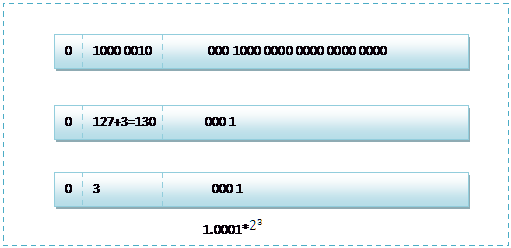
下面就看看 8.25 和 118.5 在記憶體中真正的儲存方式:

8.25 用二進位制表示為：1000.01

8.25 用二進位制的科學計數法表示為: 1.0001* 2³ ，按照上面的儲存方式：

    符號位為：0，表示為正；

    指數位為：3+127=130，即 10000011；

    尾數部分為：0001；

故8.25的儲存方式如下圖所示：

而單精度浮點數118.5的儲存方式如下圖所示：

那麼如果給出記憶體中一段資料，並且告訴你是單精度儲存的話，你將如何知道該資料的十進位制數值呢？

其實就是對上面運算的反推過程，比如給出如下記憶體資料：01000010111011010000000000000000，

首先我們現將該資料分段：0  10000101  11011010000000000000000，在記憶體中的儲存就為下圖所示：

根據我們的計算方式，可以計算出這樣一組資料表示為：

1.1101101*2^(133-127=6) =1.1101101 * 2⁶ = 1110110.1=118.5

而雙精度浮點數的儲存和單精度的儲存大同小異，不同的是指數部分和尾數部分的位數。所以這裡不再詳細的介紹雙精度的儲存方式了，只將118.5的最後儲存方式圖給出：

下面就這個知識點來解決一個疑惑，請看下面一段程式，注意觀察輸出結果：

class 浮點數
    {
        static void Main(string[] args)
        {
            float f = 2.2f;
            double d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));
            //結果："2.2000000476837"

            f = 2.25f;
            d = (double)f;
            Console.WriteLine(d.ToString("0.0000000000000"));
            //結果："2.2500000000000"

            //2.25 - 2.2 = 0.05 ( 但實際結果不是0.05 )
            float f2 = 2.25f - 2.2f;
            Console.WriteLine(f2.ToString("0.0000000000000"));
            //結果："0.0499999500000"
        }
    }

輸出的結果可能讓大家疑惑不解：

單精度的 2.2 轉換為雙精度後，精確到小數點後13位之後變為了2.2000000476837

而單精度的 2.25 轉換為雙精度後，變為了2.2500000000000

為何 2.2 在轉換後的數值更改了，而 2.25 卻沒有更改呢？

其實通過上面關於兩種儲存結果的介紹，我們大概就能找到答案。

2.25 的單精度儲存方式表示為：0 10000001 00100000000000000000000

2.25 的雙精度儲存方式表示為：0 10000000 0010010000000000000000000000000000000000000000000000000

這樣 2.25 在進行強制轉換的時候，數值是不會變的。

而我們再看看 2.2，用科學計數法表示應該為：

將十進位制的小數轉換為二進位制的小數的方法是：將小數*2，取整數部分。

0.2×2=0.4，所以二進位制小數第一位為0.4的整數部分0；

0.4×2=0.8，第二位為0.8的整數部分0；

0.8×2=1.6，第三位為1；

0.6×2=1.2，第四位為1；

0.2×2=0.4，第五位為0；

...... 這樣永遠也不可能乘到=1.0，得到的二進位制是一個無限迴圈的排列 00110011001100110011...

對於單精度資料來說，尾數只能表示 24bit 的精度，所以2.2的 float 儲存為:

但是這種儲存方式，換算成十進位制的值，卻不會是2.2。

因為在十進位制轉換為二進位制的時候可能會不準確（如：2.2），這樣就導致了誤差問題！

並且 double 型別的資料也存在同樣的問題！

所以在浮點數表示中，都可能會不可避免的產生些許誤差！

在單精度轉換為雙精度的時候，也會存在同樣的誤差問題。

而對於有些資料（如2.25），在將十進位制轉換為二進位制表示的時候恰好能夠計算完畢，所以這個誤差就不會存在，也就出現了上面比較奇怪的輸出結果。

      本人對其中的一些細節和錯誤進行了精心的調整。