周志華的西瓜書機器學習被譽為是機器學習的入門寶典，但是這本書對於深度學習的知識介紹非常少，僅僅只是在第五章《神經網路》中對其進行簡單的概括。
這一章對於深度學習的介紹非常淺顯，沒有很深入的對其中的知識進行挖掘，也沒有很複雜的數學推導。
博主在這裡對反向傳播演算法進行數學推導，這裡我使用的方法和周老師有些不同，或許更方便一些。

一、反向傳播演算法概述

誤差反向傳播演算法又稱為BP演算法，是由Werbos等人在1974年提出來的，我們熟知的Hinton也對該演算法做出非常巨大的貢獻。這是一種在神經網路中最為有效的訓練演算法，直到現在還在深度學習中發揮著極其重要的作用。

它是利用輸出後的誤差來估計輸出層前一層的誤差，再用這個誤差估計更前一層的誤差，如此一層一層地反傳下去，從而獲得所有其它各層的誤差估計。這是一種屬於有監督學習的方式，可以對網路中的連線權重做動態調整。

反向傳播演算法和正向傳播演算法相對應，一起構成了神經網路的整個過程：

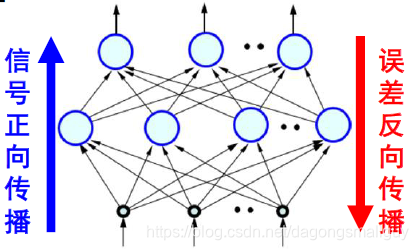
二、數學推導

在這裡，為方便對模型的理解和數學推導，我們沒有采用西瓜書中的模型表示方式，而是用下圖來對其進行簡化：

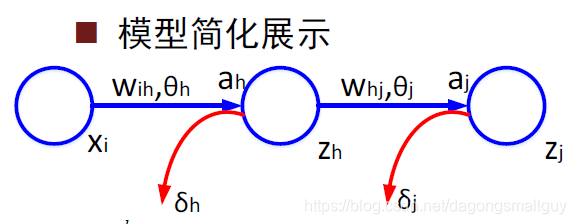
• 與輸入層相關的變數和引數：下標 $i$
• 與隱含層相關的變數和引數：下標 $h$
• 與輸出層相關的變數和引數：下標 $j$
• 激勵函式的輸入： $a$
  a
• 激勵函式的輸出： $z$
• 節點誤差： $\delta$

則輸入隱藏層和輸出層的量分別為：
$a_{h}=\sum_{i=1}^{d}w_{ih}x_{i}+\Theta _{h}$ $a_{j}=\sum_{i=1}^{d}w_{hj}x_{i}+\Theta _{h}$
隱含層和輸出層的的輸出分別是：
$z_{h}=f\left ( a_{h} \right )$ $z_{j}=f\left ( a_{j} \right )$

函式的誤差損失為： $E_{k}=\frac{1}{2}\sum_{j=l}\left ( t_{j}-z_{j} \right )^{2}$
BP演算法是基於梯度下降的策略，以目標的負梯度方向對引數進行調整，所以我們用鏈式法則求出誤差的梯度為：
$\frac{ \partial E}{\partial w_{hj}}=\frac{\partial E}{\partial z_{j}}\frac{\partial z_{j}}{\partial a_{j}}\frac{\partial a_{j}}{\partial w_{hj}}$

由前文我們得到的關係有： $\frac{\partial a_{j}}{\partial w_{hj}}=z_{h}$ $\frac{\partial E}{\partial z_{j}}\frac{\partial z_{j}}{\partial a_{j}}=\frac{\partial E}{\partial a_{j}}=-\left ( t_{j}-z_{j} \right ){f}'\left ( a_{j} \right )$
所以，綜上所得，我們有：
$g(h)=\frac{ \partial E}{\partial w_{hj}}=\frac{\partial E}{\partial z_{j}}\frac{\partial z_{j}}{\partial a_{j}}\frac{\partial a_{j}}{\partial w_{hj}}==-\left ( t_{j}-z_{j} \right ){f}'\left ( a_{j} \right )z_{h}$