影象卷積的理解
本部落格談談對以下兩個問題的理解:
1. 為何影象的卷積是對應元素相乘並求和;
2 為何影象的卷積可以實現影象的模糊或銳化的作用。
問題一:
先借助別人的部落格,說明下影象卷積的操作:
1.1 影象卷積的操作方法:
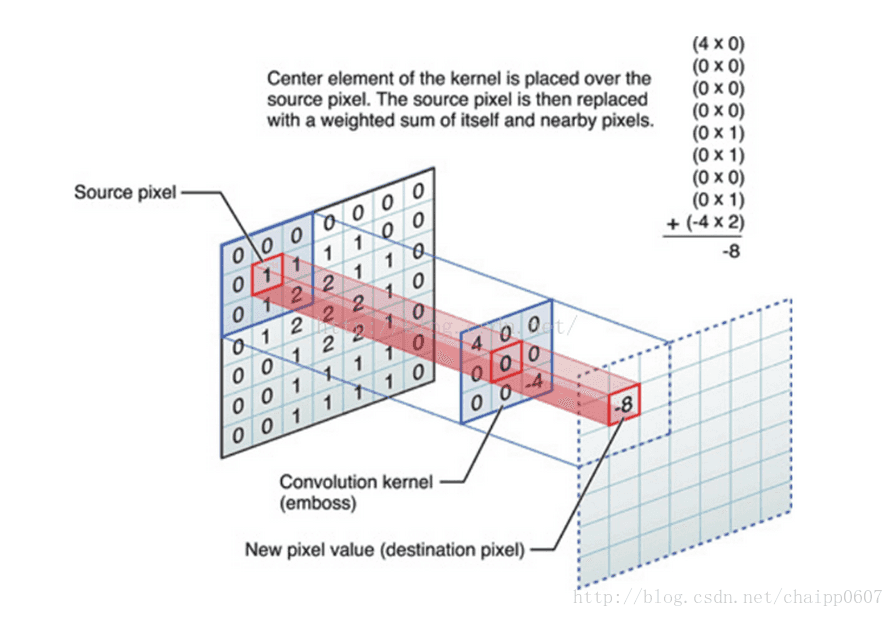
數字影象是一個二維的離散訊號,對數字影象做卷積操作其實就是利用卷積核(卷積模板)在影象上滑動,將影象點上的畫素灰度值與對應的卷積核上的數值相乘,然後將所有相乘後的值相加作為卷積核中間畫素對應的影象上畫素的灰度值,並最終滑動完所有影象的過程。
這張圖可以清晰的表徵出整個卷積過程中一次相乘後相加的結果:該圖片選用3*3的卷積核,卷積核內共有九個數值,所以圖片右上角公式中一共有九行,而每一行都是影象畫素值與卷積核上數值相乘,最終結果-8代替了原影象中對應位置處的1。這樣沿著圖片一步長為1滑動,每一個滑動後都一次相乘再相加的工作,我們就可以得到最終的輸出結果。除此之外,卷積核的選擇有一些規則:
1)卷積核的大小一般是奇數,這樣的話它是按照中間的畫素點中心對稱的,所以卷積核一般都是3x3,5x5或者7x7。有中心了,也有了半徑的稱呼,例如5x5大小的核的半徑就是2。
2)卷積核所有的元素之和一般要等於1,這是為了原始影象的能量(亮度)守恆。其實也有卷積核元素相加不為1的情況,下面就會說到。
3)如果濾波器矩陣所有元素之和大於1,那麼濾波後的影象就會比原影象更亮,反之,如果小於1,那麼得到的影象就會變暗。如果和為0,影象不會變黑,但也會非常暗。
4)對於濾波後的結構,可能會出現負數或者大於255的數值。對這種情況,我們將他們直接截斷到0和255之間即可。對於負數,也可以取絕對值。
1.2 對卷積操作的理解:
首先需要理解卷積公式:
因為影象是二維離散,所以直接理解離散二維卷積:
這就是f()和X()的卷積, 對於離散變數,其實就是個求和的過程; 對於影象來說, X()是原始的影象, 而f()是模板,就是平時說的kernel核;
對這個公式稍微觀察,就很容易理解卷積其實就是求解對應元素的乘積之和。
1.3 下面舉一例項:
一般卷積模板行列為奇數,輸出影象大小與輸入相同。
設卷積模板F、輸入影象X
卷積模板元素下標調整後,為:
比如求點X(2,2)處的卷積,以公式: Y(2,2)=∑∑F(m,n)×X(2-m,2-n), 其中m和n取-1,0,1;
=F(-1,-1)×X(3,3)+F(-1,0)*X(3,2)+F(-1,1)*X(3,1)
+ F(0,-1)×X(2,3)+F(0,0)*X(2,2)+F(0,1)*X(2,1)
+ F(1,-1)×X(1,3)+F(1,0)*X(1,2)+F(1,1)*X(1,1)
細心的你 可能已經發現, 這9個數的對應關係並不是 1.1節 中的對應, 而是相差了180°, 所以影象處理中, 一般情況下 ,現將模板旋轉180°,然後再進行對應位置元素相乘並求和。
二、為何卷積可以有影象的模糊和銳化等效果。
這要從卷積的性質說起:
時域和頻域的卷積關係有:
f(x,y)*g(x,y)=F(u,v)×G(u,v)
其中f()和g()是時域的影象,*表示卷積, 而F和G是對應的傅立葉變化。
時域中的卷積相當於在頻率域中的乘積。 這是個對應關係,可以幫助理解:
比如g1(x,y)是高斯核, 它的頻率域G是個低通濾波器, 則F和G的乘積,結果只有低頻被通過,而高頻被過濾掉, 高頻部分是影象的細節部分, 這樣在時域中與g1的卷積就實現了去除影象細節部分 模糊效果;
再比如g2(x,y)是高斯核, 它的頻率域G是個高通濾波器, 則F和G的乘積,結果只有高頻被通過,而低頻被過濾掉, 低頻部分是輪廓資訊, 這樣在時域中與g2的卷積就實現了銳化效果;
可以設計各種各樣的卷積核函式, 來實現卷積操作, 達到不同的效果。
相關推薦
OpenCV下利用傅立葉變換和逆變換實現影象卷積演算法,並附自己對於卷積核/模板核算子的理解!
學過訊號與系統的人都知道,卷積運算一般是轉化成頻率乘積再求逆來計算,因為這樣可以減少計算量,提高程式碼的效率。 影象卷積操作廣泛應用在影象濾波技術中。 影象卷積運算中一個重要概念是卷積核算子,它是模板核算子的一種,模板核算子實際上就是一個視窗矩陣,用這個視窗按畫素點滑動去
影象卷積的理解
本部落格談談對以下兩個問題的理解: 1. 為何影象的卷積是對應元素相乘並求和; 2 為何影象的卷積可以實現影象的模糊或銳化的作用。 問題一: 先借助別人的部落格,說明下影象卷積的操作: 1.1 影象卷積的
CNN中的卷積理解和實例
垂直 name 平移 圖片 維度 都是 logs 窗口大小 表示 卷積操作是使用一個二維卷積核在在批處理的圖片中進行掃描,具體的操作是在每一張圖片上采用合適的窗口大小在圖片的每一個通道上進行掃描。 權衡因素:在不同的通道和不同的卷積核之間進行權衡 在tensorflow中的
cnn卷積理解
激活 不同 2個 原因 進行 處理 cnn 輸出 輸入 首先輸入圖像是28*28處理好的圖。 第一層卷積:用5*5的卷積核進行卷積,輸入為1通道,輸出為32通道。即第一層的輸入為:28*28圖,第一層有32個不同的濾波器,對同一張圖進行卷積,然後輸出為32張特征圖。需要32
多通道影象卷積基礎知識介紹
轉:https://blog.csdn.net/williamyi96/article/details/77648047 1.對於單通道影象+單卷積核做卷積 Conv layers包含了conv,pooling,relu三種層。以python版本中的VGG16模型中的faster_rcnn_
深度學習影象卷積後的尺寸計算公式
輸入圖片大小 W×W Filter大小 F×F 步長 S padding的畫素數 P 於是我們可以得出: N = (W − F + 2P )/S+1 輸出圖片大小為 N×N 如:輸入影象為5*5*3,Filter為3*3*3,在zero pad 為1,步長 S=1 (可先忽略這條
矩陣卷積理解
在影象處理的過程中,經常會看到矩陣卷積的概念,比如說用一個模板去和一張圖片進行卷積,因此很有必要了解矩陣卷積到了做了什麼,具體又是怎麼計算的。 在matlab中有conv2函式對矩陣進行卷積運算,其中有一個shape引數,取值具體有三種: -full - (d
影象卷積、相關以及在MATLAB中的操作
原文:http://www.cnblogs.com/zjutzz/p/5661543.html 影象卷積、相關以及在MATLAB中的操作 區分卷積和相關 影象處理中常常需要用一個濾波器做空間濾波操作。空間濾波操作有時候也被叫做卷積濾波,或者乾脆叫卷積(離散的卷積,不是微
多通道影象卷積
#1.三通道卷積 ##1.1通過設定不同filter 我們在進行影象處理的時候回遇到有色彩的影象,一般都是RGB,三個通道。 這個時候原始矩陣就變成了三維的,他們分別是原來的兩個維度寬width和高he
【Shader特效8】著色器濾鏡、影象卷積與濾波、數字影象處理
##說在開頭: PhotoShop和特效相機中有許多特效的濾鏡。片元著色器時基於片元為單位執行的,完全可以實現特殊的濾鏡效果。要想實現這些濾鏡效果還需要簡單的瞭解《數字影象處理》中的影象卷積與濾波的一些
一維訊號卷積與影象卷積的區別
基礎概念: 卷積神經網路(CNN):屬於人工神經網路的一種,它的權值共享的網路結構顯著降低了模型的複雜度,減少了權值的數量。卷積神經網路不像傳統的識別演算法一樣,需要對資料進行特徵提取和資料重建,可以直接將圖片作為網路的輸入,自動提取特徵,並且對圖形的變形等具有高度不變形。在語音分析和影象識
影象卷積網路模型彙總
New weights files: NASNet, DenseNet fchollet released this on 16 Jan Assets12 densenet121_weights_tf_dim_ordering_tf_kernels.
卷積神經網路CNN(1)——影象卷積與反捲積(後卷積,轉置卷積)
1.前言 傳統的CNN網路只能給出影象的LABLE,但是在很多情況下需要對識別的物體進行分割實現end to end,然後FCN出現了,給物體分割提供了一個非常重要的解決思路,其核心就是卷積與反捲積,所以這裡就詳細解釋卷積與反捲積。 對於1維的卷積,公式(離散
深度學習---影象卷積與反捲積(最完美的解釋)
動態圖1.前言 傳統的CNN網路只能給出影象的LABLE,但是在很多情況下需要對識別的物體進行分割實現end to end,然後FCN出現了,給物體分割提供了一個非常重要的解決思路,其核心就是卷積與反捲積,所以這裡就詳細解釋卷積與反捲積。 對於1維的卷積,公式(離散
【轉】影象卷積與濾波及高斯模糊(gauss blur)的一些知識點
對非影象邊界的畫素的操作比較簡單。假設我們對I的第四個畫素3做區域性平均。也就是我們用2,3和7做平均,來取代這個位置的畫素值。也就是,平均會產生一副新的影象J,這個影象在相同位置J (4) = (I(3)+I(4)+I(5))/3 = (2+3+7)/3 = 4。同樣,我們可以得到J(3) = (I(2)+
Deep Learning 30: 卷積理解
1. 這篇文章以賈清揚的ppt說明了卷積的實質,更說明了卷積輸出影象大小應該為: 假設輸入影象尺寸為W,卷積核尺寸為F,步幅(stride)為S(卷積核移動的步幅),Padding使用P(用於填充輸入影象的邊界,一般填充0),那麼經過該卷積層後輸出的影象尺寸為(W-F+2P)/S+1。 2.它寫出為什麼會用
深度學習-卷積理解
1.這篇文章以賈清揚的ppt說明了卷積的實質,更說明了卷積輸出影象大小應該為: 假設輸入影象尺寸為W,卷積核尺寸為F,步幅(stride)為S(卷積核移動的步幅),Padding使用P(用於填充輸入影象的邊界,一般填充0),那麼經過該卷積層後輸出的影
影象卷積操作的手動實現(基於opencv的C++編譯環境)
opencv環境下有自帶的filter2D()函式可以實現影象的卷積,自己寫一個卷積函式函式貌似是沒事找事。。。。好吧,事實是這是我們計算機視覺課程上的一項作業。我們很多演算法過程僅僅只呼叫別人寫好的介面,即使原理我們已經清楚,但是真正編寫程式碼的時候很多細節
關於影象卷積與caffe中卷積實現
影象卷積及Caffe中的卷積實現 原創內容,轉載請註明出處。 本文簡單介紹了影象卷積相關的知識以及Caffe中的卷積實現方法,寫作過程中參考了很多很讚的資料,有興趣的讀者可以從【參考資料】檢視。 博文中的錯誤和不足之處還望各位讀者指正。 什麼是卷積?
cuda影象卷積
#include <wb.h> #define wbCheck(stmt) do { \ cudaError_t err = st