資料結構——樹——知識點總結
資料結構——樹
定義:樹是一個n(n>=0)個結點的有序合集
名詞理解:
結點:指樹中的一個元素;
結點的度:指結點擁有的子樹的個數,二叉樹的度不大於2;
數的度:指樹中的最大結點度數;
葉子:度為0的結點,也稱為終端結點;
高度:葉子節點的高度為1,根節點高度最高;
層:根在第一層,以此類推;
二叉樹的定義:由一個結點和兩顆互不相交、分別稱為這個根的左子樹和右子樹的二叉樹構成(遞迴定義)
二叉樹的性質:
1:二叉樹的第i層上至多有2^(i-1)個結點
2:深度為k的二叉樹,至多有2^k-1個結點
滿二叉樹:葉子節點一定要在最後一層,並且所有非葉子節點都存在左孩子和右孩子;
最特別的二叉樹:完全二叉樹
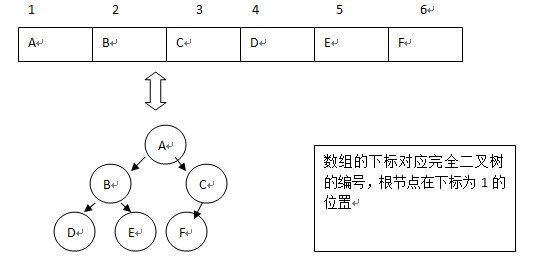
完全二叉樹的性質:
1:結點 i 的子結點為2*i 和 2*i+1(前提是都小於總結點數)
2:結點 i 的父結點為 i/2
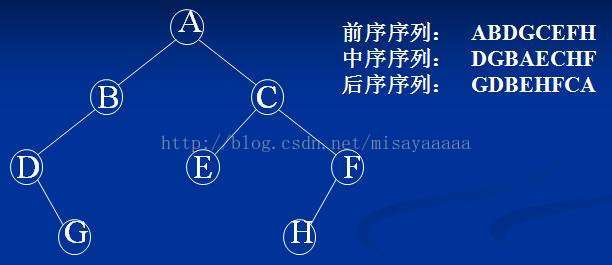
二叉樹的遍歷(要有遞迴的思想!!!):
1:先序遍歷:根->左子樹->右子樹(先序)
2:中序遍歷:左子樹->根->右子樹(中序)
3:後序遍歷:左子樹->右子樹->根(後序)
這三種遍歷方法只是訪問結點的時機不同,訪問結點的路徑都是一樣的,時間和空間複雜度皆為O(n)
二叉樹的儲存結構:
2:鏈式儲存(最普遍的儲存方式)——由於結點可能為空,所以會比較浪費空間
如果有n個節點,則有2n個left、right指標,但是用到的只有n-1個指標
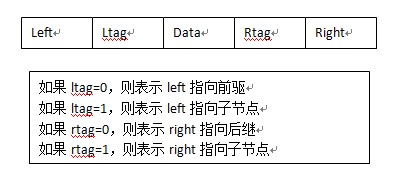
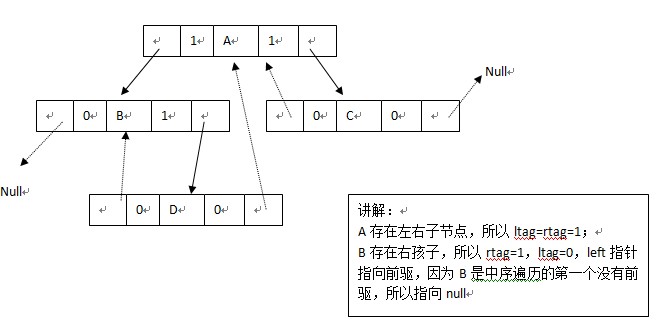
3:線索儲存(改進的方法)
關於霍夫曼編碼(Huffman編碼):
Huffman是一種字首編碼;Huffman編碼是建立在Huffman樹的基礎上進行的,因此為了進行Huffman編碼,必須先構建Huffman樹;樹的路徑長度是每個葉節點到根節點的路徑之和;帶權路徑長度是(每個葉節點的路徑長度*wi)之和;Huffman樹是最小帶權路徑長度的二叉樹;
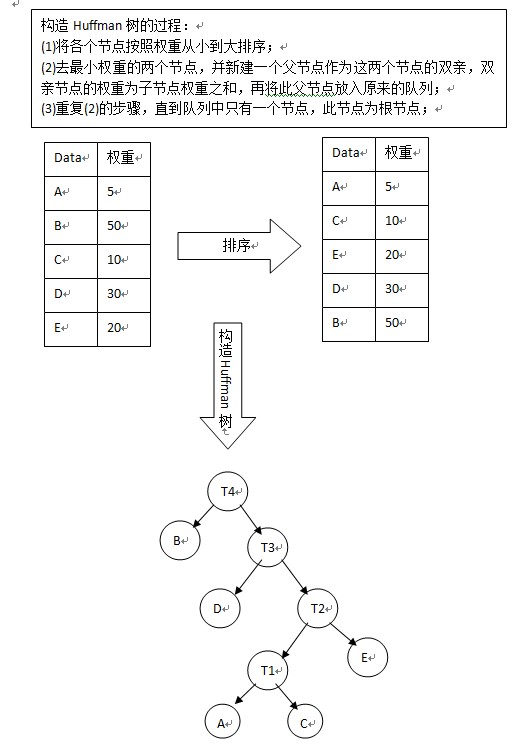
構造Huffman樹的過程:
(1)將各個節點按照權重從小到大排序;
(2)取最小權重的兩個節點,並新建一個父節點作為這兩個節點的雙親,雙親節點的權重為子節點權重之和,再將此父節點放入原來的佇列;
(3)重複(2)的步驟,直到佇列中只有一個節點,此節點為根節點;
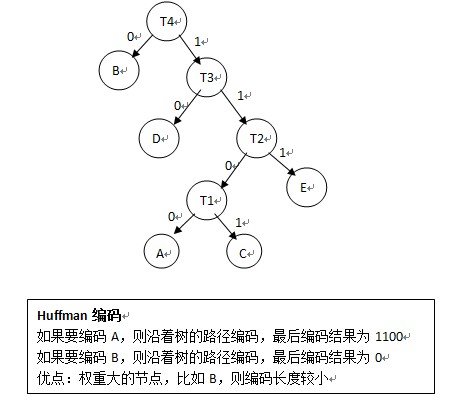
構造完Huffman樹之後,就可以進行Huffman編碼了,編碼規則:左分支填0,右分支填1;
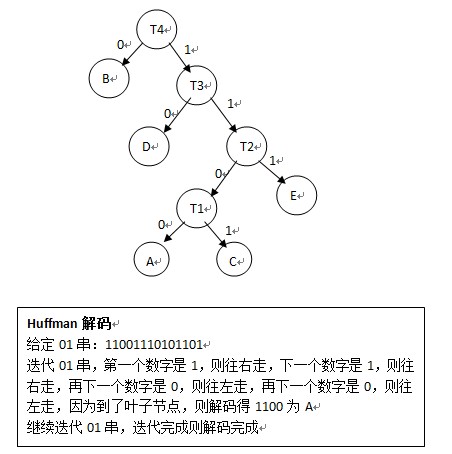
Huffman解碼過程:給定一個01串,將01串進行Huffman樹,到葉子節點了就表明已經解碼一個節點,然後再次遍歷Huffman樹;
相關推薦
資料結構——樹——知識點總結
資料結構——樹 定義:樹是一個n(n>=0)個結點的有序合集 名詞理解: 結點:指樹中的一個元素; 結點的度:指結點擁有的子樹的個數,二叉樹的度不大於2; 數的度:指樹中的最大結點度數; 葉子
資料結構-圖-知識點總結
一、基本術語 圖(graph):圖是由頂點的有窮非空集合和頂點之間邊的集合組成,通常表示為:G(V,E),其中,G表示一個圖,V是圖G中的頂點的集合,E是圖G中邊的集合。 頂點(Vertex):圖中的資料元素。線性表中我們把資料元素叫元素,樹中將資料元素叫結點。 邊:頂點之間的邏輯關係用邊來表示,邊集可
資料結構---圖---知識點總結
轉自:https://blog.csdn.net/Ontheroad_/article/details/72739380圖的儲存結構1.鄰接矩陣:兩個陣列,一個數組儲存“頂點集”,一個數組儲存“邊集”。無向圖中:有向圖中:2.鄰接表:陣列與連結串列相結合的儲存方法。對於帶權值
數據結構二叉樹知識點總結
高度 總結 每一個 數據結構 後序 bsp 總數 結構 如果 術語 1. 節點的度:一個節點含有的子樹的個數稱為該節點的度; 2. 葉節點或終端節點:度為零的節點; 3. 非終端節點或分支節點:度不為零的節點; 4. 父親節點或父節點:若一個節點含有子節點,則
資料結構與演算法總結——二叉查詢樹及其相關操作
我實現瞭如下操作 插入,查詢,刪除,最大值 樹的高度,子樹大小 二叉樹的範圍和,範圍搜尋 樹的前序,中序,後序三種遍歷 rank 前驅值 在這一版本的程式碼中,我使用了類模板將介面與實現分
(2016秋資料結構課後練習題總結)03-樹2 List Leaves (25分)
Given a tree, you are supposed to list all the leaves in the order of top down, and left to right. Input Specification: Each input file contains one test
(2016秋資料結構課後練習題總結)03-樹1 樹的同構 (25分)
給定兩棵樹T1和T2。如果T1可以通過若干次左右孩子互換就變成T2,則我們稱兩棵樹是“同構”的。例如圖1給出的兩棵樹就是同構的,因為我們把其中一棵樹的結點A、B、G的左右孩子互換後,就得到另外一棵樹。而圖2就不是同構的。 圖1 圖2 現給定兩棵樹,請你判斷它們是否是
數據結構基本知識點總結
ttr 連通 稀疏圖 邏輯結構 時也 實現 alt 相關 散列 1, 數據結構三要素: 1,邏輯結構:線性和非線性 2,存儲結構:順序,鏈式,索引,散列 3,數據運算:算法 具體時間復雜度與問題的規模和初始條件相關,分最佳和最大 2, 線性表: 無頭結點: 頭插
《java常用演算法手冊》 第二章 資料結構 樹 圖
前面我們介紹陣列的資料結構,我們知道對於有序陣列,查詢很快,並介紹可以通過二分法查詢,但是想要在有序陣列中插入一個數據項,就必須先找到插入資料項的位置,然後將所有插入位置後面的資料項全部向後移動一位,來給新資料騰出空間,平均來講要移動N/2次,這是很費時的。同理,刪除資料也是。 然後
資料結構 樹筆記-6 二叉樹的非遞迴先序遍歷
如下這棵二叉樹的先序遍歷結果為:ABDEFPC 針對於上面的這棵二叉樹,結合程式碼,講述遍歷過程: #include <stdio.h>#include <malloc.h> //#define ElemType
資料結構 樹筆記-5 線索二叉樹 以及 線索二叉連結串列
線索二叉連結串列 線索二叉連結串列 來自於 二叉連結串列。一個二叉連結串列,如果存放n個結點,就一定有n+1個空指標域,而線上索鏈 表中,就讓這n+1個空指標域有了用武之地。 空指標域 用於存放 某種遍歷順序下的 前驅或者後繼的地址。 已知 一棵二叉樹的結構:
資料結構 樹筆記-4 二叉樹儲存結構
既然上面提到了二叉樹的儲存結構,那麼我們進一步詳細介紹二叉樹的儲存結構 先複習一下 邏輯結構 與 物理結構: 邏輯結構講究的是資料之間的邏輯關係,分為:集合結構、線性結構、樹形結構、圖形結構 物理結構講究的是資料的儲存結構,分為:順序儲存結構、鏈式儲存結構
嚴蔚敏-資料結構-樹的遍歷
前序非遞迴遍歷 PreOrderTraverse(BiTree T) { InitStack(S); p=T; while (p||!StackEmpty) { if(p) { print(p); if(p->rchild) {
資料結構 樹筆記-9 直接插入排序
內排序:待排序列完全放在記憶體中,適用於待排序列中的元素個數不多,足以在記憶體中進行。 外排序:排序過程除了需要在記憶體中進行,還需要訪問外儲存器,因為待排序列中的元素個數個數太多了。 內排序 之 插入排序 插入排序 之 直接插入排序
資料結構 樹筆記-8 哈夫曼樹的構建與儲存
講述哈夫曼樹的構建過程(按照程式碼的思路): 程式碼: #include <stdio.h> #include <malloc.h> typedef struct{ int weight; int parent
資料結構 樹筆記-7 二叉樹的非遞迴中序遍歷
二叉樹的 非遞迴 中序遍歷 //#define ElemType char typedef char ElemType; 結點中存放的資料的型別的定義
【極客時間】資料結構與演算法總結
【極客時間】資料結構與演算法總結: 02| 資料結構是為演算法服務的,演算法要作用在特定的資料結構之上。 20個最常用的最基礎的資料結構與演算法: 10個數據結構:陣列、連結串列、棧、佇列、散列表、二叉樹、堆、跳錶、圖、Trie樹 10個演算法:遞迴、排序、二分
資料結構————樹狀陣列
原陣列--->字首和------>範圍和 原陣列更改陣列元素在求和效率較低,引入樹狀陣列 假設原陣列A【】 樹狀陣列C【】 樹狀陣列 的三種操作: 1.lowbit() 子葉數(二進位制最低位的1代表多少) 程式碼實現: int lo
leetcode與資料結構---動態規劃總結(一)
這幾天一直在做leetcode上關於動態規劃方面的題目,雖然大二下的演算法設計課上較為詳細的講過動態規劃,奈何遇到新穎的題目或者稍加背景的題目立刻就原形畢露不知題目所云了。動態規劃算是較難的一個專題了,但只要找到遞推關係其最終的程式碼又相當簡便。現在把這幾天做過的題目整理總結一下,畢竟只求做
資料結構-樹狀陣列(二)
複習筆記-樹狀陣列(二) 樹狀陣列(一) 略微進階的操作 在樹狀陣列(一)中,身為打線段樹要耗費好長時間(其實都不一定能揹著打出來)的蒟蒻,我安利了一波樹狀陣列,並且介紹了區間查詢和單點修改的基本操作。那麼,對基礎的樹狀陣列進行一些修改,結合差分,就可以同時進行區間修改和單點查詢。 差分陣列 儲存方