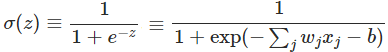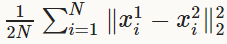Deep Learning 基礎 -- 啟用函式/損失函式
Deep Learning 基礎 – 啟用函式/損失函式
Tags: Deep_Learning
本文主要包含如下內容:
啟用函式
如果不使用啟用函式,你的網路的分類能力基本等同於一個線性分類器(線性迴歸),網路表達能力不足,無法逼近任意函式,所以啟用函式是相當關鍵的。
啟用函式的特徵:非線性\可微性(用於梯度下降演算法)\單調性(保證單層網路是凸函式)
Sigmoid非線性函式
優點:
它輸入實數值並將其壓縮到0到1範圍內,即很大的負數變為0,很大的正數變為1。
缺點:
Sigmoid函式飽和使梯度消失:當函式啟用值接近於0或者1時,函式的梯度接近於0。在反向傳播計算梯度過程中:每層殘差接近於0,計算出的梯度也不可避免地接近於0。這樣在引數微調過程中,會引起引數彌散問題,傳到前幾層的梯度已經非常靠近0了,引數幾乎不會再更新。為了防止梯度消失,必須對於權重矩陣初始化
Sigmoid函式的輸出不是零中心的。這會導致後一層的神經元將得到上一層輸出的非 0 均值的訊號作為輸入。
exp指數函式運算複雜,會花費大量的時間。
Tanh非線性函式
導數為:f(z)’ = 1 − (f(z))2,最大值為1.
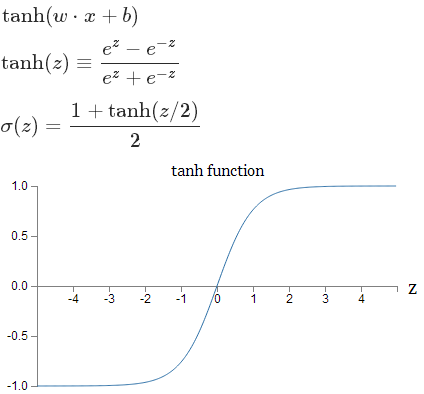

它將實數值壓縮到[-1,1]之間。和
sigmoid神經元一樣,它也存在飽和問題,但是和sigmoid神經元不同的是,它的輸出是零中心的。因此,在實際操作中,tanh非線性函式比sigmoid非線性函式更受歡迎。
ReLU啟用函式

優點:
計算高效:相較於sigmoid和tanh函式,ReLU對於隨機梯度下降的收斂有巨大的加速作用。在反向傳播過程中,減輕了梯度彌散的問題,神經網路前幾層的引數也可以很快的更。
正向傳播過程中,sigmoid和tanh函式計算啟用值時需要計算指數,而Relu函式僅需要設定閾值。如果,如果。加快了正向傳播的計算速度。
ReLU會使一部分神經元的輸出為0,這樣就造成了網路的稀疏性,並且減少了引數的相互依存關係,緩解了過擬合問題的發生。
缺點:
梯度為0或者為1,隨著訓練的推進,部分輸入會落入硬飽和區,導致對應權重無法更新。這種現象被稱為“神經元死亡”。
與sigmoid類似,ReLU的輸出均值也大於0,偏移現象和 神經元死亡會共同影響網路的收斂性。
Leaky ReLU啟用函式
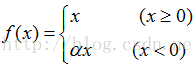
α 是一個很小的常數(如0.25)。這樣,即修正了資料分佈,又保留了一些負軸的值,使得負軸資訊不會全部丟失。
優點:
不會飽和\計算高效\收斂速度快\不會死
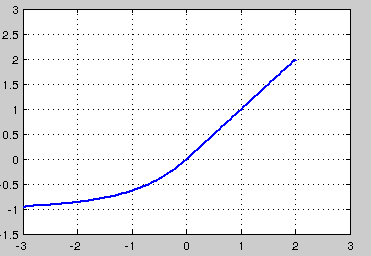
Exponential Linear Units (ELU)
優點:
不會死\輸出接近0均值
缺點:
計算量大,需要指數運算
Maxout啟用函式
Maxout是對ReLU和leaky ReLU的一般化歸納。ReLU和Leaky ReLU都是這個公式的特殊情況(比如ReLU就是當w_1,b_1=0的時候)。這樣Maxout神經元就擁有ReLU單元的所有優點(線性操作和不飽和),而沒有它的缺點(死亡的ReLU單元)。然而和ReLU對比,它每個神經元的引數數量增加了一倍,這就導致整體引數的數量激增。
損失函式
MSE損失 + Sigmoid啟用函式
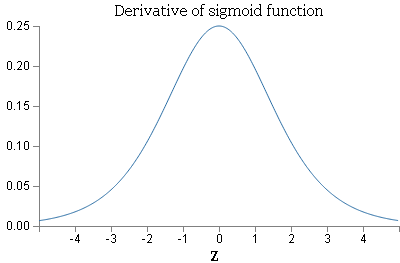
對於Sigmoid,當z的取值越來越大後,函式曲線變得越來越平緩,意味著此時的導數σ′(z)也越來越小。同樣的,當z的取值越來越小時,也有這個問題。僅僅在z取值為0附近時,導數σ′(z)的取值較大。在均方差+Sigmoid的反向傳播演算法中,每一層向前遞推都要乘以σ′(z),得到梯度變化值。Sigmoid的這個曲線意味著在大多數時候,我們的梯度變化值很小,導致我們的W,b更新到極值的速度較慢,也就是我們的演算法收斂速度較慢。

SigmoidCrossEntropyLoss(交叉熵損失+Sigmoid啟用函式)


使用交叉熵,得到的的梯度表示式沒有了σ′(z),梯度為預測值和真實值的差距,這樣求得的Wl,bl的梯度也不包含σ′(z),因此避免了反向傳播收斂速度慢的問題。
SoftmaxWithLoss(廣義線性迴歸分析損失層) (對數似然損失+softmax進行分類輸出)
解決分類問題,輸出層神經元輸出的值在0到1之間,同時所有輸出值之和為1.



可見,梯度計算也很簡潔,也沒有第一節說的訓練速度慢的問題。
EuclideanLoss(歐式損失層)
當預測值與目標值相差很大時, 梯度容易爆炸, 因為梯度裡包含了x−t.
Smooth L1 Loss
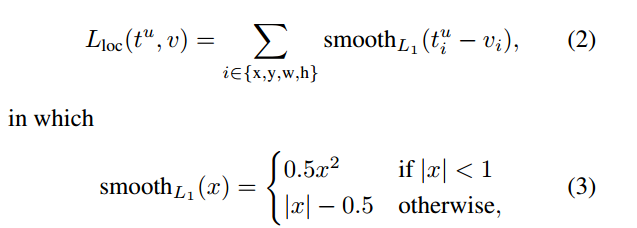
當差值太大時, 原先L2梯度裡的x−t被替換成了±1, 這樣就避免了梯度爆炸, 也就是它更加健壯.
相關推薦
Deep Learning 基礎 -- 啟用函式/損失函式
Deep Learning 基礎 – 啟用函式/損失函式 Tags: Deep_Learning 本文主要包含如下內容: 啟用函式 如果不使用啟用函式,你的網路的分類能力基本等同於一個線性分類器(線性迴歸),網路表達能力不足,無
啟用函式 損失函式 優化器
均方差損失函式+Sigmoid的反向傳播演算法中,每一層向前遞推都要乘以σ′(z)(啟用函式的導數),得到梯度變化值。Sigmoid的這個曲線意味著在大多數時候,我們的梯度變化值很小,導致我們的W,b更新到極值的速度較慢,也就是我們的演算法收斂速度較慢。 使用交叉熵損失函式,得到的梯度表示式沒有
Deep Learning基礎--線性解碼器、卷積、池化
sparse pca 過程 條件 連接 移動 .cn 計算過程 htm 本文主要是學習下Linear Decoder已經在大圖片中經常采用的技術convolution和pooling,分別參考網頁http://deeplearning.stanford.edu/wiki/i
Deep Learning 基礎
原創: 施天璐 Refinitiv創新實驗室ARGO 本文含有部分易懂的數學公式,預計閱讀時間10分鐘 本文是深度學習的基礎入門篇,著重描述以下三個部分: 什麼是深度學習 人工神經網路的概念 反向傳播演算法的理解 &nb
Deep Learning基礎知識點彙總
引言 本篇文章作為筆記形式,記錄一些基礎知識點和好的博文! CNN(卷積神經網路) Dilated/Atrous Convolutions(擴張卷積/空洞卷積) Receptive Field(感受野)
深度學習基礎--loss與啟用函式--合頁損失函式、摺頁損失函式;Hinge Loss;Multiclass SVM Loss
合頁損失函式、摺頁損失函式;Hinge Loss;Multiclass SVM Loss Hinge Loss是一種目標函式(或者說損失函式)的名稱,有的時候又叫做max-margin objective。用於分類模型以尋找距離每個樣本的距離最大的決策邊界,即最大化樣本和邊界之間的邊
深度學習基礎--loss與啟用函式--sigmiod與softmax;對數損失函式與交叉熵代價函式
sigmiod與softmax sigmiod就是邏輯迴歸(解決二分類問題);softmax是多分類問題的邏輯迴歸 雖然邏輯迴歸能夠用於分類,不過其本質還是線性迴歸。它僅線上性迴歸的基礎上,在特徵到結果的對映中加入了一層sigmoid函式(非線性)對映,即先把特徵線性求和,然後使
AI應用開發基礎傻瓜書系列3-啟用函式和損失函式
第三篇:啟用函式和損失函式 在這一章,我們將簡要介紹一下啟用函式和損失函式~ 啟用函式 看神經網路中的一個神經元,為了簡化,假設該神經元接受三個輸入,分別為\(x_1, x_2, x_3\),那麼\(z=\sum\limits_{i}w_ix_i+b_i\), 啟用函式也就是\(A=\sigma(Z)\)
1.3.2【Deep Learning翻譯系列】Activation Functions 啟用函式
1、Sigmoid與雙曲正切 當建立神經網路,要做出的選擇之一是在隱藏層、輸出單元使用什麼啟用函式。 常見如的Sigmoid函式: σ
Deep learning系列(七)啟用函式
1. sigmoid啟用函式 sigmoid將一個實數輸入對映到[0,1]範圍內,如下圖(左)所示。使用sigmoid作為啟用函式存在以下幾個問題: 梯度飽和。當函式啟用值接近於0或者1時,函式的梯度接近於0。在反向傳播計算梯度過程中:δ(l)=(W(l))Tδ(l+1
AI應用開發基礎傻瓜書系列3-損失函式
全套教程請點選:微軟 AI 開發教程 第三篇:啟用函式和損失函式(二) 在這一章,我們將簡要介紹一下損失函式~ 損失函式 作用 在有監督的學習中,需要衡量神經網路輸出和所預期的輸出之間的差異大小。這種誤差函式需要能夠反映出當前網路輸出和實際結果之間一種量化之後的不一致程度,也就是說函式值越大,反映出
1.2.11 【Deep Learning翻譯系列】Explanation of Logistic Regression Cost Function 對數機率迴歸代價函式的說明
視訊地址 本視訊給出在對數機率迴歸使用這個成本函式的理由。 在之前的對數機率迴歸中,預測 y ^
機器學習基礎(四十二)—— 常用損失函式的設計(multiclass SVM loss & hinge loss)
損失函式,又叫代價函式(成本函式,cost function),是應用優化演算法解決問題的關鍵。 1. 0-1 損失函式 誤分類的概率為: P(Y≠f(X))=1−P(Y=f(X)) 我們不妨記 m≜fθ(x)⋅y(其中 y∈{−1,1}。對於二分類
深度神經網路之損失函式和啟用函式
1.損失函式和啟用函式簡介 通過前面深度神經網路之前向傳播演算法和深度神經網路之反向傳播演算法的學習,我們能夠了解到損失函式是用來評估模型的預測值與真實值之間的差異程度。另外損失函式也是神經網路中優化的目標函式,神經網路訓練或者優化的過程就是最小化損失函式的過程
Deep Learning 36:python中的一些函式
snrs, mods = map(lambda j: sorted(list(set(map(lambda x: x[j], Xd.keys())))), [1,0]) 上面這句話的意思是: Xd.keys()取出Xd中的鍵keys,形為('8PSK',-10),故snrs值為:sorted(list(set
Deep Learning 32: 自己寫的keras的一個callbacks函式,解決keras中不能在每個epoch實時顯示學習速率learning rate的問題
1 from __future__ import absolute_import 2 from . import backend as K 3 from .utils.generic_utils import get_from_module 4 from six.moves import z
度量學習(metric learning)損失函式
學習的物件通常是樣本特徵向量的距離,度量學習的目的是通過訓練和學習,減小或限制同類樣本之間的距離,同時增大不同類別樣本之間的距離。常用度量學習損失方法(1)對比損失用於訓練Siamese(孿生)網路,,輸入為兩張圖片,每一對訓練圖片都有一個標籤y,y=1表示兩張圖片屬於同一個
深度學習Deep Learning(04):權重初始化問題2_ReLu激勵函式
三、權重初始化問題2_ReLu激勵函式 1、說明 2、ReLu/PReLu激勵函式 目前ReLu啟用函式使用比較多,而上面一篇論文沒有討論,如果還是使用同樣初始化權重的方法(
《Deep Learning》譯文 第六章 深度前饋網路 從異或函式說起
6.1 從異或函式說起 為了使前饋網路的概念更具體化,我們先從一個簡單地例子說起,這個例子中,我們使用前饋網路解決一個簡單的任務:學習異或函式。 眾所周知,異或(XOR)操作是一種針對二進位制值的二目操作符。當兩個運算元不同
深度學習筆記(三):啟用函式和損失函式
這一部分來探討下啟用函式和損失函式。在之前的logistic和神經網路中,啟用函式是sigmoid, 損失函式是平方函式。但是這並不是固定的。事實上,這兩部分都有很多其他不錯的選項,下面來一一討論 3. 啟用函式和損失函式 3.1 啟