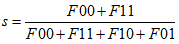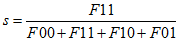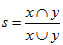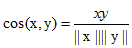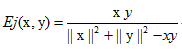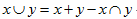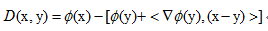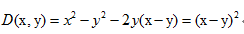Tanimoto相似度與Bregman距離
之前寫過一篇距離與相似性度量的blog,這裡新增兩個少見的相似性度量方法,並且再擴充套件一些東西。
Tanimoto 係數
Tanimoto係數由Jaccard係數擴充套件而來。首先引入Jaccard係數。
Jaccard係數
兩個特徵向量A,B,如果其值都是0,1的二值資料,那麼有一個簡單的判定相似性的方法:
F00 = A中為0並且B中也為0的個數
F10 = A1 B0的個數
F01 = A0 B1的個數
F11 = A1 B1 的個數
那麼可以定義這麼一個similarity:
這叫做(simplematch coefficient)SMC,簡單匹配係數。
很多情況下,兩個向量中,0的個數會大大多於1的個數,也就很稀疏,類不平衡。這時候不同向量之間的SMC會因為過多出現的0而沒有效果。
那麼我們可以只考慮F11,得到:
這也就是Jaccard距離。
如果把兩個向量看作兩個集合,0為此元素不存在,1為此元素存在,那麼Jaccard距離就是很好地比較兩個集合相似性的度量方法。在集合的相似度計算中,Jaccard距離可以寫成:
擴張Jaccard
如果這個時候,還是很稀疏,但是值是非二值的,該怎麼辦?
一種簡單的方法就是用cosine距離:
cosine距離是處理稀疏非二值特徵的很好的選擇。
但是,我們還想以Jaccard距離的思維來做又要如何?如下:
如果我們的x,y都是二值向量,那麼如上公式就會得到Jaccard距離。
分子項,只有兩個均非0才會有非0的有用結果,類似於F11,不過這裡不是簡單的計數,而是用數乘來表示。
分母項,2範數表示大小,也只有非0的項才有貢獻,再減去xy即共同的,這個類似
以上是通過觀察得出的結論,具體推導不知。
SMC距離在一般的非不平衡二值問題上計算應該比較方便。
Jaccard在文字分類等不平衡二值問題上有所作為
Tanimoto的話,沒用過,效果不知道有沒有cosine好。應該會得到一個類似cosine的結果。
Bregman 散度距離
(BregmanDivergence)
形式如下:
其中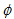
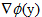
我們把y=x^2作為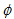
即得到歐式距離。
Bregman距離的數學性質及推導不知,wiki上說,其為許多常見距離的一個通式。
其中包括歐式距離,曼哈頓距離,KL距離等等。水平有限,只能引用到此。
mahalanobis距離
馬氏距離:
首先考慮歐式距離,歐式距離有兩點明顯的缺點:
1.把不同量綱級別的屬性同等看待
比如一個特徵向量包含人的年齡,收入,那麼收入得到的點乘會遠遠大於年齡,使得年齡沒有作用。
一般的做法是歸一化屬性值。
2.屬性間相關性
一個人的體重很多時候正比於身高。如果作為特徵中的兩個屬性,就會重複計算這個值,得到冗餘資訊。
一種做法是做去相關,降維,特徵選擇等等。
不同與歐式距離,馬氏距離考慮了量綱即屬性間相關性。如下:
M(x,y)=(x-y)sigm(x-y)T
其中sigm表示整體特徵向量的協方差矩陣。
馬氏距離的最大缺點就是計算複雜度要高出很多,具體運用時要考慮這個因素。
補充
補充之前距離沒寫到的一些資訊:
轉換 transformation
有時候,我們得到了距離,進而可以用這個距離求相似性。如:
s表示相關性,d表示距離,則有:
s = -d
s=1/(1+d) 這種方法把距離對映到(0-1)的相似性空間中
s=e^-d 這種方法為非線性對映
s = 1-(d-mind)/(maxd-mind) 也是一種把距離對映到(0-1)上的方法,不過這種是線性的。
小結:任意一種遞減的函式都可以把d對映為s度量
歸一化normalization
像cosine這種,本身就是(-1,1)的資料,可以直接使用。不過很多情況下,如歐式距離,range都無從控制。歸一化是必須的。
度量(metric)
滿足以下幾種性質的量,可以成為度量(metric):
非負性
(a)d(x,y)>=0
(b)d(x,y)=0 if x==y
對稱性
d(x,y) = d(y,x) for all x,y
三角性
d(x,z)<= d(x,y) + d(y,z)
metrics對於許多演算法是必須的,不過很多情況下,不必滿足metrics也可以作為距離度量。
有再看到類似的再更新。
相關推薦
Tanimoto相似度與Bregman距離
之前寫過一篇距離與相似性度量的blog,這裡新增兩個少見的相似性度量方法,並且再擴充套件一些東西。 Tanimoto 係數 Tanimoto係數由Jaccard係數擴充套件而來。首先引入Jaccard係數。 Jaccard係數 兩個特徵向量A,B,如果其值都是0,1的
餘弦相似度 與 歐式距離 選擇
轉載自:http://www.cnblogs.com/chaosimple/archive/2013/06/28/3160839.html 餘弦相似度公式: 歐式距離公式: 二維空間的公式 (2)三維空間兩點a(x1,y1,z1)與b(x2,y2,z2)間的歐氏距
餘弦相似度與正規化的歐氏距離的某種等價性
給一個集合, V={x|x∈Rn}V={x|x∈Rn}, 和一個點 u∈Rnu∈Rn, 依次計算uu與VV中各個點的距離, 然後按照從近到遠排序, 就可以得到一個序列A=<x1,x2,...>A=<x1,x2,...>. 距離函式可以取
計算句子文字相似度-編輯距離計算
本文轉載於:https://juejin.im/post/5b237b45f265da59a90c11d6 編輯距離,英文叫做 Edit Distance,又稱 Levenshtein 距離,是指兩個字串之間,由一個轉成另一個所需的最少編輯操作次數,如果它們的距離越大,說明它們越是不同。
白話總結《餘弦相似度vs歐式距離&缺陷》
之前相似度計算很模糊,趁著休息總結一下,以便使用時更針對業務需要。 餘弦相似度 公式中p和q是兩個向量。 餘弦相似度需要對兩個向量的長度做歸一化,然後度量兩個向量的方向,與向量的長度無關。也就是說,兩個向量只要方向一致,無論長度、程度如何,都視作“相似”。即“餘弦相
推薦演算法之Jaccard相似度與Consine相似度
0-- 前言:對於個性化推薦來說,最核心、重要的演算法是相關性度量演算法。相關性從網站物件來分,可以針對商品、使用者、旺鋪、資訊、類目等等,從計算方式看可以分為文字相關性計算和行為相關性計算,具體的實現方法有很多種,最常用的方法有餘弦夾角(Cosine)方法、傑卡德(Jacc
文字相似度計算的幾個距離公式(歐氏距離、餘弦相似度、Jaccard距離、編輯距離)
本文主要講一下文字相似度計算的幾個距離公式,主要包括:歐氏距離、餘弦相似度、Jaccard距離、編輯距離。 距離計算在文字很多場景下都可以用到,比如:聚類、K近鄰、機器學習中的特徵、文字相似度等等。接下來就一一介紹一下: 假設兩個文字X=(x1, x2, x3,...xn)
LeetCode之計算字串相似度或編輯距離EditDistance
問題描述: /** * Given two words word1 and word2, find the minimum number of steps required to * convert word1 to word2. (each oper
歐式距離與餘弦相似度
歐氏距離 在歐幾里得空間裡面,點x =(x1,…,xn)和 y =(y1,…,yn)的歐幾里得距離為: 歐幾里得距離關注的是同一個維度裡面,數值之間的差異。當不同維度的刻度差異較大,比如身高(m)和體重(kg),如果使用這兩個單位,歐式距離的變現出來的差
距離和相似度度量
com 聚類算法 匯總 pearson 求和 選擇 方式 獲得 分享 在數據分析和數據挖掘的過程中,我們經常需要知道個體間差異的大小,進而評價個體的相似性和類別。最常見的是數據分析中的相關分析,數據挖掘中的分類和聚類算法,如K最近鄰(KNN)和K均值(K-Means)。當然
基於編輯距離來判斷詞語相似度方法(scala版)
使用 ref ray 只需要 art 算法 位置 spark else 詞語相似性比較,最容易想到的就是編輯距離,也叫做Levenshtein Distance算法。在Python中是有現成的模塊可以幫助做這個的,不過代碼也很簡單,我這邊就用scala實現了一版。 編輯
演算法之常用的距離和相似度度量
在資料分析和資料探勘的過程中,我們經常需要知道個體間差異的大小,進而評價個體的相似性和類別。最常見的是資料分析中的相關分析,資料探勘中的分類和聚類演算法,如K最近鄰(KNN)和K均值(K-Means)。當然衡量個體差異的方法有很多,這裡整理羅列下。 為了方便下面的解釋和舉例,先設定我們要
基於WMD(詞移距離)的句子相似度分析簡介
word2vec word2vec是隻有一個隱層的全連線神經網路,對語料中的所有詞彙進行訓練並生成相應的詞向量(Word Embedding)WI 的大小是VxN, V是單詞字典的大小, 每次輸入是一個單詞, N是設定的隱層大小。word2vec的模型通過一種神經網路語言模型(Neu
Opencv媒體與GUI---OpenCV的視訊輸入和相似度測量
程式碼 #include <iostream> // for standard I/O #include <string> // for strings #include <iomanip> // for controlling f
字串相似度演算法(編輯距離演算法 Levenshtein Distance)
在搞驗證碼識別的時候需要比較字元程式碼的相似度用到“編輯距離演算法”,關於原理和C#實現做個記錄。 據百度百科介紹: 編輯距離,又稱Levenshtein距離(也叫做Edit Distance),是指兩個字串之間,由一個轉成另一個所需的最少編輯操作次數,如果它們的距離越大,說明它們越是不同。許可
資料相似度處理功能實現思路與方法
最近接到一個需求,需求直接來源於業務的一句話,“找出這堆商品資訊裡面相似的商品,根據名稱判斷”。需求看似簡單,實則思考起來用技術實現是需要花點心思的。對於這樣的需求,首先要有一個思路和思考的過程:1、業務具體想要的是什麼? -- 名稱相似度超過一定比例的兩個商品可以算成一個或
相似度/距離方法總結
假設兩個向量 歐式距離:
18種和“距離(distance)”、“相似度(similarity)”相關的量的小結
在計算機人工智慧領域,距離(distance)、相似度(similarity)是經常出現的基本概念,它們在自然語言處理、計算機視覺等子領域有重要的應用,而這些概念又大多源於數學領域的度量(metric)
演算法介紹(3) 編輯距離演算法-字串相似度
編輯距離,又稱Levenshtein距離,是指兩個字串之間,由一個轉成另一個所需的最少編輯操作次數。 具體的操作方法為:
相似度演算法之歐幾里得距離
在計算使用者相似度的過程中,歐幾里得距離是比較直觀,常見的一種相似度演算法。 根據兩使用者之間共同評價的Item為維度,建立一個多維的空間,那麼通過使用者對單一維度上的評價Score組成的座標系X(s1,s2,s3……,si)即可定位該使用者在這個多維度空間中的位置,那麼