作者：咚懂咚懂咚
連結：https://zhuanlan.zhihu.com/p/22445302
來源：知乎
著作權歸作者所有。商業轉載請聯絡作者獲得授權，非商業轉載請註明出處。

之前曾經寫過一篇關於小波變換的回答（能不能通俗的講解下傅立葉分析和小波分析之間的關係？ - 咚懂咚懂咚的回答），得到很多贊，十分感動。之後一直說要更新，卻不知不覺拖了快一年。。此次更新，思來想去，決定挑戰一下壓縮感知（compressed sensing, CS）這一題目。

在我看來，壓縮感知是訊號處理領域進入21世紀以來取得的最耀眼的成果，並在磁共振成像、影象處理等領域取得了有效應用。壓縮感知理論在其複雜的數學表述背後蘊含著非常精妙的思想。基於一個有想象力的思路，輔以嚴格的數學證明，壓縮感知實現了神奇的效果，突破了訊號處理領域的金科玉律——奈奎斯特取樣定律。即，在訊號取樣的過程中，用很少的取樣點，實現了和全取樣一樣的效果。

正是被它的精妙思想所打動，我選擇它作為專欄第二篇的主題。理解壓縮感知的難度可能要比之前講的小波還要大，但是我們從中依然可以梳理出清晰的脈絡。這篇文章的目標和之前一樣，我將拋棄複雜的數學表述，用沒有公式的語言講清楚壓縮感知的核心思路，儘量形象易懂。我還繪製了大量示意圖，因為排版問題，我將主要以PPT的形式呈現，並按slice標好了序號。

---------------------------------------------------------------------------------------------------------------------------

一、什麼是壓縮感知（CS）？

compressed sensing又稱compressed sampling，似乎後者看上去更加直觀一些。沒錯，CS是一個針對訊號取樣的技術，它通過一些手段，實現了“壓縮的取樣”，準確說是在取樣過程中完成了資料壓縮的過程。

因此我們首先要從訊號取樣講起：

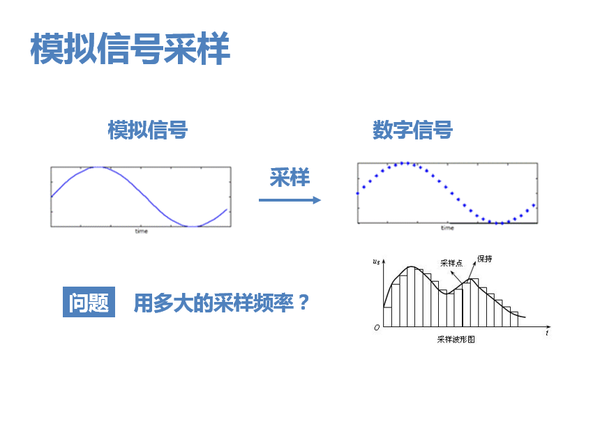
1. 我們知道，將模擬訊號轉換為計算機能夠處理的數字訊號，必然要經過取樣的過程。問題在於，應該用多大的取樣頻率，即取樣點應該多密多疏，才能完整保留原始訊號中的資訊呢？

---------------------------------------

2. 奈奎斯特給出了答案——訊號最高頻率的兩倍。一直以來，奈奎斯特取樣定律被視為數字訊號處理領域的金科玉律。

---------------------------------------

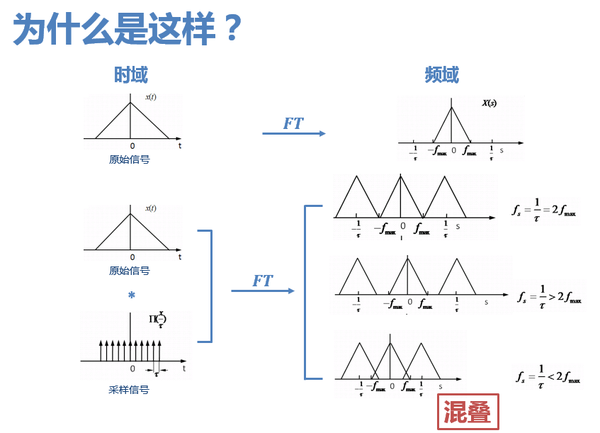3. 至於為什麼是兩倍，學過訊號處理的同學應該都知道，時域以τ為間隔進行取樣，頻域會以1/τ為週期發生週期延拓。那麼如果取樣頻率低於兩倍的訊號最高頻率，訊號在頻域頻譜搬移後就會發生混疊。

---------------------------------------

4. 然而這看似不容置疑的定律卻受到了幾位大神的挑戰。Candes最早意識到了突破的可能，並在不世出的數學天才陶哲軒以及Candes的老師Donoho的協助下，提出了壓縮感知理論，該理論認為：如果訊號是稀疏的，那麼它可以由遠低於取樣定理要求的取樣點重建恢復。

---------------------------------------

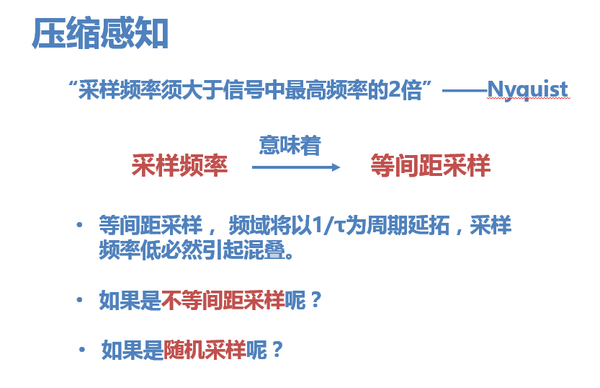5. 而突破的關鍵就在於取樣的方式。當我們說“取樣頻率”的時候，意味著做的是等間距取樣，數字訊號領域通常都是做等間距取樣，也服從奈奎斯特取樣定律。

但是如果是不等間距取樣呢？依然必須要服從取樣定理嗎？

---------------------------------------

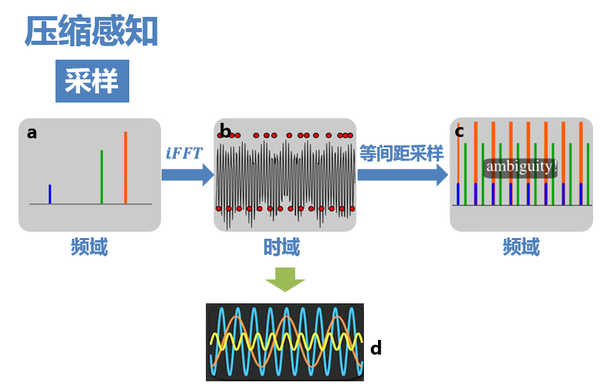
6. 答案是，隨機的亞取樣給了我們恢復原訊號的可能。

上圖非常關鍵，它可以簡單直觀地表述壓縮感知的思路。 如圖b、d為三個餘弦函式訊號疊加構成的訊號，在頻域的分佈只有三條線（圖a）。 如果對其進行8倍於全取樣的等間距亞取樣（圖b下方的紅點），則頻域訊號週期延拓後，就會發生混疊（圖c），無法從結果中復原出原訊號。

---------------------------------------

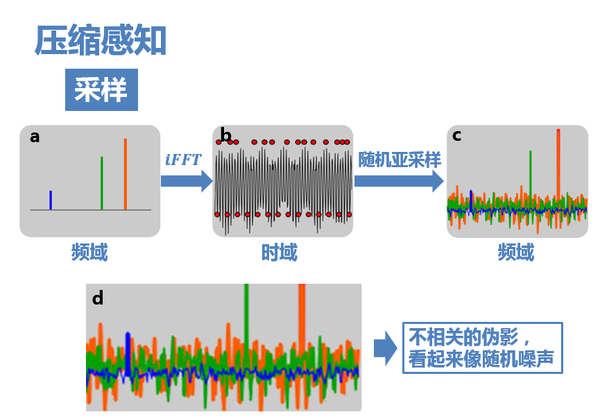7. 而如果採用隨機亞取樣（圖b上方的紅點），那麼這時候頻域就不再是以固定週期進行延拓了，而是會產生大量不相關（incoherent）的干擾值。如圖c，最大的幾個峰值還依稀可見，只是一定程度上被幹擾值覆蓋。這些干擾值看上去非常像隨機噪聲，但實際上是由於三個原始訊號的非零值發生能量洩露導致的（不同顏色的干擾值表示它們分別是由於對應顏色的原始訊號的非零值洩露導致的）

P.S：為什麼隨機亞取樣會有這樣的效果？

這可以理解成隨機取樣使得頻譜不再是整齊地搬移，而是一小部分一小部分胡亂地搬移，頻率洩露均勻地分佈在整個頻域，因而洩漏值都比較小，從而有了恢復的可能。

---------------------------------------

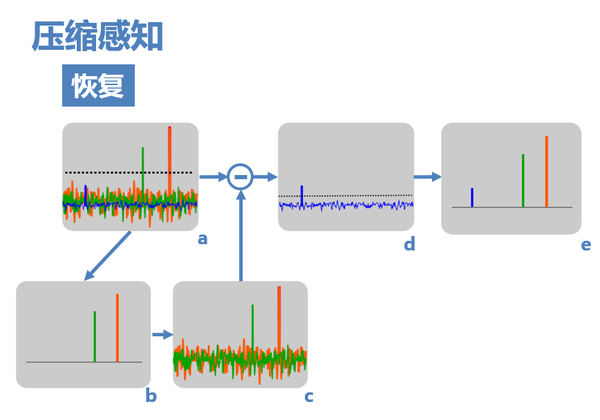
8. 接下來的關鍵在於，訊號該如何恢復？ 下面講一種典型的演算法（匹配追蹤）：

(1) 由於原訊號的頻率非零值在亞取樣後的頻域中依然保留較大的值，其中較大的兩個可以通過設定閾值，檢測出來（圖a）。

(2) 然後，假設訊號只存在這兩個非零值（圖b），則可以計算出由這兩個非零值引起的干擾（圖c）。

(3) 用a減去c，即可得到僅由藍色非零值和由它導致的干擾值(圖d），再設定閾值即可檢測出它，得到最終復原頻域（圖e）

(4) 如果原訊號頻域中有更多的非零值，則可通過迭代將其一一解出。

以上就是壓縮感知理論的核心思想——以比奈奎斯特取樣頻率要求的取樣密度更稀疏的密度對訊號進行隨機亞取樣，由於頻譜是均勻洩露的，而不是整體延拓的，因此可以通過特別的追蹤方法將原訊號恢復。

二、壓縮感知的前提條件

接下來我們總結一下，能實現壓縮感知的關鍵在於什麼，即需要哪些前提條件。

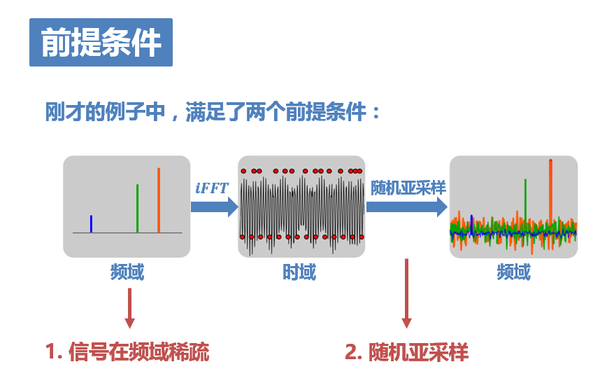9. 在剛才的講述中大家可以感受到，這個例子之所以能夠實現最終訊號的恢復，是因為它滿足了兩個前提條件：

1. 這個訊號在頻域只有3個非零值，所以可以較輕鬆地恢復出它們。

2. 採用了隨機亞取樣機制，因而使頻率洩露均勻地分佈在整個頻域。

這兩點對應了CS的兩個前提條件——稀疏性（sparsity）、不相關性（incoherence）。

---------------------------------------

10. 關於稀疏性可以這樣簡單直觀地理解：若訊號在某個域中只有少量非零值，那麼它在該域稀疏，該域也被稱為訊號的稀疏域。

因此，第一個前提條件要求訊號必須在某一個變換域具有稀疏性。比如例子中，訊號在頻域是稀疏的，因而可以通過所述的重建方法輕鬆地在稀疏域（頻域）復原出原訊號。

---------------------------------------

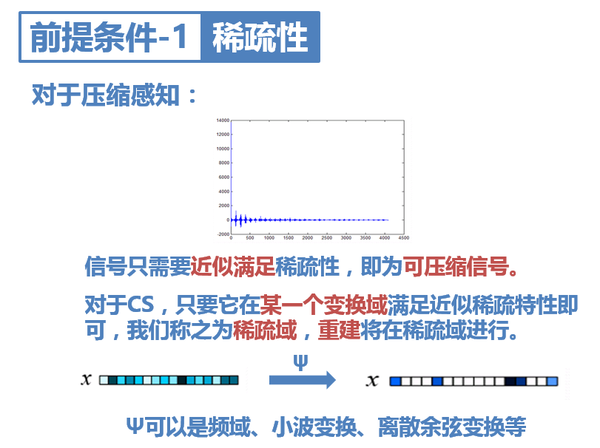
然而通常訊號在變換域中不會呈現完全的稀疏性。其實只要它近似滿足稀疏性，即大部分值趨於零，只有少量大的非零值，就可以認為它是可壓縮訊號，可以對它進行CS亞取樣。

對於之前講的例子，如果它在頻域中不稀疏，我們可以做DWT、DCT等，找到它的稀疏變換。

---------------------------------------

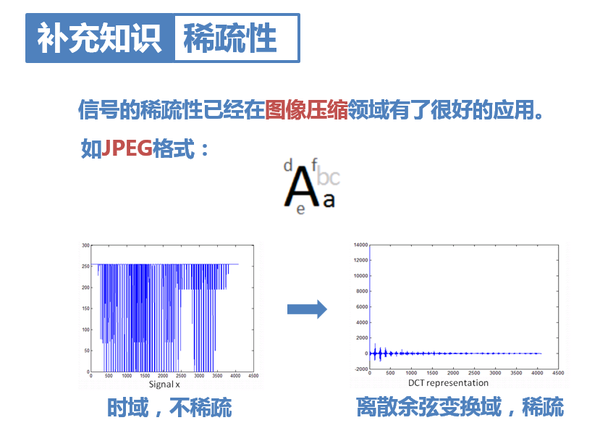
11. 這裡針對訊號的稀疏性和訊號壓縮額外補充一下：其實，訊號的稀疏性已經在影象壓縮領域有了很廣泛的應用。利用訊號的稀疏性，可以對訊號進行壓縮。如影象壓縮領域的JPEG格式，就是將影象變換到離散餘弦域，得到近似稀疏矩陣，只保留較大的值，從而實現壓縮。

---------------------------------------

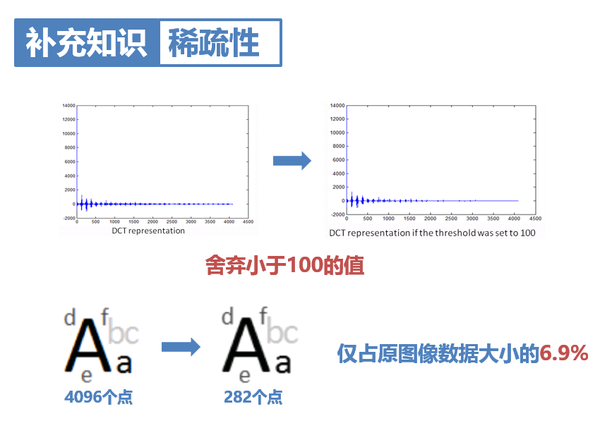
12. 比如這個例子中，僅用原影象6.9%的點就復原了和原影象基本相同的影象。我們還可以採用小波變換，即為JPEG-2000，壓縮效果更好。

---------------------------------------

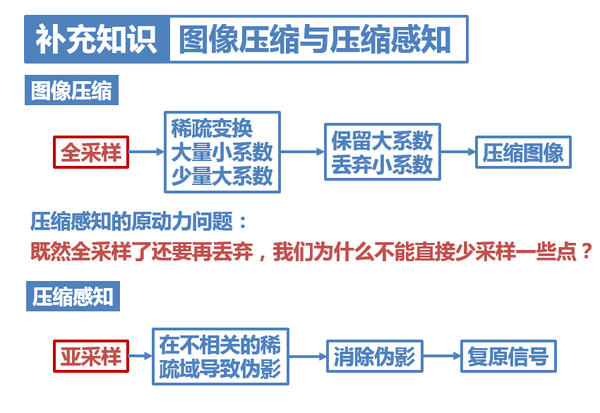
13. 這裡需要指出，影象壓縮和壓縮感知這兩個概念很容易弄混，大家一定要分清。

它們其實有著本質上的區別。影象壓縮是先進行了全取樣，然後再變換域丟棄小系數，完成壓縮；

而壓縮感知不同，它的思想其實從影象壓縮中借鑑了很多：既然全取樣了還要再丟棄，我們為什麼不能直接少採樣一些點？因此，壓縮感知直接進行了亞取樣，然後再用演算法消除亞取樣導致的偽影。可以說，壓縮感知直接在取樣時就完成了壓縮。

---------------------------------------

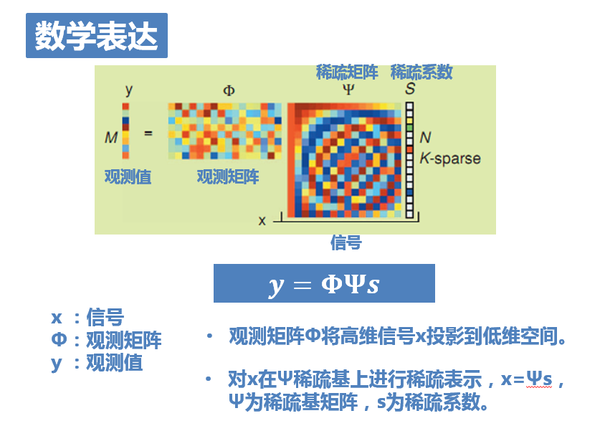
14. 接下來，在將第二個前提條件之前，還是需要引入必要的數學表達的。上圖是一個大家在壓縮感知相關的書籍文獻中會經常看到的一張示意圖。很多文章試圖用這張圖給大家講清楚什麼是壓縮感知，結果導致大家看得一頭霧水，混淆在各種“矩陣”當中。。不過相信有了我之前的講解，現在這張圖會好理解很多。這張圖也就是把亞取樣的過程用矩陣的方式表達出來而已：

如圖，x是為長度N的一維訊號，也就是原訊號，稀疏度為k。此刻它是未知的。

Φ為觀測矩陣，對應著亞取樣這一過程。它將高維訊號x投影到低維空間，是已知的。

y=Φx為長度M的一維測量值，也就是亞取樣後的結果。顯然它也是已知的。

因此，壓縮感知問題就是在已知測量值y和測量矩陣Φ的基礎上，求解欠定方程組y=Φx得到原訊號x。

然而，一般的自然訊號x本身並不是稀疏的，需要在某種稀疏基上進行稀疏表示。令x=Ψs，Ψ為稀疏基矩陣，s為稀疏係數。

於是最終方程就變成了：y=ΦΨs。已知y、Φ、Ψ，求解s。

---------------------------------------

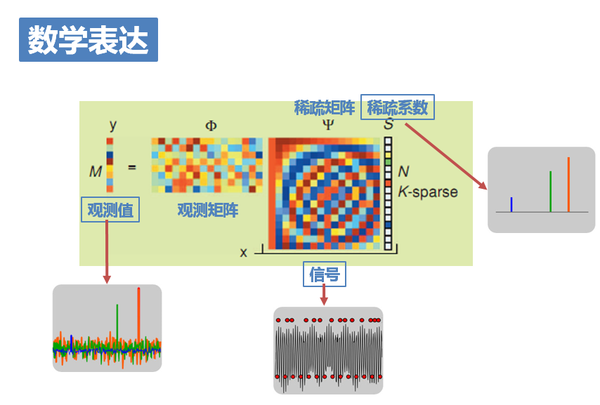
15. 對應一開始的例子大家就能明白：x就是三個正弦訊號疊加在一起的原訊號；稀疏矩陣Ψ就是傅立葉變換，將訊號變換到頻域S；而觀測矩陣Φ就對應了我們採用的隨機亞取樣方式；y就是最終的取樣結果。

---------------------------------------

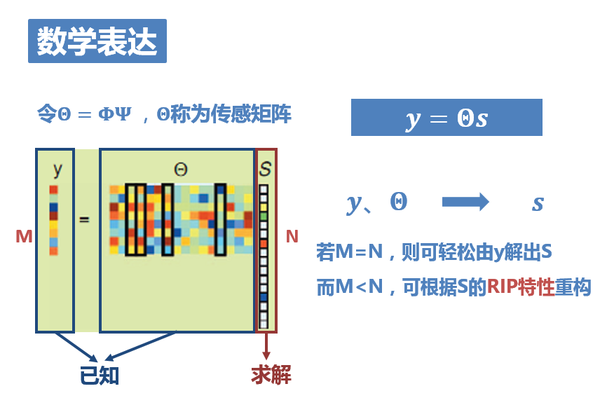16. y=ΦΨs有點長，我們把ΦΨ合併成一個矩陣，稱之為感測矩陣。即令Θ=ΦΨ，則y=ΘS。

問題即為，已知y和Θ，求解S。

求解出S後，由x=Ψs即可得到恢復出的原訊號x。

然而在正常情況下，方程的個數遠小於未知數的個數，方程是沒有確定解的，無法重構訊號。但是，由於訊號是K稀疏，如果上式中的Φ滿足有限等距性質(RIP)，則K個係數就能夠從M個測量值準確重構（得到一個最優解）。

---------------------------------------

17.接下來的數學內容可以簡短略過：陶大神和Candès大神證明了RIP才是觀測矩陣要滿足的準確要求。但是，要確認一個矩陣是否滿足RIP非常複雜。於是Baraniuk證明：RIP的等價條件是觀測矩陣和稀疏表示基不相關（incoherent）。

這就是壓縮感知的第二個前提條件。

---------------------------------------

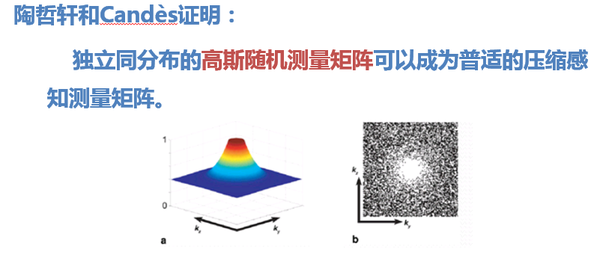
18. 那怎樣找到不相關的觀測矩陣呢？陶哲軒和Candès又證明： 獨立同分布的高斯隨機測量矩陣可以成為普適的壓縮感知測量矩陣。

於是滿足高斯分佈的隨機測量矩陣就成了CS最常用的觀測矩陣。

對於二維訊號，往往就採用如右上圖所示的取樣矩陣對影象進行亞取樣。

對於一維訊號，採用前文提到的隨機不等間距的亞取樣即可。

------------------------------------------------------------------------------

到這裡，我們可以這樣用一句話概括地描述什麼是壓縮感知：

如果一個訊號在某個變換域是稀疏的，那麼就可以用一個與變換基不相關的觀測矩陣將變換所得高維訊號投影到一個低維空間上，然後通過求解一個優化問題就可以從這些少量的投影中以高概率重構出原訊號。

以上可以算作是壓縮感知的定義吧。但是如果要再簡潔一點呢？

在我看來，壓縮感知可以用這樣一句話來表述：

直接採集出一個JPEG

——之前影象壓縮的方法是全取樣之後再壓縮，拋棄稀疏變換域中的一些小系數；而CS直接減少了取樣點，採集完後、經過重建的影象，就是一副在某變換域稀疏的壓縮影象，比如JPEG。

那這麼做有什麼優勢呢？

對於很多情形，比如照相機拍攝照片，這樣減少採樣點並沒有優勢。因為所有畫素的採集在一瞬間就都完成了。

但是對於一些採集比較慢的情形，比如核磁共振成像，CS就可以發揮巨大優勢。原本一副MRI影象常常需要幾十秒，速度慢也是MRI的一大缺陷。而應用CS技術後，只需要採集全取樣幾分之一的資料，就可以重建出原圖。這樣就可以把成像速度提高好幾倍，同時對影象質量影響不大。

另一個應用是Rice大學開發的單畫素相機，也就是說這種相機只需要一個畫素，非常有趣。感興趣的朋友可以自己去調查。

三、壓縮感知的重建方法

如前文所述，CS的重建也就是求解欠定方程組y=ΘS的方法。這是一個零範數（l0）最小化問題，是一個NP完全問題（沒有快速解法的問題），因此往往轉換成一範數（l1）最小化的求解，或者用一些近似估計的演算法。這部分的具體內容在這裡就不再詳述了。

------------------------------------------------------------------------------

以上就是壓縮感知的簡單講述。各方面都只是淺嘗輒止，更多內容需還要大家自己研究。

其實寫這篇文章之前我已經做好了受冷落的準備，畢竟不像小波變換，壓縮感知的受眾面比較小，理解難度又比較大，大家閱讀時還請耐心一點。如果看後能對壓縮感知的主要思想有了一定的認識，也就不枉我費勁力氣畫了這麼多圖、碼了這麼多字。

注：未經允許，禁止微信公眾號轉載。

「原來還能打賞(⊙o⊙)」