1. 如果陣列中部分元素已按自然數順序排放，例如，陣列
   

，則初期自然排好序的子陣列段顯然有4段，分別為

，

，

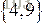
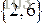
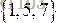
和

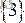
。請充分利用上述特點設計並實現一個自然合併排序演算法。
(1) 演算法設計思路
先對陣列進行一次線性掃描，記錄下部分有序陣列的斷開位置和個數，個數用於判斷最後一個斷開的位置是否為陣列末尾，位置用於合併陣列。迴圈-依次將相鄰的兩兩陣列進行合併，直到最後剩下一個陣列，即為合併排序好的陣列。

(2) 演算法實現的虛擬碼
功能描述：對陣列進行線性掃描，記錄下該斷點的位置和斷點個數
輸入：陣列大小n
輸出：陣列劃分後的斷點個數+1

    int fenduan(int n)
    int j=0;
    rem[j++]=0
    for i=0 to n-2
    if (arr[i]>arr[i+1]) rem[j]=i;j++;//記錄斷點的位置
    end for 
    rem[j++]=n-1;
    return j;

功能描述:通過記錄的斷點位置將兩兩相鄰的偽陣列進行合併排序
輸入：起始位置a，斷點位置m，終點位置r
輸出：

    void merge(int a,int m,int r)
    int i=a,j=m+1,k=a;
    while (i<=m&&j<=r)
    if
 
 (arr[i]<=arr[j]) newarr[k++]=arr[i++]
    else newarr[k++]=arr[j++];
    end while
    if (i>m)
    for (int q=j to r) newarr[k++]=arr[q] end for 
    else for (int q=I to m) newarr[k++]=arr[q] end for 

功能描述:迴圈活動最終的自然合併排序
輸入：陣列的大小n
輸出：

    sort(int num)
    int a=huafen(num)
    while (a!=2
 
)
    for (int i=0 to a-1)
    if (i==0)
    merge(rem[i] ,rem[i+1], rem[i+2]);
    else if (i+2>a-1)
    merge(rem[i+1],rem[i+1],rem[i+1])
    else merge(rem[i]+1,rem[i+1],rem[i+2])
    end for
    /將合併好的陣列複製到原陣列
    for (int j=0;j<n;j++)
    arr[j]=newarr[j];end for 
    a=huafen(n);//繼續獲得斷點個數+1

(3) 實現程式碼

    import java.util.Scanner;
    public class main {
        static int[] arr;//建立錄入資料用的陣列
        static int[] newarr;//用於儲存合併後的陣列
        static int[] rem;//記錄陣列斷點的位置
        static int n;//陣列的大小

        //自然合併主方法
        static void sort(int num){
            int a=huafen(num);//斷點的個數+1
            while (a!=2){//如果只有一個斷點，則證明已經排好順序
                int i=0;            
                for (i=0;i<a-1;i+=2){
                    if (i==0)//對第一隊有序陣列進行排序
                        merge(rem[i] ,rem[i+1], rem[i+2]);
                    else if (i+2>a-1)//剩餘的部分有序陣列無法兩兩匹配
                        merge(rem[i+1],rem[i+1] , rem[i+1]);
                    else 
                        merge(rem[i]+1, rem[i+1], rem[i+2]);

    //              else if (i+2>a-1&&i+1==a-1)//最後兩個有序陣列兩兩合併
    //                  merge(rem[i], rem[i], rem[i+1]);
    //              else//有序陣列兩兩合併
    //                  merge(rem[i] ,rem[i+1], rem[i+2]);
                }
                //將合併好的陣列複製到原陣列
                for (int j=0;j<n;j++)
                    arr[j]=newarr[j];
                a=huafen(n);//繼續獲得斷點個數+1
            }
        }

        //劃分陣列的有序部分，並且記錄下該斷點的位置和斷點個數
        private static int huafen(int n) {
            int num=0;
            rem[num++]=0;
            for (int i=0;i<n-1;i++){
                if (arr[i]>arr[i+1])
                    rem[num++]=i;
            }
            rem[num++]=n-1;//將最後一個斷點位置賦值為陣列最後一個位置，便於排序
            return num;
        }   

        //進行合併排序
        private static void merge(int a, int m, int r) {
            int i=a;
            int j=m+1;
            int k=a;
            while (i<=m&&j<=r){
                if (arr[i]<=arr[j])
                    newarr[k++]=arr[i++];
                else {
                    newarr[k++]=arr[j++];
                }
            }
                if (i>m)
                    for (int q=j;q<=r;q++)
                        newarr[k++]=arr[q];
                else {
                    for (int q=i;q<=m;q++)
                        newarr[k++]=arr[q];
                }
        }

        public static void main(String []args){
            Scanner in=new Scanner(System.in);
            System.out.println("輸入陣列的大小");
            n=in.nextInt();
            //初始化資料
            newarr = new int[n];
            arr=new int[n];
            rem=new int[n+1];

            System.out.println("錄入資料，資料用空格格開");
            String line=in.nextLine();
            line=in.nextLine();
            String arrg[]=line.split(" ");
            for (int j=0;j<arrg.length;j++)
                arr[j]=Integer.parseInt(arrg[j]);   
            sort(n);
            System.out.println("自然合併排序後");
            for (int i=0;i<n;i++)
                System.out.print(newarr[i]+" ");
        }
    }

(4) 演算法執行結果及計算時間複雜度分析

時間複雜度為O(n)

(5) 體會
自然合併排序演算法比一般合併排序演算法多了一個掃描的方法。通過掃描後記錄斷點的位置和斷點的個數，可以很清晰的使用合併演算法來合併兩個相鄰的有序陣列斷。在每次的合併後，繼續掃描一次，然後再合併，直到掃描到只有一個斷點個數。在編寫程式碼的過程中，老是在迴圈遞迴合併演算法卡住了，不能很好的判斷要合併的相鄰的兩個陣列斷的起點，斷開的位置，和終點位置，導致耗費了比較多的時間

1. 最長公共子序列LCS問題：給定2個序列X和Y，當另一序列Z既是X的子序列又是Y的子序列時，稱Z是序列X和Y的公共子序列。給定X = {x1, x2, …, xm}和Y = {y1, y2, …, yn}，請找出X和Y的最長公共子序列。例如：
   輸入：X = ABCHFGASJKXBD Y = DBDHASXB
   輸出：LCS = BHASXB
   (1) 演算法設計思路
   建立二維陣列c儲存X和Y的最長公共子序列的長度，二維陣列b記錄c的值是由哪一個子問題解得到的，然後構造最長公共子序列。

(2) 演算法實現的虛擬碼
功能描述：建立備忘錄，記錄最長子序列的長度和對應所在位置
輸入：字串x，y和其長度n，m。備忘錄c，b
輸出：備忘錄c，b

    void max(int n,int m ,char[] x,char[] y,int[][] c,int[][] b)
    for(int I to n) c[i][0]=0
    for (int j to m) c[0][j]=0;
    for (int i to n)
    for (int j to m)
    if (x[i]=y[j])  c[i][j]=c[i-1][j-1]+1;b[i][j]=1;
    else if (c[i-1][j]>=c[i][j-1]) c[i][j]=c[i-1][j];b[i][j]=2; 
    else c[i][j]=c[i][j-1];b[i][j]=3;
    end for 
    end for

功能描述：使用備忘錄輸出共同的子序列
輸入：字串x和x的長度，y的長度。備忘錄b
輸出：最長公共子序列

        if (i==0||j==0)return;
        if (b[i][j]==1) input(i-1, j-1,x,b); 輸出(x[i]);
        else if (b[i][j]==2)input(i-1, j,x,b);
        else input(i, j-1,x,b);

(3) 實現程式碼

    package 演算法分析;

    import java.util.Scanner;

    public class main {
        //建立備忘錄，記錄所有的資料
        static void max(int n,int m,char[] x,char[] y,int[][] c,int[][] b){
            //初始化陣列
            for (int i=1;i<=n;i++)
                c[i][0]=0;
            for (int j=1;j<=m;j++)
                c[0][j]=0;
        /*
         * c[i][j]=① 0 ,i=0,j=0
         *          ②c[i]-1[j-1]+1 , Xi=Yj
         *          ③max{ (c[i][j-1],c[i-1][j]) } , Xi!=Yi
         */
            for (int i=1;i<=n;i++)
                for (int j=1;j<=m;j++){
                    if (x[i]==y[j]){
                        c[i][j]=c[i-1][j-1]+1;
                        b[i][j]=1;
                    }
                    else if (c[i-1][j]>=c[i][j-1]){
                        c[i][j]=c[i-1][j];
                        b[i][j]=2;
                    }
                    else {
                        c[i][j]=c[i][j-1];
                        b[i][j]=3;
                    }
                }
        }

        //使用備忘錄
        static void input(int i,int j,char[] x,int[][] b){
            if (i==0||j==0)
                return;
            if (b[i][j]==1){//如果Xi=Yj,遞迴，輸出該值
                input(i-1, j-1,x,b);
                System.out.print(x[i]);
            }
            else if (b[i][j]==2){
                input(i-1, j,x,b);
            }
            else 
                input(i, j-1,x,b);
        }

        public static void main(String []args){
            Scanner in=new Scanner(System.in);
            System.out.println("輸入字串x[]");
            String line=in.nextLine();
            char[] x;
            x=line.toCharArray();
            int n=x.length;//獲取字串x的長度
            //為x頭加上空格
            char c1[]=null;
            c1=x;
            x=new char[n+1];
            x[0]=' ';
            for (int i=1;i<=n;i++)
                x[i]=c1[i-1];
            System.out.println("輸入字串Y[]");
            String line2=in.nextLine();
            char[] y;
            y=line2.toCharArray();
            int m=y.length;//獲取字串y的長度
            //為字串y頭加上空格
            char c2[]=null;
            c2=y;
            y=new char[m+1];
            y[0]=' ';
            for (int i=1;i<=m;i++)
                y[i]=c2[i-1];

            int[][] c=new int[n+1][m+1];
            int[][] b=new int[n+1][m+1];

            max(n, m, x, y, c, b);
            input(n, m, x, b);
        }
    }

(4) 演算法執行結果及計算時間複雜度分析

O(mn)+O(n+m)
(5) 體會
重在理解。備忘錄的使用非常的巧妙，經常會忘記使用備忘錄而導致結果錯誤。使用動態規劃的時候，先找出最優解的性質，並刻畫其結構特徵，然後遞迴定義最優解，再自底而上的方式計算最優值，最後根據計算最優值時得到的資訊，構造最優解。分析最優解的性質很重要，也比較有難度。通過做這道題，發現我現在對動態規劃的理解還差得遠呢，但是隻要肯努力，就沒有什麼不可能。