機器學習各個演算法---1.線性迴歸
阿新 • • 發佈:2019-01-22
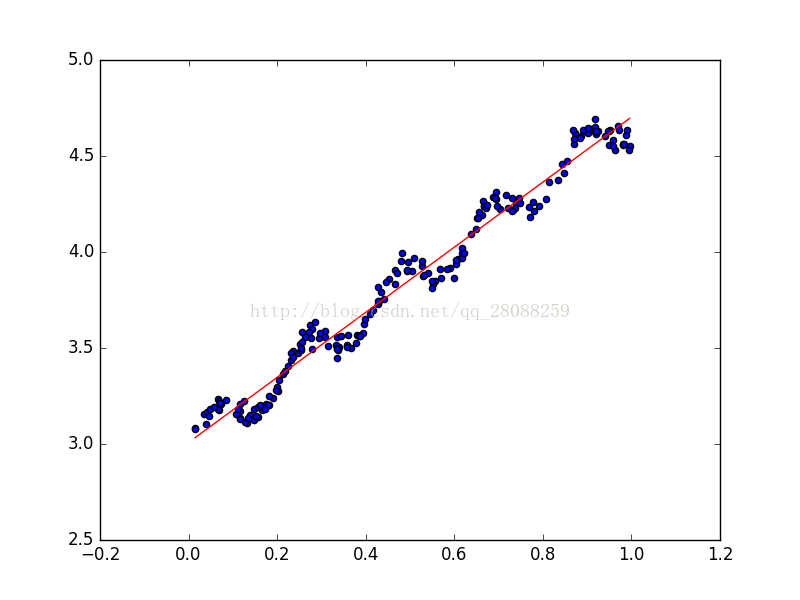
1.最原始的linear regression
標準迴歸函式和文字資料匯入函式
測試from numpy import * def loadDataSet(fileName): #general function to parse tab -delimited floats numFeat = len(open(fileName).readline().split('\t')) - 1 #get number of fields '\t'是tab,每一行的特徵個數 dataMat = []; labelMat = [] #資料矩陣,標籤矩陣 fr = open(fileName) for line in fr.readlines(): #fr.readlines()表示讀取每一行 lineArr =[] #該行的列表,注意這裡儲存的可是數字了 curLine = line.strip().split('\t') #strip()去掉前後的空格,split()把一個字串分割成字串陣列 for i in range(numFeat): #數字序列,內建函式range() range(10) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9] lineArr.append(float(curLine[i])) # dataMat.append(lineArr) labelMat.append(float(curLine[-1])) #-1表示倒數第一個 return dataMat,labelMat #返回資料矩陣和標籤矩陣(目標值矩陣) def standRegres(xArr,yArr): #用來計算最佳擬合直線 xMat = mat(xArr); yMat = mat(yArr).T #搞成矩陣形式 matrix.T transpose:返回矩陣的轉置矩陣 xTx = xMat.T*xMat if linalg.det(xTx) == 0.0: # numpy.linalg模組包含線性代數的函式,計算行列式值是否為0 print "This matrix is singular, cannot do inverse" #奇異矩陣 return ws = xTx.I * (xMat.T*yMat) #matrix.I inverse:返回矩陣的逆矩陣,就這一步就求出來了,該演算法叫做普通最小二乘法(ordinary least squares) return ws
結果:import regression import matplotlib.pyplot as plt from numpy import * xArr, yArr = regression.loadDataSet('ex0.txt') # print xArr[0:2] #取不到2 # print yArr #接下來來看擬合的效果 ws = regression.standRegres(xArr, yArr) # print ws #變數ws存放的就是迴歸係數 xMat = mat(xArr) yMat = mat(yArr) yHat = xMat*ws #計算預測值 #接下來繪製資料集散點圖和最佳擬合直線圖 fig = plt.figure() ax = fig.add_subplot(111) ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0]) # flatten()方法能將matrix的元素變成一維的, # .A能使matrix變成array xCopy = xMat.copy() # print xCopy xCopy.sort(0) #按照升序排序,主要是根據第二個元素 # print xCopy yHat = xCopy *ws ax.plot(xCopy[:,1],yHat,'red') plt.show()
2. locally weighted linear regression
必要函式
測試#以下函式,對於x空間中的任意一個testPoint,輸出其對應的預測值yHat def lwlr(testPoint,xArr,yArr,k=1.0): # 引數k控制衰減速度 1.0為預設值; testPoint為輸入,函式返回根據區域性加權線性迴歸得出的預測值 xMat = mat(xArr); yMat = mat(yArr).T m = shape(xMat)[0] #[0]指示的是行數,也就是樣本點個數 weights = mat(eye((m))) #eye(m)主對角元素為1----對應於(m,m),其餘為0 for j in range(m): #next 2 lines create weights matrix diffMat = testPoint - xMat[j,:] weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) xTx = xMat.T * (weights * xMat) if linalg.det(xTx) == 0.0: print "This matrix is singular, cannot do inverse" return ws = xTx.I * (xMat.T * (weights * yMat)) return testPoint * ws def lwlrTest(testArr,xArr,yArr,k=1.0): #loops over all the data points and applies lwlr to each one, k的預設值為1 m = shape(testArr)[0] yHat = zeros(m) #元素全為0的向量 for i in range(m): yHat[i] = lwlr(testArr[i],xArr,yArr,k) return yHat def lwlrTestPlot(xArr,yArr,k=1.0): #same thing as lwlrTest except it sorts X first yHat = zeros(shape(yArr)) #easier for plotting xCopy = mat(xArr) xCopy.sort(0) for i in range(shape(xArr)[0]): yHat[i] = lwlr(xCopy[i],xArr,yArr,k) return yHat,xCopy
import regression
import matplotlib.pyplot as plt
from numpy import *
xArr, yArr = regression.loadDataSet('ex0.txt')
# print yArr[0]
# print regression.lwlr(xArr[0],xArr,yArr,0.001)
yHat, xSort = regression.lwlrTestPlot(xArr,yArr,1) #此處的這個k值得選取會直接影響到擬合的效果
# print xSort
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(xSort[:,1],yHat)
xMat = mat(xArr)
yMat = mat(yArr)
ax.scatter(xMat[:,1].flatten().A[0],yMat.T[:,0].flatten().A[0], s=2, c='red')
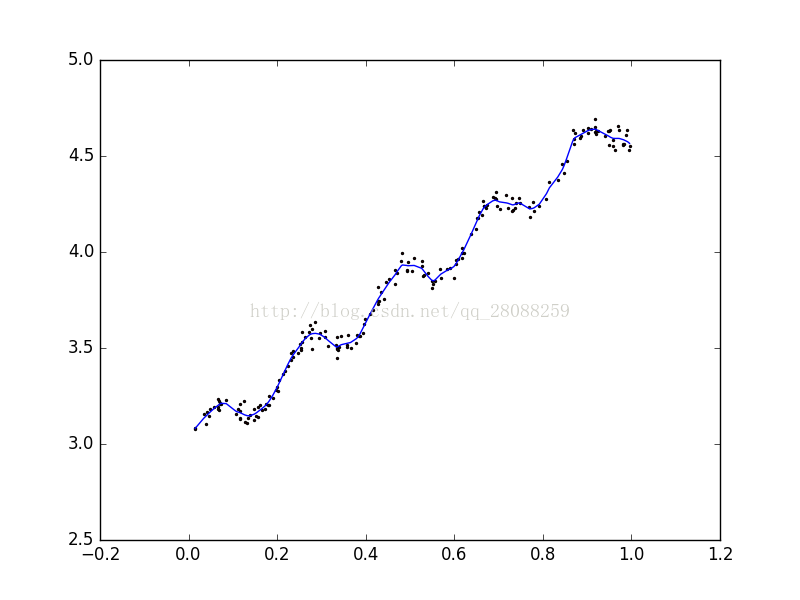
plt.show() k=1 欠擬合
k=0.01
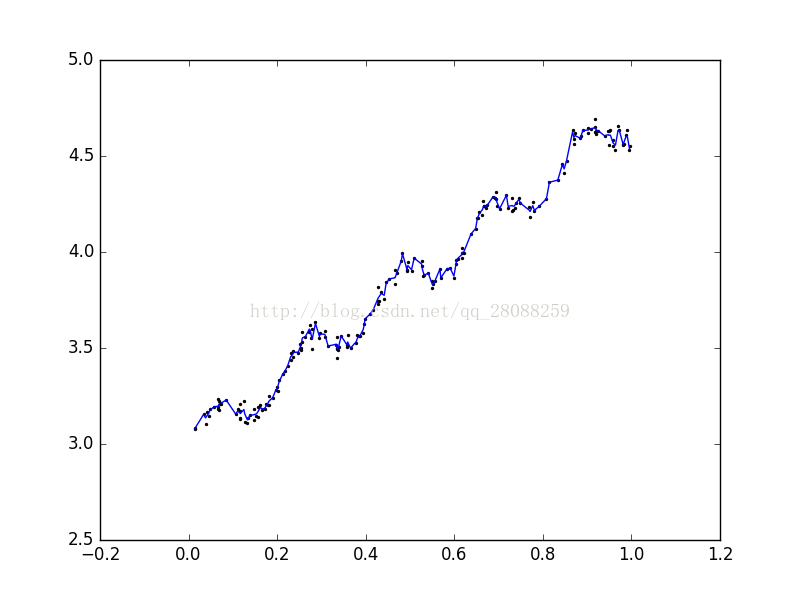
k=0.003 過擬合
3. 預測鮑魚的年齡
#預測鮑魚年齡
import regression
from numpy import *
abX, abY = regression.loadDataSet('abalone.txt')
yHat01=regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],0.1) #過擬合
yHat1=regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],1)
yHat10=regression.lwlrTest(abX[0:99],abX[0:99],abY[0:99],10)
print regression.rssError(abY[0:99], yHat01.T)
print regression.rssError(abY[0:99], yHat1.T)
print regression.rssError(abY[0:99], yHat10.T)
yHat01New=regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],0.1) #過擬合
yHat1New=regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],1)
yHat10New=regression.lwlrTest(abX[100:199],abX[0:99],abY[0:99],10)
print regression.rssError(abY[100:199], yHat01New.T)
print regression.rssError(abY[100:199], yHat1New.T)
print regression.rssError(abY[100:199], yHat10New.T)
#接下里看看普通的線性迴歸
ws = regression.standRegres(abX[0:99], abY[0:99])
yHat =mat(abX[100:199])*ws
print regression.rssError(abY[100:199],yHat.T.A)56.8843765879
429.89056187
549.118170883
58720.7256135
573.526144189
517.571190538
518.636315325
4. 縮減係數來“理解”資料
4.1 嶺迴歸
#嶺迴歸---在鮑魚資料集上的效果
import regression
from numpy import *
import matplotlib.pyplot as plt
abX, abY = regression.loadDataSet('abalone.txt')
ridgeWeights = regression.ridgeTest(abX, abY)
print ridgeWeights
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights)
plt.show()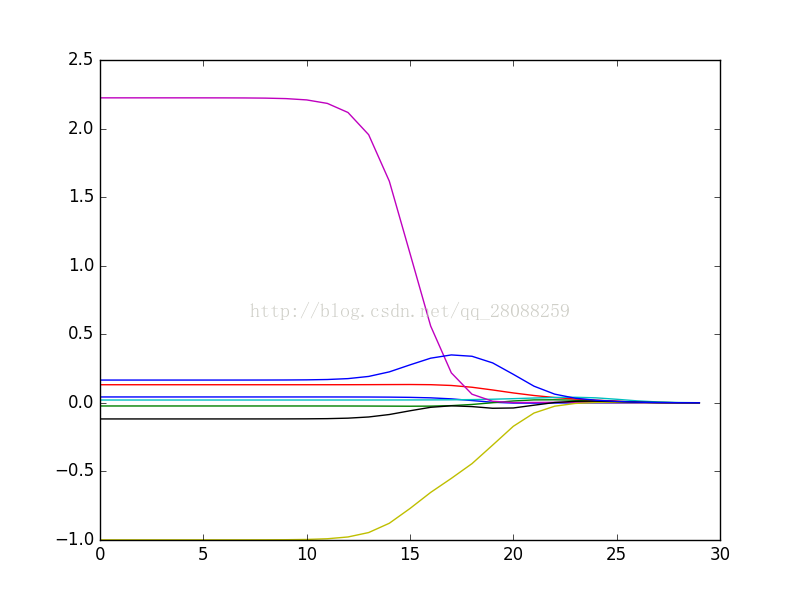
4.2 前向逐步迴歸
def regularize(xMat):#regularize by columns
inMat = xMat.copy()
inMeans = mean(inMat,0) #calc mean then subtract it off
inVar = var(inMat,0) #calc variance of Xi then divide by it
inMat = (inMat - inMeans)/inVar
return inMat
def stageWise(xArr,yArr,eps=0.01,numIt=100): #前向逐步線性迴歸
xMat = mat(xArr); yMat=mat(yArr).T
yMean = mean(yMat,0)
yMat = yMat - yMean #can also regularize ys but will get smaller coef
xMat = regularize(xMat)
m,n=shape(xMat)
returnMat = zeros((numIt,n)) #testing code remove
ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy()
for i in range(numIt): #numIt表示迭代次數
print ws.T
lowestError = inf; #inf表示無窮
for j in range(n):
for sign in [-1,1]: #分別顯示增加和減少該特徵係數對結果的影響
wsTest = ws.copy()
wsTest[j] += eps*sign
yTest = xMat*wsTest
rssE = rssError(yMat.A,yTest.A)
if rssE < lowestError:
lowestError = rssE
wsMax = wsTest
ws = wsMax.copy()
returnMat[i,:]=ws.T
return returnMat測試
#測試前向逐步線性迴歸的效果
import regression
from numpy import *
import matplotlib.pyplot as plt
xArr, yArr = regression.loadDataSet('abalone.txt')
print regression.stageWise(xArr,yArr,0.001,5000)
#將其結果與最小二乘法進行比較
xMat = mat(xArr)
yMat = mat(yArr).T
xMat = regression.regularize(xMat)
yM = mean(yMat,0)
yMat = yMat - yM
weights=regression.standRegres(xMat, yMat.T)
print weights.T