手把手教你搭建卷積神經網路(CNN)
本文是基於吳恩達老師的《深度學習》第四課第一週習題所做,如果本文在某些知識點上描述得不夠透徹的可以參見相關章節的具體講解,同時極力推薦各位有志從事計算機視覺的朋友觀看一下吳恩達老師的《深度學習》課程。
1.卷積神經網路構成
總的來說,卷積神經網路與神經網路的區別是增加了若干個卷積層,而卷積層又可細分為卷積(CONV)和池化(POOL)兩部分操作(這兩個重要概念稍後會簡單的介紹,如果對CNN的基本概念不是特別瞭解的同學可以學習達叔的《卷積神經網路》課程);然後是全連線層(FC),可與神經網路的隱藏層相對應;最後是softmax層預測輸出值y_hat。下圖為CNN的結構圖。
雖然深度學習框架會讓這種複雜的演算法實現起來變得容易,但只有自己實現一遍才能更透徹的理解上圖中涉及到的計算操作。因此,本文先按照上圖卷積神經網路的運算步驟,通過編寫函式一步一步來實現CNN模型,最後會使用TensorFlow框架搭建CNN來進行圖片分類。
2.第三方庫
以下是在編碼實現CNN中用到的第三方庫。
import numpy as np
import h5py
import matplotlib.pyplot as plt
plt.rcParams['figure.figsize'] = (5.0,4.0)
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
np.random.seed(1)3.前向傳播過程
卷積神經網路的前向傳播過程包括:填充(padding)、卷積操作(conv)、啟用函式(Relu)、池化(pooling)、全連線(FC)、softmax分類,其中啟用、全連線、softmax與深層神經網路中的計算方法一致,本文不再贅述,如不瞭解可參見本人上一篇文章《
3.1 填充(padding)
對輸入影象進行卷積操作時,我們會發現一個問題:角落或邊緣的畫素點被使用的次數相對較少。這樣一來在圖片識別中會弱化邊緣資訊。因此我們使用padding操作,在影象原始資料周圍填充p層資料,如下圖。當填充的資料為0時,我們稱之為Zero-padding。除了,能夠保留更多有效資訊之外,padding操作還可以保證在使用卷積計算前後卷的高和寬不變化。
padding操作需要使用到numpy中的一個函式:np.pad()。假設我們要填充一個數組a,維度為(5,5,5,5,5),如果我們想要第二個維度的pad=1,第4個維度的pad=3,其餘pad=0,那麼我們如下使用np.pad()
a = np.pad(a, ((0,0),(1,1),(0,0),(3,3),(0,0)), 'constant', constant_values = (...,...))def zero_pad(X, pad):
X_pad = np.pad(X, ((0,0),(pad,pad),(pad,pad),(0,0)), 'constant')
return X_padx = np.random.randn(4,3,3,2)
x_pad = zero_pad(x, 2)
print('x.shape=',x.shape)
print('x_pad.shape=',x_pad.shape)
print('x[1,1]=',x[1,1])
print('x_pad[1,1]=',x_pad[1,1])x.shape= (4, 3, 3, 2)
x_pad.shape= (4, 7, 7, 2)
x[1,1]= [[ 0.90085595 -0.68372786]
[-0.12289023 -0.93576943]
[-0.26788808 0.53035547]]
x_pad[1,1]= [[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]
[0. 0.]]fig, axarr = plt.subplots(1,2)
axarr[0].set_title('x')
axarr[0].imshow(x[0,:,:,0])
axarr[1].set_title('x_pad')
axarr[1].imshow(x_pad[0,:,:,0])
plt.show()3.2單步卷積(single step of convolution)
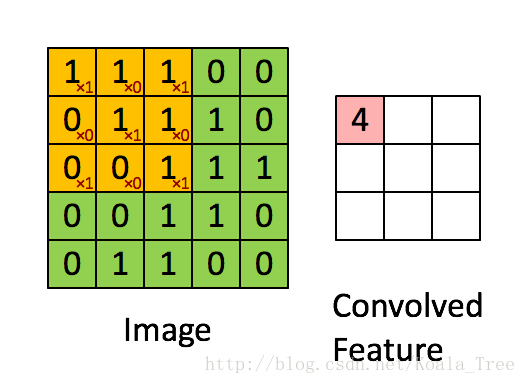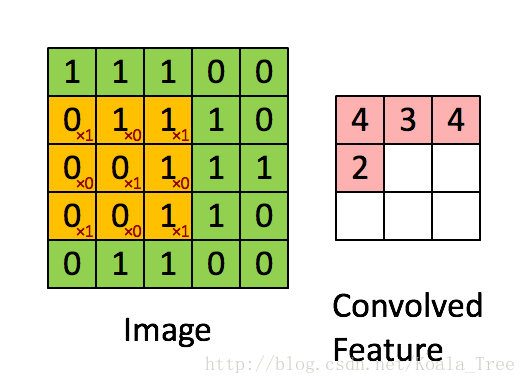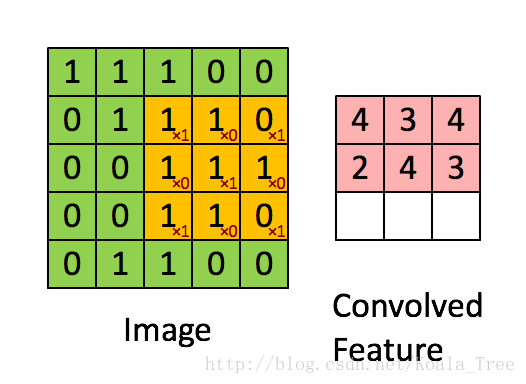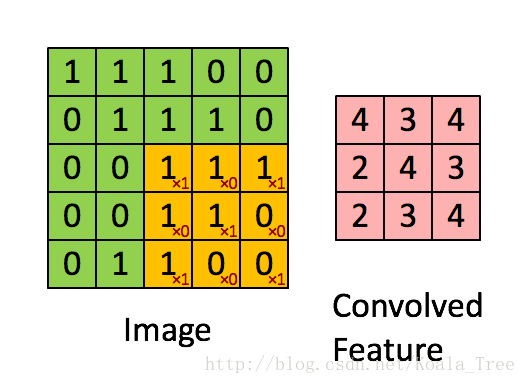
在卷積操作中,我們首先需要明確的一個概念是過濾器(核),它是一個通道數與輸入影象相同,但高度和寬度為較小奇數(通常為1,3,5,7等,我們可將這個超引數用f表示)的多維陣列(f, f, n_c)。在下面動圖示例中過濾器是(3,3)的陣列np.array([[1,0,1],[0,1,0],[1,0,1]]),其中這9個數字可以事先設定,也可以通過反向傳播來學習。設定好過濾器後還需設定步長stride(s),步長即每次移動的畫素數,在動圖示例中s=1,具體的卷積過程見下圖,最後得到一個卷積後的特徵矩陣。
def conv_single_step(a_slice_prev, W, b):
s = a_slice_prev * W
Z = np.sum(s)
Z = Z + b
return Za_slice_prev = np.random.randn(4,4,3)
W = np.random.randn(4,4,3)
b = np.random.randn(1,1,1)
Z = conv_single_step(a_slice_prev, W, b)
print('Z=',Z)Z= [[[-6.99908945]]]3.3 卷積層(convolution layer)
在3.2中給出的例子是隻有一個過濾器的情況,在CNN卷積層中過濾器會有多個,此時運算會稍微複雜但原理是一致的,只是輸出時要將每個過濾器卷積後的影象疊加在一起輸出。
在編寫程式碼前有幾個關鍵點需要說明:
1.如果想從矩陣a_prev(形狀為(5,5,3))中擷取一個(2,2)的片,我們可以
a_slice_prev = a_prev[0:2,0:2,:]2.a_slice_prev的四角vert_start, vert_end, horiz_start 和 horiz_end的定義如下圖所示。
3.卷積操作後輸出的矩陣的維度滿足以下三個公式:
def conv_forward(A_prev, W, b, hparameters):
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(f, f, n_C_prev, n_C) = W.shape
stride = hparameters['stride']
pad = hparameters['pad']
n_H = int((n_H_prev - f + 2*pad) / stride + 1)
n_W = int((n_W_prev - f + 2*pad) / stride + 1)
Z = np.zeros((m, n_H, n_W, n_C))
A_prev_pad = zero_pad(A_prev, pad)
for i in range(m):
a_prev_pad = A_prev_pad[i, :, :, :]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = stride * h
vert_end = vert_start + f
horiz_start = stride * w
horiz_end = horiz_start + f
a_slice_prev = a_prev_pad[vert_start:vert_end,
horiz_start:horiz_end,:]
Z[i, h, w, c] = conv_single_step(a_slice_prev, W[:,:,:,c],
b[:,:,:,c])
assert(Z.shape == (m, n_H, n_W, n_C))
cache = (A_prev, W, b, hparameters)
return Z, cacheA_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
"stride": 2}
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
print("Z's mean=", np.mean(Z))
print("Z[3,2,1]=",Z[3,2,1])
print("cache_conv[0][1][2][3]=",cache_conv[0][1][2][3])Z's mean= 0.048995203528855794
Z[3,2,1]= [-0.61490741 -6.7439236 -2.55153897 1.75698377 3.56208902 0.53036437
5.18531798 8.75898442]
cache_conv[0][1][2][3]= [-0.20075807 0.18656139 0.41005165]3.4池化層(pooling layer)
池化層的作用是縮減網路的大小,提高計算速度,同時可提高所提取特徵的魯棒性,主要兩種型別:最大池化(max-pooling)和平均池化(average-pooling)。
池化層沒有需要使用反向傳播進行學習的引數,但是有兩個超引數需要考慮:視窗大小(f)和步長(s)
池化後輸出的矩陣的維度滿足以下三個公式:
def pool_forward(A_prev, hparameters, mode = "max"):
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
f = hparameters["f"]
stride = hparameters["stride"]
n_H = int(1 + (n_H_prev - f) / stride)
n_W = int(1 + (n_W_prev - f) / stride)
n_C = n_C_prev
A = np.zeros((m, n_H, n_W, n_C))
for i in range(m):
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start +f
a_prev_slice = A_prev[i, vert_start:vert_end,
horiz_start:horiz_end,c]
if mode == "max":
A[i,h,w,c] = np.max(a_prev_slice)
elif mode == "average":
A[i,h,w,c] = np.mean(a_prev_slice)
assert(A.shape == (m, n_H, n_W, n_C))
cache = (A_prev, hparameters)
return A, cacheA_prev = np.random.randn(2,4,4,3)
hparameters = {"stride":2, "f":3}
A,cache = pool_forward(A_prev, hparameters)
print("mode = max")
print("A=",A)
print()
A,cache = pool_forward(A_prev, hparameters, mode="average")
print("mode = average")
print("A=",A)mode = max
A= [[[[1.74481176 0.86540763 1.13376944]]]
[[[1.13162939 1.51981682 2.18557541]]]]
mode = average
A= [[[[ 0.02105773 -0.20328806 -0.40389855]]]
[[[-0.22154621 0.51716526 0.48155844]]]]4.反向傳播過程
在使用深度學習框架情況下,我們只要保證前向傳播的過程即可,框架會自動執行反向傳播的過程,因此深度學習工程師不需要關注反向傳播的過程。CNN的反向傳播過程相對複雜,但是瞭解其實現的過程可幫助我們更好的瞭解整個模型,當然如果沒時間可以跳過本節直接進入到使用TensorFlow構建CNN。
4.1卷積層的反向傳播
4.1.1計算dA
假設過濾器的引數矩陣為Wc,則dA的計算公式如下圖:
其中dZhw是卷積層輸出Z的第h行w列的梯度下降值,在更新dA時每次用不同的dZ與Wc想乘,這主要是因為在前向傳播時,每個過濾器都是和矩陣a_prev的切片點乘後求和,因此在計算dA的反向傳播時要加上所有切片對應的梯度值。我們可以將這個公式寫成:
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] += W[:,:,:,c] * dZ[i,h,w,c]4.1.2計算dW
dWc的計算公式為
其中a_slice為計算Zij時從a_prev擷取的計算矩陣,該式可寫為:
dW[:,:,:,c] += a_slice * dZ[i, h, w, c]4.1.3計算db
db的計算公式為:
可見db為dZ的和,該式可寫為:
db[:,:,:,c] += dZ[i, h, w, c]def conv_backward(dZ, cache):
(A_prev, W, b, hparameters) = cache
(m, n_H_prev, n_W_prev, n_C_prev) = A_prev.shape
(f, f, n_C_prev, n_C) = W.shape
stride = hparameters['stride']
pad = hparameters['pad']
(m, n_H, n_W, n_C) = dZ.shape
dA_prev = np.zeros((m, n_H_prev, n_W_prev, n_C_prev))
dW = np.zeros((f, f, n_C_prev, n_C))
db = np.zeros((1,1,1,n_C))
A_prev_pad = zero_pad(A_prev, pad)
dA_prev_pad = zero_pad(dA_prev, pad)
for i in range(m):
a_prev_pad = A_prev_pad[i, :, :, :]
da_prev_pad = dA_prev_pad[i, :, :, :]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = h * stride
vert_end = vert_start + f
horiz_start = w * stride
horiz_end = horiz_start + f
a_slice = a_prev_pad[vert_start:vert_end,
horiz_start:horiz_end, :]
da_prev_pad[vert_start:vert_end, horiz_start:horiz_end, :] \
+= W[:,:,:,c] * dZ[i,h,w,c]
dW[:,:,:,c] += a_slice * dZ[i,h,w,c]
db[:,:,:,c] += dZ[i,h,w,c]
dA_prev[i,:,:,:] = da_prev_pad[pad:-pad, pad:-pad,:]
assert(dA_prev.shape == (m, n_H_prev, n_W_prev, n_C_prev))
return dA_prev, dW, dbA_prev = np.random.randn(10,4,4,3)
W = np.random.randn(2,2,3,8)
b = np.random.randn(1,1,1,8)
hparameters = {"pad" : 2,
"stride": 2}
Z, cache_conv = conv_forward(A_prev, W, b, hparameters)
dA, dW, db = conv_backward(Z, cache_conv)
print("dA_mean =", np.mean(dA))
print("dW_mean =", np.mean(dW))
print("db_mean =", np.mean(db))
dA_mean = 1.4524377775388075
dW_mean = 1.7269914583139097
db_mean = 7.8392325646168384.2池化層的反向傳播
雖然在pooling層沒有需要使用反向傳播來更新的引數,但其前有卷積層因此還是需要做反向傳播運算。
4.2.1max-pooling的反向傳播
首先我們先建立一個輔助函式creat_mask_from_window(),這個函式的主要作用是將Window矩陣中最大的元素標誌為1,其餘為0.
def create_mask_from_window(x):
mask = (x == np.max(x))
return mask其中mask = (x == np.max(x)),判斷的過程如下:
A[i,j] = True if X[i,j] == x
A[i,j] = False if X[i,j] != x測試create_mask_from_window函式
x = np.random.randn(2,3)
mask = create_mask_from_window(x)
print('x = ', x)
print("mask = ", mask)x = [[ 1.62434536 -0.61175641 -0.52817175]
[-1.07296862 0.86540763 -2.3015387 ]]
mask = [[ True False False]
[False False False]]我們之所以要追蹤最大元素的位置,是因為在池化過程中該元素對輸出起到了決定性作用,而且會影響到cost的計算。
4.2.2Average pooling的反向傳播
與max-pooling輸出只受最大值影響不同,average pooling中視窗輸入元素之間的同等重要,因此在反向傳播中也要給予各元素相同的權重。假設在前向傳播中使用的2x2過濾器,因此在反向傳播中mask矩陣將如下運算:
def distribute_value(dz, shape):
(n_H, n_W) = shape
average = dz / (n_H * n_W)
a = average * np.ones(shape)
return aa = distribute_value(2, (2,2))
print('distributed value =', a)distributed value = [[0.5 0.5]
[0.5 0.5]]4.2.3 整合pooling反向傳播
def pool_backward(dA, cache, mode="max"):
(A_prev, hparameters) = cache
stride = hparameters['stride']
f = hparameters['f']
m, n_H_prev, n_W_prev, n_C_prev = A_prev.shape
m, n_H, n_W, n_C = dA.shape
dA_prev = np.zeros(np.shape(A_prev))
for i in range(m):
a_prev = A_prev[i,:,:,:]
for h in range(n_H):
for w in range(n_W):
for c in range(n_C):
vert_start = stride * h
vert_end = vert_start + f
horiz_start = stride * w
horiz_end = horiz_start + f
if mode == "max":
a_prev_slice = a_prev[vert_start:vert_end,
horiz_start:horiz_end,c]
mask = create_mask_from_window(a_prev_slice)
dA_prev[i, vert_start:vert_end,horiz_start:horiz_end,c]\
+= np.multiply(mask, dA[i,h,w,c])
elif mode == "average":
da = dA[i, h, w, c]
shape = (f, f)
dA_prev[i, vert_start:vert_end,horiz_start:horiz_end,c]\
+= distribute_value(da, shape)
assert(dA_prev.shape == A_prev.shape)
return dA_prevA_prev = np.random.randn(5, 5, 3, 2)
hparameters = {"stride" : 1, "f": 2}
A, cache = pool_forward(A_prev, hparameters)
dA = np.random.randn(5, 4, 2, 2)
dA_prev = pool_backward(dA, cache, mode = "max")
print("mode = max")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1])
print()
dA_prev = pool_backward(dA, cache, mode = "average")
print("mode = average")
print('mean of dA = ', np.mean(dA))
print('dA_prev[1,1] = ', dA_prev[1,1]) mode = max
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0. 0. ]
[ 5.05844394 -1.68282702]
[ 0. 0. ]]
mode = average
mean of dA = 0.14571390272918056
dA_prev[1,1] = [[ 0.08485462 0.2787552 ]
[ 1.26461098 -0.25749373]
[ 1.17975636 -0.53624893]]至此,我們瞭解CNN中卷積層和池化層的構造以及前向傳播和反向傳播的過程,下面我們將使用TensorFlow框架來搭建CNN,並用以識別數字手勢圖形。
5.卷積神經網路的應用
在前面小節中我們使用python來構建函式逐步瞭解CNN的機制,而大多數深度學習的實際應用中都是使用某一個深度學習框架來完成的, 下面我們將會看到使用深度學習框架的內建函式帶來的便利。
這是我們要用到的第三方庫和輔助程式,涉及到的資料和程式碼可從這裡下載。
import math
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
import tensorflow as tf
from tensorflow.python.framework import ops
from cnn_utils import *
np.random.seed(1)執行下列程式碼,匯入給定的資料集。
X_train_orig, Y_train_orig, X_test_orit, Y_test_orig, classes = load_dataset()def load_dataset():
train_dataset = h5py.File('datasets\\train_signs.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # your train set features
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # your train set labels
test_dataset = h5py.File('datasets\\test_signs.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # your test set features
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # your test set labels
classes = np.array(test_dataset["list_classes"][:]) # the list of classes
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classes資料集是0-6六個資料的手勢圖片,如下:
我們隨意選取資料集中的一個樣本顯示。
index = 0
plt.imshow(X_train_orig[index])
plt.show()
print("y=" + str(np.squeeze(Y_train_orig[:,index])))輸出標籤為
y= 5在之前的文章裡已經介紹過資料處理的相關內容,可參見文章《使用TensorFlow搭建深層神經網路》。
X_train = X_train_orig / 255
X_test = X_test_orig / 255
Y_train = convert_to_one_hot(Y_train_orig, 6).T
Y_test = convert_to_one_hot(Y_test_orig, 6).T
print ("number of training examples = " + str(X_train.shape[0]))
print ("number of test examples = " + str(X_test.shape[0]))
print ("X_train shape: " + str(X_train.shape))
print ("Y_train shape: " + str(Y_train.shape))
print ("X_test shape: " + str(X_test.shape))
print ("Y_test shape: " + str(Y_test.shape))
conv_layers = {}
number of training examples = 1080
number of test examples = 120
X_train shape: (1080, 64, 64, 3)
Y_train shape: (1080, 6)
X_test shape: (120, 64, 64, 3)
Y_test shape: (120, 6)5.1建立placeholders
我們知道在TensorFlow框架下,在執行Session時想要給model喂資料的話,必須先建立placeholders。此時我們不用給定訓練集的樣本數,因此使用None作為batch的大小,所以X的維度是[None, n_H0, n_W0, n_C0], Y的維度是[None, n_y],程式碼如下:
def create_placeholders(n_H0, n_W0, n_C0, n_y):
X = tf.placeholder(tf.float32, shape = [None, n_H0, n_W0, n_C0])
Y = tf.placeholder(tf.float32, shape = [None, n_y])
return X, YX, Y = create_placeholders(64, 64, 3, 6)
print ("X = " + str(X))
print ("Y = " + str(Y))X = Tensor("Placeholder:0", shape=(?, 64, 64, 3), dtype=float32)
Y = Tensor("Placeholder_1:0", shape=(?, 6), dtype=float32)5.2初始化引數
假設我們要初始一個引數,其shape為[1,2,3,4],在TensorFlow中初始方式如下:
W = tf.get_variable('W', [1, 2, 3, 4], initializer = ...)我們只需要初始化權重或過濾器的引數W1,W2即可, 而偏差b、全連線層的引數學習框架會自動幫我們處理,不用在意。
def initialize_parameters():
tf.set_random_seed(1)
W1 = tf.get_variable("W1", [4, 4, 3, 8], initializer=tf.contrib.layers.xavier_initializer(seed=0))
W2 = tf.get_variable("W2", [2, 2, 8, 16], initializer=tf.contrib.layers.xavier_initializer(seed=0))
parameters = {"W1" : W1,
"W2" : W2}
return parameterstf.reset_default_graph()
with tf.Session() as sess:
parameters = initialize_parameters()
init = tf.global_variables_initializer()
sess.run(init)
print("W1 = " + str(parameters["W1"].eval()[1,1,1]))
print("W2 = " + str(parameters["W2"].eval()[1,1,1]))W1 = [ 0.00131723 0.1417614 -0.04434952 0.09197326 0.14984085 -0.03514394
-0.06847463 0.05245192]
W2 = [-0.08566415 0.17750949 0.11974221 0.16773748 -0.0830943 -0.08058
-0.00577033 -0.14643836 0.24162132 -0.05857408 -0.19055021 0.1345228
-0.22779644 -0.1601823 -0.16117483 -0.10286498]5.3前向傳播
正如多次提及的,使用深度學習框架我們只要處理好前向傳播過程,框架會自動幫助我們處理反向傳播的過程;而在框架中內建了很多函式可以為我們執行卷積步驟,比如:
(1)tf.nn.conv2d(X, W1, strides = [1, s, s, 1], padding = 'SAME'):這個函式將輸入X和W1進行卷積計算,第三個輸入strides 規定了在X(shape為(m, n_H_prev, n_W_prev, n_C_prev))各維度上的步長s,第四個輸入padding規定padding的方式;
(2)tf.nn.max_pool(A, ksize = [1, f, f, 1], strides = [1, s, s, 1], padding = 'SAME'):這個函式是以ksize和strides規定的方式對輸入A進行max-pooling操作;
(3)tf.nn.relu(Z1):Relu作為啟用函式;
(4)tf.contrib.layers.flatten(P):將P中每個樣本flatten成一維向量,最後返回一個flatten的shape為[batch_size, k]的圖;
(5)tf.contrib.layers.fully_connected(F, num_outputs):給定flatten的輸入F, 返回一個經全連線層計算的值num_outputs。使用此函式時,可以自動的初始化全連線層的權重系統並且在訓練網路時訓練權重。
本程式中我們的前向傳播過程包括如下步驟: CONV2D - > RELU -> MAXPOOL -> CONV2D -> RELU -> MAXPOOL -> FLATTEN -> FULLCONNECTED,各步驟中使用的引數如下:
CONV2D - > stride = 1, padding = "SAME"
RELU ->
MAXPOOL -> f = 8, stride = 8, padding = "SAME"
CONV2D -> stride = 1, padding = "SAME"
RELU ->
MAXPOOL -> f = 4, stride = 4, padding = "SAME"
FLATTEN ->
FULLCONNECTED:不需要呼叫softmax,因為在這裡FC層會輸出6個神經元之後會傳遞給softmax,而在TensorFlow中softmax和cost結成在另外一個單獨的函式中。
def forward_propagation(X, parameters):
W1 = parameters['W1'] / np.sqrt(2)
W2 = parameters['W2'] / np.sqrt(2)
Z1 = tf.nn.conv2d(X, W1, strides=[1,1,1,1], padding='SAME')
A1 = tf.nn.relu(Z1)
P1 = tf.nn.max_pool(A1, ksize=[1,8,8,1], strides=[1,8,8,1], padding='SAME')
Z2 = tf.nn.conv2d(P1, W2, strides=[1,1,1,1], padding='SAME')
A2 = tf.nn.relu(Z2)
P2 = tf.nn.max_pool(A2, ksize=[1,4,4,1], strides=[1,4,4,1], padding='SAME')
P2 = tf.contrib.layers.flatten(P2)
Z3 = tf.contrib.layers.fully_connected(P2, 6, activation_fn=None)
return Z3tips:在初始化W1,W2時我們使用的初始化tf.contrib.layers.xavier_initializer,這裡xavier只使用np.sqrt(1/n),然而對於relu啟用函式使用np.sqrt(1/n)可以取得更好的效果,因此我們需要在初始化後再使用W1,W2時需要再除以np.sqrt(2)。
tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(Z3, {X:np.random.randn(2,64,64,3), Y:np.random.randn(2,6)})
print('Z3 = ' + str(a))Z3 = [[ 1.4416984 -0.24909666 5.450499 -0.2618962 -0.20669907 1.3654671 ]
[ 1.4070846 -0.02573211 5.08928 -0.48669922 -0.40940708 1.2624859 ]]5.4計算cost
在計算cost時我們需要用到如下兩個內建函式:
(1)tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y):這個函式在計算softmax啟用函式同時可計算loss結果;
(2)tf.reduce_mean:這個函式對所有的loss求和得到cost值。
def compute_cost(Z3, Y):
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = Z3, labels = Y))
return costtf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
print("cost = " + str(a))tf.reset_default_graph()
with tf.Session() as sess:
np.random.seed(1)
X, Y = create_placeholders(64, 64, 3, 6)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
init = tf.global_variables_initializer()
sess.run(init)
a = sess.run(cost, {X: np.random.randn(4,64,64,3), Y: np.random.randn(4,6)})
print("cost = " + str(a))Z3 = [[ 0.63031745 -0.9877705 -0.4421346 0.05680432 0.5849418 0.12013616]
[ 0.43707377 -1.0388098 -0.5433439 0.0261174 0.57343066 0.02666192]]tips:此處跟達叔課後答案有些不同,是因為我們使用的TensorFlow版本不同而已。
5.5整合model
整個model分如下幾部:
(1)建立placeholders
(2)初始化引數
(3)前向傳播
(4)計算cost
(5)建立optimizer
(6)執行Session
def model(X_train, Y_train, X_test, Y_test, learning_rate=0.009,
num_epochs = 100, minibatch_size = 64, print_cost = True):
ops.reset_default_graph()
tf.set_random_seed(1)
seed = 3
(m, n_H0, n_W0, n_C0) = X_train.shape
n_y = Y_train.shape[1]
costs = []
X, Y = create_placeholders(n_H0, n_W0, n_C0, n_y)
parameters = initialize_parameters()
Z3 = forward_propagation(X, parameters)
cost = compute_cost(Z3, Y)
optimizer = tf.train.AdamOptimizer(learning_rate).minimize(cost)
init = tf.global_variables_initializer()
with tf.Session() as sess:
sess.run(init)
for epoch in range(num_epochs):
minibatch_cost = 0
num_minibatches = int(m / minibatch_size)
seed = seed + 1
minibatches = random_mini_batches(X_train, Y_train, minibatch_size, seed)
for minibatch in minibatches:
(minibatch_X, minibatch_Y) = minibatch
_ , temp_cost = sess.run([optimizer, cost], feed_dict={X:minibatch_X, Y:minibatch_Y})
minibatch_cost += temp_cost / num_minibatches
if print_cost == True and epoch % 10 == 0:
print("Cost after epoch %i:%f"%(epoch, minibatch_cost))
if print_cost == True and epoch % 1 == 0:
costs.append(minibatch_cost)
plt.plot(np.squeeze(costs))
plt.ylabel('cost')
plt.xlabel('iterations (per tens)')
plt.title('learning rate =' + str(learning_rate))
plt.show()
predict_op = tf.argmax(Z3, 1)
correct_prediction = tf.equal(predict_op, tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float"))
print(accuracy)
train_accuracy = accuracy.eval({X:X_train, Y:Y_train})
test_accuracy = accuracy.eval({X:X_test, Y:Y_test})
print("Train Accuracy:", train_accuracy)
print("Test Accuracy:", test_accuracy)
return train_accuracy, test_accuracy, parameters_, _, parameters = model(X_train, Y_train, X_test, Y_test)Cost after epoch 0:1.906084
Cost after epoch 10:0.971529
Cost after epoch 20:0.648505
Cost after epoch 30:0.463869
Cost after epoch 40:0.385492
Cost after epoch 50:0.327990
Cost after epoch 60:0.266418
Cost after epoch 70:0.224210
Cost after epoch 80:0.248607
Cost after epoch 90:0.158102Train Accuracy: 0.94166666
Test Accuracy: 0.825在此我們設定num_epochs = 100,可以通過增加迭代代數來提高精度,比如500代。
fname = "images\\myfigure.jpg"
image = np.array(ndimage.imread(fname, flatten=False))
my_image = scipy.misc.imresize(image, size=(64,64))
plt.imshow(image)
plt.show()