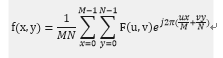前段時間看了很多的概念和知識，發現因為是走馬觀花的過了一遍，所以看得稀裡糊塗的，然後許多地方混淆了概念，特別是關於影象頻率域的部分的理解（包括影象頻率域濾波之類的），所以下面總結一下這段時間重新看《數字影象處理》（電子工業出版社，Matlab本科教學版）第三章重新收穫的關於頻率域的理解。

首先，我們要明確的概念是空間域和頻率域，我們通過imread函式得到的一幅影象(基本上也是我們平時說的影象)，是處在空間域的，也就是說用f(x,y)表徵的某一點的灰度值（或者是單色影象中某一點的亮度）的這種形式，就是在空間域裡面。

那麼什麼是影象的頻率域呢？理解了影象的頻率的概念，就不難理解頻率域。我個人理解是這麼類比的，影象可以看成是一個特殊的二維的訊號，然後某一點的灰度級，其實就是影象訊號上這一點的”幅度“，那麼根據訊號的概念，頻率就是訊號變化的快慢，這樣就好理解了，所謂的頻率也就是這個圖空間上的灰度變換的快慢，或者是叫影象的梯度變化，什麼地方梯度頻率比較大呢？這在影象中自然是“邊界”比較大。舉個例子來講，如果一幅圖整體變化不大（比如說是一面牆的圖），那麼他在頻率域下低頻成分就很多，而高頻成分就極少。而顯然如果是一幅國際象棋棋盤，他的高頻成分相對剛才那幅牆的圖片來說，肯定多得多。

然後從影象域變換到頻率域，我們用的函式就是大名鼎鼎的二維離散傅立葉變換了:

令f(x,y)表示一幅大小為MXN畫素的數字影象，其中，x=0，1，2······M-1, y=0，1，2······N-1，由F(u，v)表示的f(x，y)的二維離散傅立葉變換（DFT）由下式給出：

式子當中，u也是屬於0到M-1,v屬於0到N-1。頻率域就是屬於u，v作為頻率變數，由F(u，v)構成的座標系，這塊MXN的區域我們通常稱為頻率矩形，很明顯頻率矩形的大小和輸入影象的大小相同。

有傅立葉變換，當然就有傅立葉反變換(IDFT)：

這裡多提一句，按照書上的說法，在DFT的表示式中，1/MN項出現在正變換前面，而在有些表示式中就如上式那樣出現在反變換前面，因為Matlab採用的是後者，所以書上的公式就是用的上式那種了。

由上面的公式可以看出幾個點：

1.    不難看出，F(0，0)等於f(x,y)平均值的MN倍,因為帶入到傅立葉變換公式中可以得到F(0，0)實際上就是影象中所有f(x，y)求和。所以我們也常把F(0，0)稱作傅立葉變換的直流分量。

2.    我們可以很明顯的看出，在頻率域中的一點(u,v)的值F(u，v)，他並不決定於空間域中（x,y）的值，而是跟整個影象空間域中的所有的點都有關係，因此，在頻率域中的一點(u,v)的值，例如說F(5,5)和空間域上的這一點f(5,5)並沒有什麼關係，而是決定於整幅影象。

接下來書上講了傅立葉變換的一些性質，還有傅立葉譜，變換的相角定義，功率譜定義等等概念，因為打公式太麻煩，這裡就不多贅述了，可以在網上找到現成的公式定義和概念。

    傅立葉變換性質裡面個人認為比較重要的是週期性，因為週期性的緣故，所以在傅立葉變換過後的頻率圖裡，四角的是低頻分量（具體的我也不太清楚，但是比如低頻分量），我們到時候會把低頻分量移到中心位置來，因為大部分影象的低頻分量其實更多，所以會在邊角上比較亮，放到中間來比較好看。

    下面舉例一幅圖說明看一幅頻率域傅立葉譜圖:

1. f=imread('3.jpg');

2. imshow(f);%顯示原圖

3. F=fft2(f);%做傅立葉變換

4. S=abs(F);%取傅立葉譜

5. figure,imshow(S,[]);%顯示傅立葉譜

左圖是原圖，右圖是頻率圖，頻率圖中的亮暗說明了對應頻率的多少，上面已經談過，如果從右圖可以看出來是邊上的四個點比較亮，這說明原圖中低頻分量比較多，也就是說原圖中的變化比較少。換句話來說，如果原圖看成地形的話，那說明大部分地形非常平坦。

我們可以通過公式（尤拉公式e^(2*pi*j)=1以及指數的計算），可以很容易發現（圖是盜的- -）：

上式最左邊那個符號表示求傅立葉變換。由上式知道這麼弄一番之後，是可以把頻率圖的原點放到中心的。

在matlab中用的是fftshift函式。

居中過後的頻率譜顯示如下：

可以看得更清楚一些，這個時候因為其實頻率譜的範圍是很大的，相對於低頻分量來說，高頻分量的值比較少，所以可以用對數變換(log(1+abs(F))將高頻細節擴展出來，顯示如下：

細節還是突出的比較明顯的哈！

下面談談對濾波的理解，不知道是不是完全正確。

濾波和運算元都是數字影象處理的基本操作，其中濾波是指在畫素領域（空間域）內做領域處理(中值濾波、均值濾波)或者在影象頻域內（需要先做傅立葉變換）做處理（低通濾波、高通濾波、帶通濾波）。運算元一般就是指的是卷積運算元了。

先來談談空間域的濾波。什麼叫領域處理呢？領域處理的就是對領域進行一系列的操作：

(1)    選取中心點(x,y)；

(2)    僅對預先定義的點（x,y）的領域內的畫素執行操作;

(3)    令運算結果為該點處的響應；

(4)    對影象中的每一點重複該處理。

中心點移動的過程中會產生新的領域，每個領域對應輸入影象上的一個畫素。用來標識該處理的兩個主要術語是領域處理和空間濾波，其中後者更為通用。如果對領域中畫素執行的計算是線性的，則稱該操作是線性空間濾波。（也用術語空間卷積）；否則稱為非線性空間濾波。

線性操作包括領域中的每個畫素乘以相應的係數，將結果求和，從而得到點(x,y)處的響應。若領域的大小為mxn，則需要mn個係數。這些係數被排列為一個矩陣，稱為濾波器(模板)/濾波模板/核/掩模或者視窗。其中前三個屬於最常見。為變得更明顯一些，也用卷積濾波、卷積模板或者卷積核等術語。

再來說下卷積運算元是個什麼意思：

在這裡盜一下網上的圖：

然後如上所示，圖片中右上角的那個矩陣h=[2 9 4;

                                        7 5 3;

                                        6 1 8;]

就是後面經常提到的模板了，在相關書本上一般也寫作w(x,y)。如果把基於乘積和的值用來替代成原來的(x,y)的值，那麼這種濾波方式叫做線性濾波（比如拉普拉斯運算元）。其他的叫做非線性濾波。

空間域濾波的最常見的就是中值濾波和均值濾波，顧名思義，中值濾波就是用影象領域中所包含的畫素的排序集合的中值進行替代，而均值濾波是用領域畫素們的均值進行濾波。中值濾波也屬於統計排序濾波。

接下來介紹頻率域的濾波：

首先，有個定理，叫做卷積定理：

   f(x,y)★h(x,y)óH(u,v)F(u,v)

上式中★代表卷積，ó代表一個傅立葉變換對。

頻率域的濾波比較多的就是高斯低通/高斯高通濾波器了，和空間域稍微有區別的是，在頻率域內不是進行的領域處理，而是進行的是函式修改：

G(u，v)= H(u,v)F(u,v)

函式H(u,v)又叫做濾波器傳遞函式，頻率域濾波的思想就是選擇一個濾波器傳遞函式，該函式按照指定的方式修改F(u，v)。

由卷積定理可知，在頻率域中讓F(u,v)乘以空間濾波器的傅立葉變換H(u，v)，再做一個傅立葉反變換，就可以得到用空間域濾波器濾波後的影象了（這也是相當於用DFT的方式在做卷積，用這種方式做卷積又叫迴圈卷積）。

值得一提的是，注意，當作迴圈卷積的時候，因為F和H都是周期函式，所以G必然也是周期函式，在週期接近函式非零部分的持續週期時對周期函式進行卷積會引起相鄰週期的串擾(這種串擾又叫摺疊誤差)，所以要通過補零的方法來避免。比較拗口，還是舉例來說明：一個上黑下白的方塊圖片，在DFT卷積的時候我們假設在處理上邊沿了，結果因為是週期的所以上邊沿其實在處理時會受到上邊沿上面另一個方塊的下邊沿的白色部分的影響（具體的例子見書P63頁），補0之後就不會受影響了。