【圖形影象】幾何不變矩---Hu矩
阿新 • • 發佈:2019-01-25
在連續情況下,影象函式為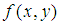 ,那麼影象的p+q階幾何矩(標準矩)定義為:
,那麼影象的p+q階幾何矩(標準矩)定義為:
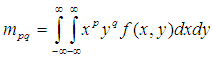
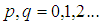
p+q階中心距定義為:
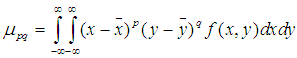
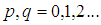
其中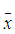 和
和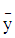 代表影象的重心,
代表影象的重心,
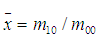
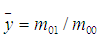
對於離散的數字影象,採用求和號代替積分:
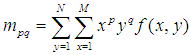
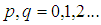
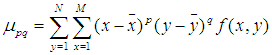
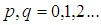
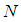 和
和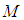 分別是影象的高度和寬度;
分別是影象的高度和寬度;
歸一化的中心距定義為:
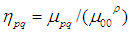 ;其中
;其中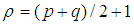
利用二階和三階歸一化中心矩構造了7個不變矩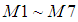 :
:
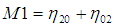
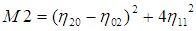
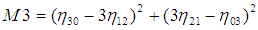
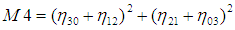
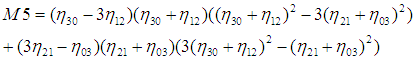
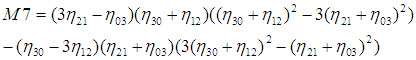
這7個不變矩構成一組特徵量,Hu.M.K在1962年證明了他們具有旋轉,縮放和平移不變性。
實際上,在對圖片中物體的識別過程中,只有 和
和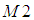 不變性保持的比較好,其他的幾個不變矩帶來的誤差比較大,有學者認為只有基於二階矩的不變矩對二維物體的描述才是真正的具有旋轉、縮放和平移不變性(
不變性保持的比較好,其他的幾個不變矩帶來的誤差比較大,有學者認為只有基於二階矩的不變矩對二維物體的描述才是真正的具有旋轉、縮放和平移不變性(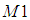
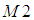 剛好都是由二階矩組成的)。不過我沒有證明是否是真的事這樣的。
剛好都是由二階矩組成的)。不過我沒有證明是否是真的事這樣的。
由Hu矩組成的特徵量對圖片進行識別,優點就是速度很快,缺點是識別率比較低,我做過手勢識別,對於已經分割好的手勢輪廓圖,識別率也就30%左右,對於紋理比較豐富的圖片,識別率更是不堪入眼,只有10%左右。這一部分原因是由於Hu不變矩只用到低階矩(最多也就用到三階矩),對於影象的細節未能很好的描述出來,導致對影象的描述不夠完整。
Hu不變矩一般用來識別影象中大的物體,對於物體的形狀描述得比較好,影象的紋理特徵不能太複雜,像識別水果的形狀,或者對於車牌中的簡單字元的識別效果會相對好一些。
C++程式碼:
- // 影象位數對齊
-
#define bpl(imwidth, deep) ((imwidth*deep*8+31)/32*4)
- /* 獲取畫素值
- psrcBmp: 影象資料指標
- nsrcBmpWidth: 影象寬度,以畫素為單位
- x,y: 畫素點
- deep: 影象的位數深度,(表示位的灰度圖,表示位的 RGB 點陣圖)
- */
- COLORREF J_getpixel( constBYTE *psrcBmp, constint nsrcBmpWidth, constint x, constint y, int deep = 3)
- {
- if (deep == 3)
- {
-
return RGB(*(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) + 2 ) ,
- *(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) + 1 ) ,
- *(psrcBmp + x*3 + y*bpl(nsrcBmpWidth, deep) +0 ));
- }
- elseif (deep == 1)
- {
- return *(psrcBmp + x + y*bpl(nsrcBmpWidth, deep));
- }
- }
- // 獲取標準矩 ( 只支援位灰度圖 )
- void GetStdMoment (BYTE *psrcBmp ,
- int nsrcBmpWidth ,
- int nsrcBmpHeight ,
- double *m )
- {
- for ( int p = 0 ; p < 2 ; p ++ )
- for ( int q = 0 ; q < 2 ; q ++ )
- {
- if ( p == 1 && q == 1)
- break ;
- for ( int y = 0 ; y < nsrcBmpHeight ; y ++ )
- for ( int x = 0 ; x < nsrcBmpWidth ; x ++ )
- m [p *2+q ] += (pow ( (double )x , p ) * pow ( (double )y , q ) * J_getpixel (psrcBmp , nsrcBmpWidth , x ,y , 1));
- }
- }
- //hu 不變矩 ( 只支援位灰度圖 )
- void J_GetHuMoment (BYTE *psrcBmp ,
- int nsrcBmpWidth ,
- int nsrcBmpHeight ,
- double *H )
- {
- double m [4] = {0.0};
- GetStdMoment (psrcBmp ,
- nsrcBmpWidth ,
- nsrcBmpHeight ,
- m );
- int x0 = (int )(m [2]/m [0] + 0.5);
- int y0 = (int )(m [1]/m [0] + 0.5);
- double u [4][4] = {0.0};
- for ( int p = 0 ; p < 4 ; p ++ )
- for ( int q = 0 ; q < 4 ; q ++ )
- {
- // 優化<a href="http://lib.csdn.net/base/31" class='replace_word' title="演算法與資料結構知識庫" target='_blank' style='color:#df3434; font-weight:bold;'>演算法</a>,以下介數不用計算
- if ( (p == 0 && q == 1) ||
- (p == 1 && q == 0) ||
- (p == 1 && q == 3) ||
- (p == 2 && q == 2) ||
- (p == 2 && q == 3) ||
- (p == 3 && q == 1) ||
- (p == 3 && q == 2) ||
- (p == 3 && q == 3))
- {
- break ;
- }
- for ( int y = 0 ; y < nsrcBmpHeight ; y ++ )
- for ( int x = 0 ; x < nsrcBmpWidth ; x ++ )
- u [p ][q ] += (pow ( double (x - x0 ) , p ) * pow ( double (y - y0 ), q ) * J_getpixel (psrcBmp , nsrcBmpWidth , x , y , 1));
- }
- double n [4][4] = {0.0};
- for ( int p = 0 ; p < 4 ; p ++ )
- for ( int q = 0 ; q < 4 ; q ++ )
- {
- // 優化演算法,以下介數不用計算
- if ( (p == 0 && q == 0) ||
- (p == 0 && q == 1) ||
- (p == 1 && q == 0) ||
- (p == 1 && q == 3) ||
- (p == 2 && q == 2) ||
- (p == 2 && q == 3) ||
- (p == 3 && q == 1) ||
- (p == 3 && q == 2) ||
- (p == 3 && q == 3))
- {
- break ;
- }
- n [p ][q ] = u [p ][q ]/( pow ( u [0][0] , (p +q )/2.0 + 1 ) );
- }
- *(H ) = n [2][0] + n [0][2];
- *(H + 1) = pow (n [2][0]-n [0][2] , 2.0) + 4*pow (n [1][1],2.0);
- *(H + 2) = pow (n [3][0]-3*n [1][2] , 2) + pow (3*n [2][1] - n [0][3] , 2);
- *(H + 3) = pow (n [3][0]+n [1][2] , 2)+ pow (n [2][1]+n [0][3],2);
- *(H + 4) = (n [3][0]-3*n [1][2])*(n [3][0] + n [1][2])*(pow (n [3][0]+n [1][2],2)-3*pow (n [2][1]+n [0][3],2))+(3*n [2][1]-n [0][3])*(n [2][1]+n [0][3])*(3*pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2));
- *(H + 5) = (n [2][0]-n [0][2])*(pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2))+4*n [1][1]*(n [3][0]+n [1][2])*(n [2][1]+n [0][3]);
- *(H + 6) = (3*n [2][1]-n [0][3])*(n [3][0] + n [1][2])*(pow (n [3][0]+n [1][2],2)-3*pow (n [2][1]+n [0][3],2))+( 3*n [1][2] - n [3][0] )*(n [2][1]+n [0][3])*(3*pow (n [3][0]+n [1][2],2)-pow (n [2][1]+n [0][3],2));
- }
