目錄

卷積的特性

卷積到底是如何操作的

• 1. 對於一個特徵圖（如灰度圖）             

卷積就是對應元素乘積的求和,然後在加上一個非線性函式。

但是上面的例子只有一個輸入channel和一個卷積核，當有很多channel和多個卷積核時，又改如何計算呢？

• 2. 多個特徵圖如何和多個filter進行運算呢？

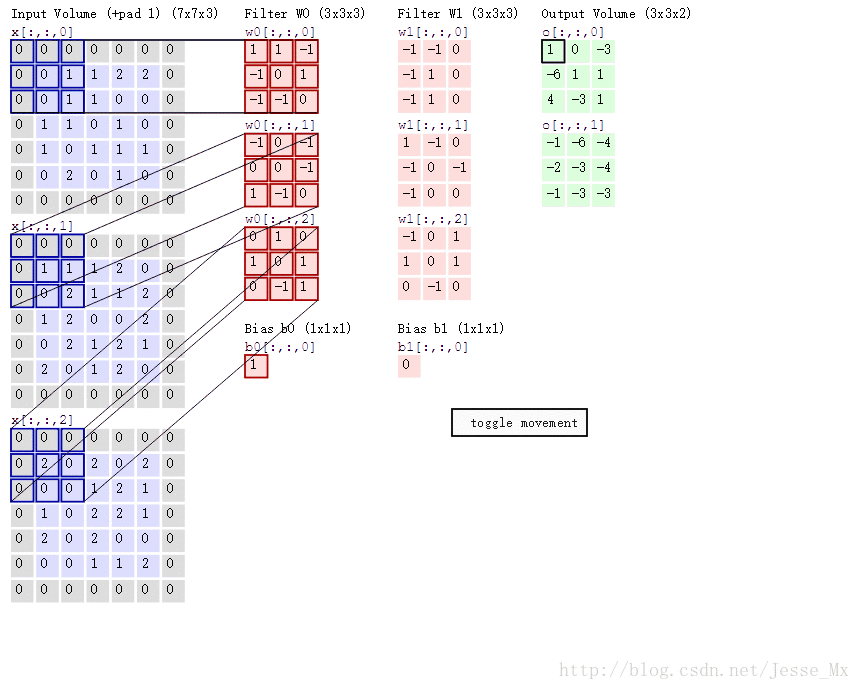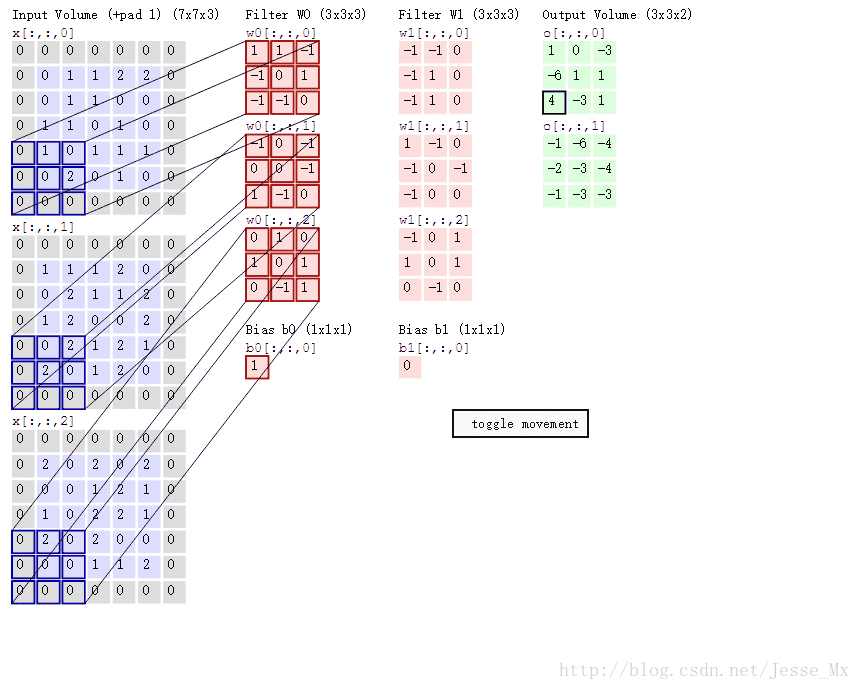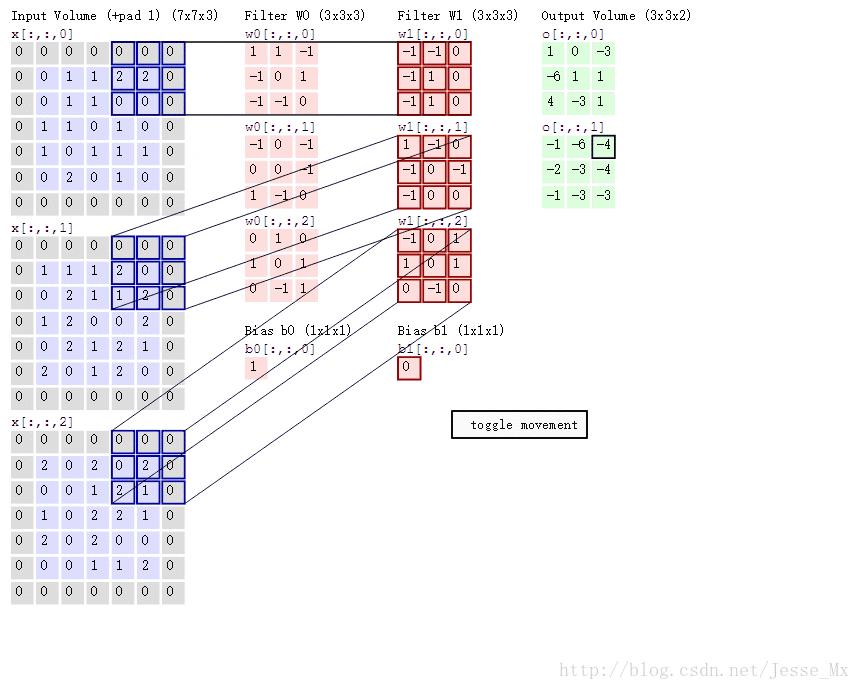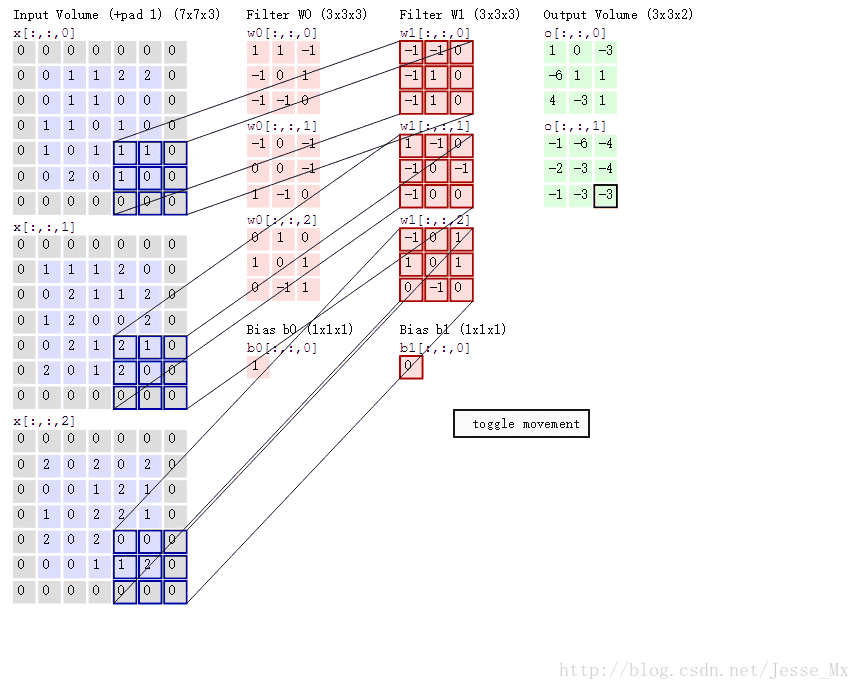
先來看動圖，這裡有三個輸入維度，兩個卷積核，最後輸出的是兩個特徵圖。

Remember：一個filter就是一個特徵，一般會有多個卷積核（也就是多個channel），所以，一個filter更多的時候是一個長方體，而不是一個平面，為什麼會這樣呢？

因為，並不是每個特徵圖和每個卷積核去匹配的，而是所有的輸入channel同時和一個filter做運算，也就是多個卷積核的對應元素乘積的求和。因此對於一個filter，它應該具有和原圖相同的channel 。如原圖是3通道的，那麼filter也應該是3通道 ​。當然filter的channel的引數不需要人為設定，因為它就是輸入層的channel數，但計算時需要考慮。

• 單個filter  -- 含有多個特徵圖（可看做彩色圖片的三個通道）

上圖看起來有三個filter，其實就是一個一個含有三個channel的filter

• 多個filter

上圖中有兩個 filter，也就是兩個特徵，每個含有三個channel，所以最後會輸出兩個特徵圖。

filter的引數如何計算

以VGG16的 block1_conv1為例，卷積核是3x3(大家肯定都知道），filter的個數是64，也就是說會輸出64個特徵圖。filter的輸入維度是3，因此引數的個數應該是    (3x3x3+1)x64 = 1792

前面3x3表示一個channel的引數數目，後面的3指的是輸入層的channel，加1表示每個filter含有偏置

再舉個例子：請看block2_conv1 它的引數應該是（3x3x64+1）x128 = 73856

In [2]:
from keras.applications.vgg16 import VGG16

In [4]:
model = VGG16()
In [5]:

model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 224, 224, 3)       0         
_________________________________________________________________
block1_conv1 (Conv2D)        (None, 224, 224, 64)      1792      
_________________________________________________________________
block1_conv2 (Conv2D)        (None, 224, 224, 64)      36928     
_________________________________________________________________
block1_pool (MaxPooling2D)   (None, 112, 112, 64)      0         
_________________________________________________________________
block2_conv1 (Conv2D)        (None, 112, 112, 128)     73856     
_________________________________________________________________
block2_conv2 (Conv2D)        (None, 112, 112, 128)     147584    
_________________________________________________________________
block2_pool (MaxPooling2D)   (None, 56, 56, 128)       0         
_________________________________________________________________
block3_conv1 (Conv2D)        (None, 56, 56, 256)       295168    
_________________________________________________________________
block3_conv2 (Conv2D)        (None, 56, 56, 256)       590080    
_________________________________________________________________
block3_conv3 (Conv2D)        (None, 56, 56, 256)       590080    
_________________________________________________________________
block3_pool (MaxPooling2D)   (None, 28, 28, 256)       0         
_________________________________________________________________
block4_conv1 (Conv2D)        (None, 28, 28, 512)       1180160   
_________________________________________________________________
block4_conv2 (Conv2D)        (None, 28, 28, 512)       2359808   
_________________________________________________________________
block4_conv3 (Conv2D)        (None, 28, 28, 512)       2359808   
_________________________________________________________________
block4_pool (MaxPooling2D)   (None, 14, 14, 512)       0         
_________________________________________________________________
block5_conv1 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_conv2 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_conv3 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_pool (MaxPooling2D)   (None, 7, 7, 512)         0         
_________________________________________________________________
flatten (Flatten)            (None, 25088)             0         
_________________________________________________________________
fc1 (Dense)                  (None, 4096)              102764544 
_________________________________________________________________
fc2 (Dense)                  (None, 4096)              16781312  
_________________________________________________________________
predictions (Dense)          (None, 1000)              4097000   
=================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
_________________________________________________________________

​
 

• 卷積的特性

• 1. 卷積的引數為甚這麼少

  • 權值共享
    因為一個特徵檢測如垂直邊緣檢測，如果適用於圖片的某個區域，一定也適用於其他區域

  • 稀疏連線
    對於每個layer,它的輸出值之和很少的輸入資料有關，如紅色圓圈的數值之和原圖中的3x3的大小的資料有關。

• 2.為啥具有平移不變性

     由於卷積的結構，即使移動幾個畫素值，仍然具有相似的特徵。

1x1的卷積核

這是最簡單的1x1卷積，這時候輸出channel是filter的channel都是1，這時候只是乘以一個倍數，顯然沒什麼作用，繼續看

現在輸出channel是32，此時才能發揮它的作用。

上文說過，filter的channel必須和輸入的channel相等，因此，這個1x1的filter 的channel也是32

操作：這個黃色的1x1的filter，先與藍色長方體的左上角的一個1x1x32的長方體，對應元素相乘，求和，然後在加一個非線性運算，如Relu,就得了右圖的一個數據點。然後依次遍歷所有的位置，就生成了一張6x6的特徵圖。

這只是一個filter，當有n的1x1的filter時，就會有n個特徵圖。

因此，有沒有發現，1x1的卷積核，並不改變影象的高寬，但可以改變模型的維度。因此也可以用於模型壓縮，繼續往後看。

• 1x1的卷積如何實現模型壓縮？

舉個栗子：我們希望實現，從28x28x192 到28x28x32的轉換

如果用5x5卷積的話，通過padding可以實現圖片尺寸不變

此時的引數個數為：（5x5x32 + 1）x 192 = 153792

但是如果，你在中間加上一層1x1的卷積，先把輸入的維度，降下來，在用5x5的卷積時，引數個數會怎麼樣呢？

引數：(1x1x16+ 1)x192 + (5x5x32 + 1)x16 = 16080，僅僅是原來的十分之一，特別當維度很高時，引數的減少越明顯。

中間的這層，也被稱為瓶頸層，bottleneck layer。

大家可能會問，把維度引數降低了這麼多，維度也從192到了16，網路結構效能不會下降嗎？

既然現在1x1的卷積被廣泛的應用，也就說明只要合理構建bottleneck layer ,既可以減少引數，運算量，也不會降低網路效能​​

1x1的卷積的典型應用，請去看inception系列的網路結構。建議去看吳恩達 Andrew Ng的網易雲課程。