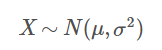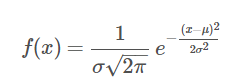基礎知識 

  二項分佈有兩個引數，一個 n 表示試驗次數，一個 p 表示一次試驗成功概率。現在考慮一列二項分佈，其中試驗次數 n 無限增加，而 p 是 n 的函式。

  1.如果 np 存在有限極限 λ，則這列二項分佈就趨於引數為 λ 的 泊松分佈。反之，如果 np 趨於無限大（如 p 是一個定值），則根據德莫佛-拉普拉斯(De'Moivre-Laplace)中心極限定理，這列二項分佈將趨近於正態分佈。

  2.實際運用中當 n 很大時一般都用正態分佈來近似計算二項分佈，但是如果同時 np 又比較小（比起 n來說很小），那麼用泊松分佈近似計算更簡單些，畢竟泊松分佈跟二項分佈一樣都是離散型分佈。

一、泊松分佈

日常生活中，大量事件是有固定頻率的。

• 某醫院平均每小時出生3個嬰兒

• 某公司平均每10分鐘接到1個電話

• 某超市平均每天銷售4包xx牌奶粉

• 某網站平均每分鐘有2次訪問

它們的特點就是，我們可以預估這些事件的總數，但是沒法知道具體的發生時間。已知平均每小時出生3個嬰兒，請問下一個小時，會出生幾個？

有可能一下子出生6個，也有可能一個都不出生。這是我們沒法知道的。

泊松分佈就是描述某段時間內，事件具體的發生概率。

       上面就是泊松分佈的公式。等號的左邊，P 表示概率，N表示某種函式關係，t 表示時間，n 表示數量，1小時內出生3個嬰兒的概率，就表示為 P(N(1) = 3) 。等號的右邊，λ 表示事件的頻率。接下來兩個小時，一個嬰兒都不出生的概率是0.25%，基本不可能發生。

接下來一個小時，至少出生兩個嬰兒的概率是80%。

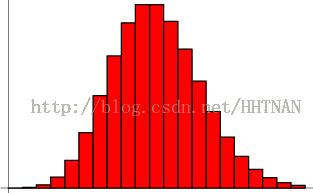
     泊松分佈的圖形大概是下面的樣子。

       可以看到，在頻率附近，事件的發生概率最高，然後向兩邊對稱下降，即變得越大和越小都不太可能。每小時出生3個嬰兒，這是最可能的結果，出生得越多或越少，就越不可能。

二、二項分佈

      二項分佈即重複n次的伯努利試驗。在每次試驗中只有兩種可能的結果，而且是互相對立的，是獨立的，與其它各次試驗結果無關，結果事件發生的概率在整個系列試驗中保持不變，則這一系列試驗稱為伯努利實驗。

三、正太分佈

      正態分佈（Normal distribution），也稱"常態分佈",又名高斯分佈（Gaussian distribution）,最早由A.棣莫弗在求二項分佈的漸近公式中得到。C.F.高斯在研究測量誤差時從另一個角度匯出了它。P.S.拉普拉斯和高斯研究了它的性質。是一個在數學、物理及工程等領域都非常重要的概率分佈，在統計學的許多方面有著重大的影響力。

假設隨機變數X服從一個位置引數為μ、尺度引數為σ的正態分佈，則可以記為：

而概率密度函式為

當μ = 0,σ = 1時的正態分佈是標準正態分佈。

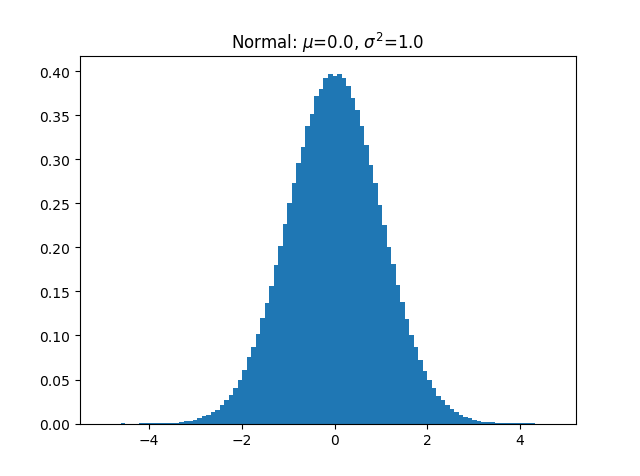
在python中畫正態分佈直方圖

import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
mu ,sigma = 0, 1
sampleNo = 1000000
np.random.seed(0)
s = np.random.normal(mu, sigma, size=sampleNo)

plt.hist(s, bins=100, normed=True)
plt.title('Normal: $\mu$=%.1f, $\sigma^2$=%.1f' % (mu,sigma))
plt.show()

畫直方圖與概率分佈曲線

mu, sigma , num_bins = 0, 1, 50
x = mu + sigma * np.random.randn(1000000)
# 正態分佈的資料
n, bins, patches = plt.hist(x, num_bins, normed=True, facecolor = 'blue', alpha = 0.5)
# 擬合曲線
y = mlab.normpdf(bins, mu, sigma)
plt.plot(bins, y, 'r--')
plt.xlabel('Expectation')
plt.ylabel('Probability')
plt.title('histogram of normal distribution: $\mu = 0$, $\sigma=1$')

plt.subplots_adjust(left = 0.15)
plt.show()