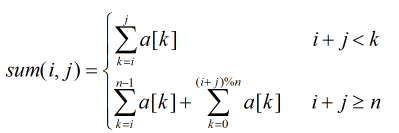(1)有N堆石子，現要將石子有序的合併成一堆，規定如下：每次只能移動任意的2堆石子合併，合併花費為新合成的一堆石子的數量。求將這N堆石子合併成一堆的總花費最小（或最大）。

設dp[i][j]表示第i到第j堆石子合併的最優值，sum[i][j]表示第i到第j堆石子的總數量。那麼就有狀態轉移公式：

當 i = j 時，dp[ i ][ j ] = 0;

當i != j 時，dp[ i ][ j ] = min(dp[i][j], dp[ i ][ k ]+dp[ k+1 ][ j ] ) + sum[ i ][ j ].

程式碼：複雜度為O(n^3).

#include<bits/stdc++.h>
using namespace std;
int a[1010];
int dp[1010][1010];
int sum[1010][1010];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];	
	}
	for(int i=1;i<n;i++)
	{
		sum[i][i]=a[i];
		for(int j=i+1;j<=n;j++)
		{
			sum[i][j]=sum[i][j-1]+a[j];//合併區間i到j的結果
		}
	}
	for(int r=2;r<=n;r++)//區間長度為 r的最小值
	{
		for(int i=1;i<=n-(r-1);i++)//列舉區間長度的開頭
		{ 
			int j=i+(r-1);//區間長度固定，根據開頭求出結尾 
			dp[i][j]=999999999;
			for(int k=i;k<j;k++)//枚舉出合併這段區間以前的最小花費
			{
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
			}
			dp[i][j] += sum[i][j];//加上這一段合併的花費
		}
	}
	cout<<dp[1][n]<<endl;
	return 0;
}
 

因為上面的複雜度為O(n^3)，那麼我們可以利用平行四邊形優化，優化為O(n^2).

程式碼：

#include<bits/stdc++.h>
using namespace std;
int a[1010];
int dp[1010][1010];
int sum[1010][1010];
int p[1010][1010];
int main()
{
	ios::sync_with_stdio(false);
	int n;
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>a[i];	
	}
	for(int i=1;i<n;i++)
	{
		sum[i][i]=a[i];
		for(int j=i+1;j<=n;j++)
		{
			sum[i][j]=sum[i][j-1]+a[j];//合併區間i到j的結果
		}
	}
	
	for(int i=1;i<=n;i++){
		p[i][i]=i;
	}
	
	for(int len=1;len<n;len++)
	{
		for(int i=1;i+len<=n;i++)
		{
			int end = i+len;
			int tmp=0x3ffffff;
			int k=0;
			for(int j = p[i][end-1]; j <= p[i+1][end]; j++)
			{ 
				if(dp[i][j] + dp[j+1][end] + sum[i][end] < tmp)
				{
					tmp=dp[i][j] + dp[j+1][end] + sum[i][end];
					k=j;
				}	
			   
			}
			dp[i][end] = tmp;
			p[i][end] = k;
		}
	}
	/*
	for(int r=2;r<=n;r++)//區間長度為 r的最小值
	{
		for(int i=1;i<=n-(r-1);i++)//列舉區間長度的開頭
		{ 
			int j=i+(r-1);//區間長度固定，根據開頭求出結尾 
			dp[i][j]=999999999;
			for(int k=i;k<j;k++)//枚舉出合併這段區間以前的最小花費
			{
				dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
			}
			dp[i][j] += sum[i][j];//加上這一段合併的花費
		}
	}
	*/
	cout<<dp[1][n]<<endl;
	return 0;
}
 

分析：狀態轉移方程為：

當 j =0 時，dp[i][j]=0.

當 j > 0&& 0<=k < j, dp[i][j]=min(dp[i][j], dp[i][k] + dp[(i+k+1)%n][j-k-1] + sum(i,j).

程式碼：

#include<bits/sdc++.h>

using namespace std;
const int INF = 1 << 30;
const int N = 205;

int mins[N][N];
int maxs[N][N];
int sum[N],a[N];
int minval,maxval;
int n;

int getsum(int i,int j)
{
    if(i+j >= n) return getsum(i,n-i-1) + getsum(0,(i+j)%n);
    else return sum[i+j] - (i>0 ? sum[i-1]:0);
}

void solve(int a[],int n)
{
    for(int i=0;i<n;i++) mins[i][0] = maxs[i][0] = 0;
    
    for(int j=1;j<n;j++)
    {
        for(int i=0;i<n;i++)
        {
            mins[i][j] = INF;
            maxs[i][j] = 0;
            for(int k=0;k<j;k++)
            {
                mins[i][j] = min(mins[i][j],mins[i][k] + mins[(i+k+1)%n][j-k-1] + getsum(i,j));
                maxs[i][j] = max(maxs[i][j],maxs[i][k] + maxs[(i+k+1)%n][j-k-1] + getsum(i,j));
            }
        }
    }
    minval = mins[0][n-1];
    maxval = maxs[0][n-1];
    for(int i=0;i<n;i++)
    {
        minval = min(minval,mins[i][n-1]);
        maxval = max(maxval,maxs[i][n-1]);
    }
}

int main()
{
    while(~scanf("%d",&n))
    {
        for(int i=0;i<n;i++) scanf("%d",&a[i]);
        
        sum[0] = a[0];
        for(int i=1;i<n;i++) sum[i] = sum[i-1] + a[i];
        
        solve(a,n);
        printf("%d %d\n",minval,maxval);
    }
    return 0;
}