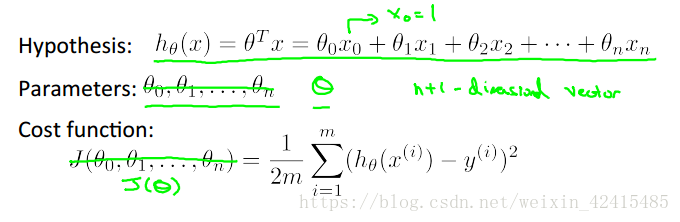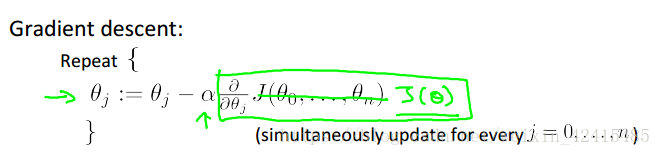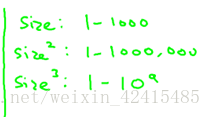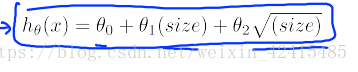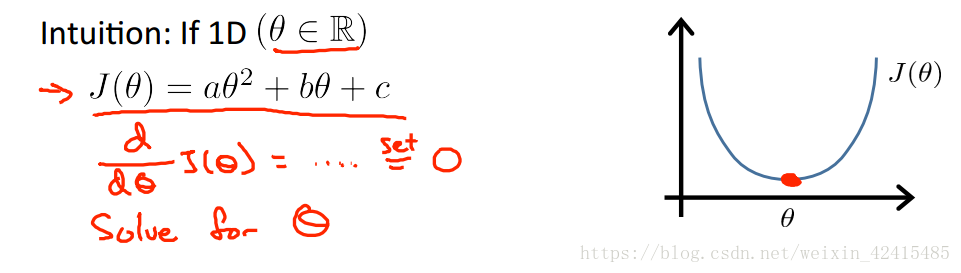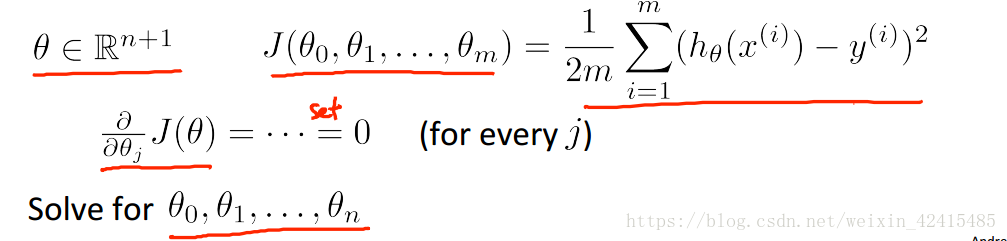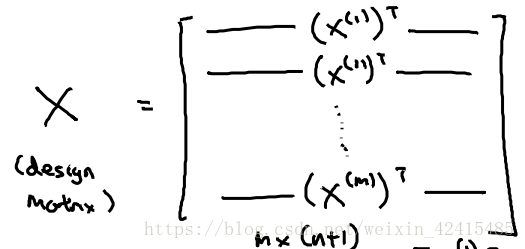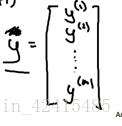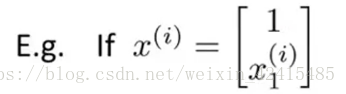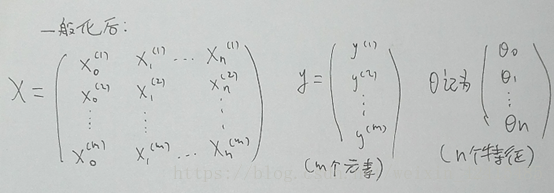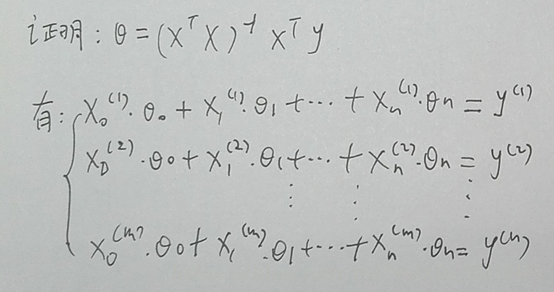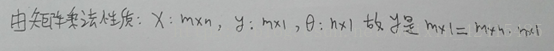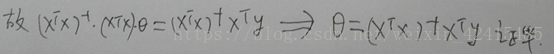吳恩達機器學習學習筆記第五章:多變數線性迴歸
1.Multiple features多特徵
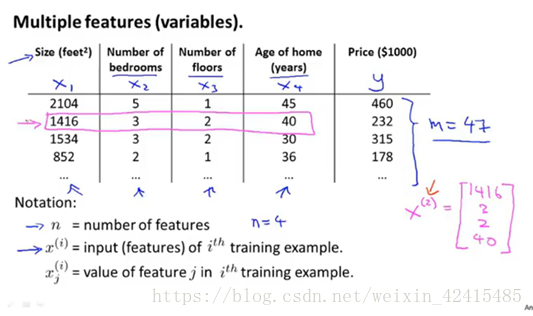
現在我們有多個特徵了,比如還是預測房子價格X不僅僅是面積大小還有臥室數量,樓層數量以及房子的年齡
表達形式的記法:
n=4即有4個特徵(總面積 臥室數量 樓層數 房子年齡)
m=47即有47個樣本(47個房子)
x^(i)表示第i(i不是次方而是對應訓練集的索引)條樣本對的特徵 如x^(2)就是粉色的 這樣表示他就是一個四維向量
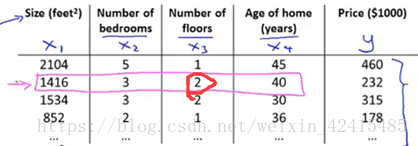
x^(i)j表示:如i=2 j=3就是紅圈
這裡的記號最好能很快反應過來 不然程式設計的時候會比較費時
再來看看線性迴歸的假設函式
Eg是對這個圖Andrew老師把θ舉了個特值的例子:
(Eg是把引數θ取特值的例子)
(一個房子的基本價格是8千,每平方米0.1(百美元),……,-2x4即隨年度使用價錢貶值)
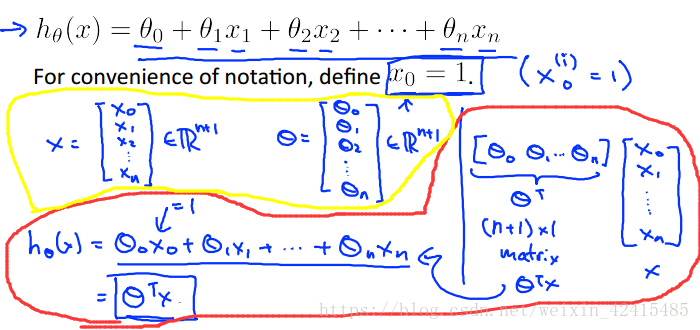
當然特徵個數為n時就如下了:
我們和單變數的做法一樣令他θ0的係數x^(i)0全部=1
所以現在X和θ都是一個n+1維向量 (黃圈)
那麼假設函式就可以寫成內積了(紅圈)
2.多元梯度下降法:
假設函式、引數、代價函式書寫如下:
然後執行梯度下降
左邊是之前學的單變數 右邊是多變數其實本質是一樣的
因為我仍然是線性迴歸我沒有什麼二次項係數這種奇奇怪怪的東西,都是一次的所以θ1~θn求導結果的構造上都是一樣的
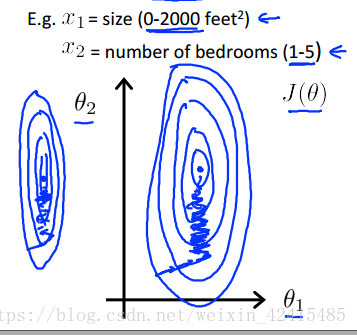
3.多元梯度下降法的特徵縮放:
如果你不同特徵之間的取值範圍差距很大 如面積是0~2000 而寢室數量是1~5
我們畫出來代價函式的等值線就會變成這種又長又扁的橢圓 這會極大的降低我們做梯度下降的速度 並且可能會導致來回波動的情況
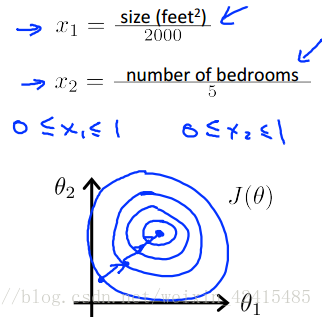
針對這種情況我們就要做特徵縮放:
方法一是用特徵值除以範圍的最大值
這樣做以後等值線就沒有那麼偏移了 看起來更圓了
特徵範圍的設定沒有具體的要求,但是像-100~100、-0.0001~0.0001這種顯然就沒有-3~3、-2~0.5這種好
方法二叫:均值歸一化(Mean normalization)
用X減去均值(μ)除以極差(max-min)
方法三:X減去均值除以標準差(就像標準正態分佈一樣) (正態分佈忘了的可以去找概率論、統計學的書看看)
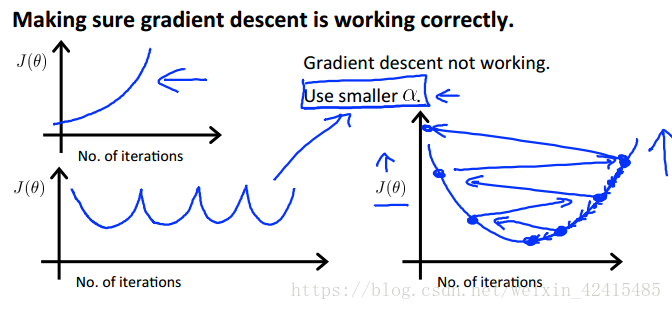
4.多元梯度下降法的學習率:
如果學習率過大,J(θ)可能越來越大甚至不收斂,如果過小,J(θ)的迭代速率會很慢。
這些都是學習率過大的情況(影象的X軸是迭代次數 Y軸是J(θ)的值)
一般認定如果J(θ)迭代中下降到小於某一個值,例如10的負3次方,我們就說他收斂,不需要再進行繼續迭代了,但是這個下界不是那麼好選
如果我們的梯度下降沒有正常工作 那麼檢查學習率 併合理的修正學習率(用嘗試法:若小了就……0.001→0.01→0.1…… 若發現0.01小了 而0.1大了 就試試0.03……)
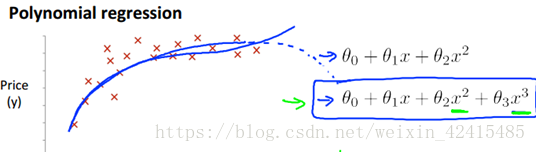
5.特徵和多項式迴歸
除了1階的這種線性迴歸我們還可以弄出2次方、3次方這樣的多項式迴歸
比如有寬度又有長度這兩個 那我們想把長度乘寬度=面積作為特徵去擬合我們的資料
對多項式迴歸 歸一化就非常重要了
6.正規方程
它是一種區別於迭代法用來求θ的直接解法,可以說只需要一步就能求出θ的最優值
對於這種θ是常數的例子直接求導令導數為0就能得到最優解
而下面的θ是n+1維向量,J(θ)是這個向量的函式
如果我對所有θj一個一個的做偏微分那就太蠢了
在樣本中加一列θ0=1 並寫出所有特徵向量Xi對應的矩陣 再把y寫出向量
X是一個m*(n+1)維矩陣 X也稱為設計矩陣(design matrix) 即把每一個訓練樣本
進行轉置後放到每一行
y是一個m維向量 (m是訓練樣本數量 n是特徵變數個數)
設 就能得到使得代價函式最小化的θ
舉個具體的例子:
我的
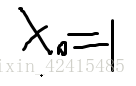
這樣的
上面比較混亂。我們用筆再寫寫書寫表示方法
以及θ=XXXX那個公式線上性代數的證明(書寫較差盡情原諒)
梯度下降法與正規方程法的優缺點對比:
梯度下降法的缺點:
(1)需要選擇學習率a 也就意味著你需要執行多次去找哪個學習率是使執行效果最好的
(2)需要很多次迭代(運算速度就慢了)
梯度下降法的優點:
(1)不管特徵數量是幾千量級還是幾百萬量級,梯度下降法都能很好的工作
(2)除了線性迴歸(Linear Regreesion)外,其他複雜的演算法
正規方程法的優點:
(1)不需要自己找學習率a
(2)不需要迭代
(3)由於不需要找a不需要迭代所以就不需要畫J(θ) 的曲線去檢查收斂性了
(4)不需要進行特徵縮放(我的特徵變數x1是0~1 ,x2是-10000~10000這種都無所謂)
正規方程法的缺點:
(1)正規方程法一般用線上性迴歸上,不適用或者不能用在後續課程中講到的更復雜演算法
(2)當特徵變數太多時會導致運算速度很慢:
正規方程法的計算成本的時間複雜度是O(n^3)
因為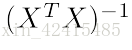
7.正規方程在矩陣不可逆時的解決方法:
首先第一個出現不可逆的原因一般是X裡至少存在一組線性相關的特徵變數比如X1是平方米X2是英尺 1平米=3.28英尺
第二個原因是你有很多特徵具體的說就算m小於或等於n時,譬如說m=10 n=100 θ就算一個101維的向量 你要從10個訓練樣本中找到101個引數值,一般來說很難成功
當出現這種m小於n的情況我們考慮能否刪除一些特徵或者使用一種叫正則化(後面章節會講)的方法
在數值計算這門課中
Python中有numpy.linalg的線性代數庫直接計算這種”偽逆”即:即使矩陣不可逆也能計算出他的逆:
inv(A) 計算方陣A的逆
pinv(A) 計算矩陣A的Moore-Penrose偽逆