在這節中，我們將學習如何對資料進行運算操作。接下來，我們將會使用這些運算操作來實現我們的學習演算法。

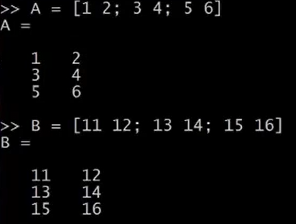
    我現在快速地初始化一些變數。比如設定A為一個3x2的矩陣，B為一個3x2的矩陣，c為一個2x2的矩陣。

    我想算兩個矩陣的乘積，比如計算AxC，只需輸入A*C，這是一個3x2矩陣乘以2x2矩陣，得到這樣一個3x2矩陣。

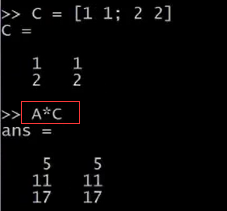
    我們還可以對元素進行運算。當輸入A.*B的時候，會將A中的各個元素與B中對應的元素相乘。通常來說，在Octave中點號一般用來表示元素運算。

    輸入A.^2，這將對矩陣A中的每一個元素進行平方。

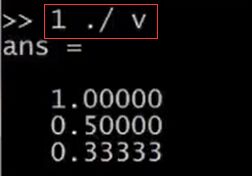
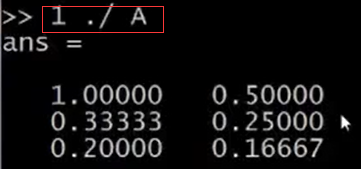
    設v為列向量[1; 2; 3]，可以輸入1./v，得到每一個元素的倒數，所以，就會分別得到1/1 1/2 1/3。矩陣也可以這樣操作，1./A 得到A中每一個元素的倒數。

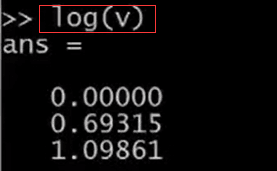
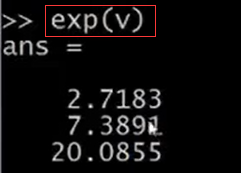
    我們還可以輸入log(v),對v中的所有元素進行求對數運算。exp(v)就是以e為底，以v中的元素為指數的冪運算。

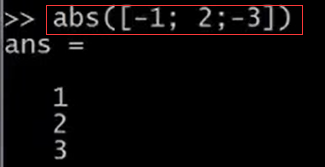
    另外，還可以用abs(v)，對v的每一個元素求絕對值。但是現在v中所有的元素都是正數。我們輸入abs([ -1 ; 2 ; -3 ])，來求這個矩陣的所有元素的絕對值。

    如果輸入-v就會得到v中所有元素的相反數。這等價於-1 * v，但是一般寫成-v就可以了。

    如果我想取出v，並對v中的每個元素都加1。其中一個方法是：首先構造一個3行1列的元素全部為1的向量，然後把這個向量跟原來的向量相加。

    這樣做的依據是：length(v)的值為3，ones(length(v) ,1) 就相當於令ones的大小為3x1。然後再讓它們相加，即v中每個元素都加上1。

    另一種更簡單的方法是：直接用 v+1，v + 1 也就等於把v中的每一個元素都加上1。

    如果想求矩陣A的轉置，我們可以輸入A'（單左引號）這樣我們就能得到A的轉置。如果想求A的轉置的轉置，輸入(A')'那麼我們就會得到原來的矩陣A。

    還有一些有用的函式。我們設a=[1 15 2 0.5]，這是一個1行4列矩陣，讓我們設val=max(a)，這將返回a中最大的元素，也就是15。還可以設[val, ind] =max(a)，這將返回兩個值，val是a中最大的元素，ind是a中該元素的索引。即a中最大的元素為第二個元素，值為15。特別注意：如果你用命令max(A)，而是一個矩陣的話，這樣做就是對每一列求最大值。這個我們之後再討論。

    如果我們輸入a<3，這稱為對應元素比較。這將a中的每一個元素逐個與3進行比較的運算，元素小於3的返回1，否則返回0。

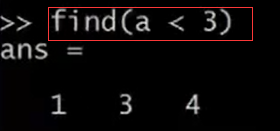
    如果我輸入find(a<3)，這將找出a中哪些元素是小於3的，然後返回它們的索引。

    如果輸入A = magic(3)，magic 函式將返回一個名為幻方矩陣(magic squares)，它們具有以下這樣的數學性質：它們所有的行和列和對角線加起來都等於相同的值。雖然這個函式在機器學習的用處不大，但可以用這個方法很方便地生成一個3x3的矩陣。這些幻方矩陣每行、每列、每個對角線三個數字加起來都是等於同一個數。這是經過數學構造的結果。

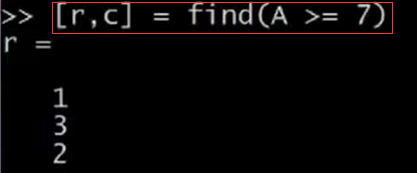
    如果我們輸入[r,c] = find(A>=7)，就會找出A中大於等於7的元素。r和c分別表示行和列，這就表示，第一行第一列的元素大於等於7，第三行第二列的元素大於等於7，第二行第三列的元素大於等於7。

    求和函式：當我們輸入sum(a)，我們就會得到a中所有元素的和。

    如果我想要a中所有元素的乘積，我們就可以輸入prod(a)。它將返回這四個元素的乘積。

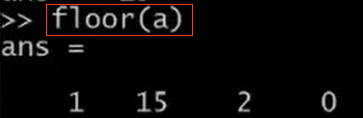
    floor(a) 是向下取整。ceil(a)表示向上取整。

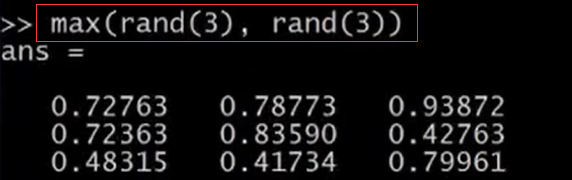
    如果輸入rand(3)，這通常得到一個3×3的隨機矩陣。如果輸入 max(rand(3),rand(3))，它由兩個3×3的隨機矩陣中元素較大值的值組成。所有，你會發現這些元素相對而言都比較大。因為它的每個元素都是取兩個隨機矩陣的對應元素中最大值的結果。

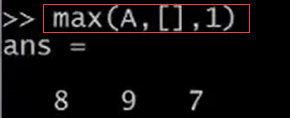
    輸入max(A,[],1)，這樣做會得到每一列的最大值。所以第一列的最大值就是8，第二列是9，第三列的最大值是7，這裡的1表示從A矩陣第一個維度去取值。

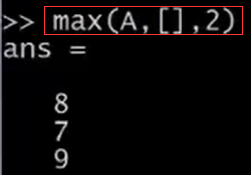
    相對地，如果我鍵入max(A,[],2)，這將得到每一行的最大值，所以，第一行的最大值是等於8，第二行最大值是7，第三行是9。

    可以用這個方法來求得每行或每列的最值。另外，要記住，預設情況下max(A)返回的是每一列的最大值，如果你想要找出整個矩陣A的最大值，你可以輸入max(max(A))，或者你可以將矩陣A轉換成一個向量，然後求最大值，可以輸入max(A(:))，這就是把A轉換成一個向量，並返回向量中的最大值。

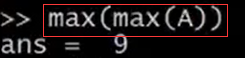
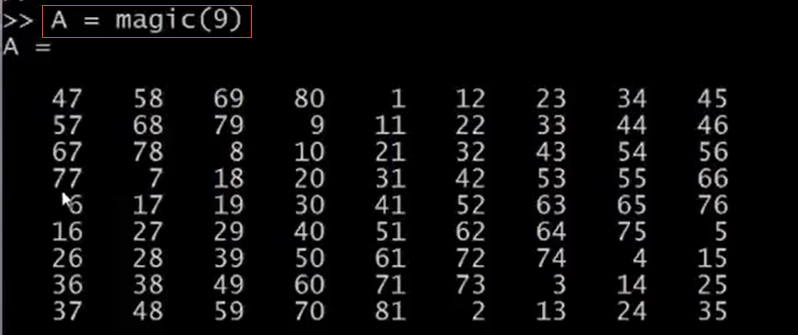
    最後，讓我們把A設計為一個9x9的幻方，幻方的特點是每行每列每對角線的求和都是相等的。這是一個9x9的幻方。

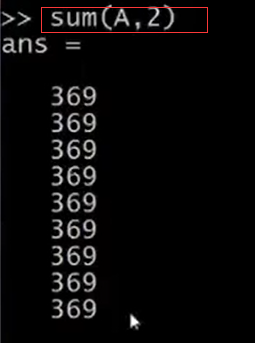
    輸入sum(A,1)，計算每一列的總和，這也驗證了這個幻方每一列加起來都相等，都為369。輸入sum(A,2)，計算每一行的總和，這也驗證了這個幻方每一行加起來都相等，都為369。

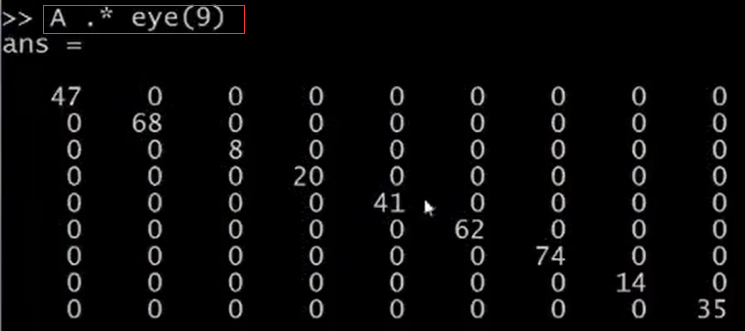
    接著，我們計算對角線的和，確保它們加起來還是同一個數。現在我們要構造一個9x9的單位矩陣，輸入eye(9),然後我們要用A於它元素對應相乘。輸入A.*eye(9)，這樣做的結果是這兩個矩陣對應元素相乘，除了對角線元素外的其他元素都為0。

    然後輸入sum(sum(A.*eye(9))，這實際上是求A的對角線的元素之和，確實是369。

    你也可以求另一條對角線（從左下角到右上角的對角線）的和。我們可以輸入sum(sum(A.*flipup(eye(9)))，其中flipup表示使矩陣垂直翻轉。實際上我們求得另一條對角線和也是369。

    設A=magic(3)。如果你想求A矩陣的逆矩陣，輸入pinv(A)，通常稱為偽逆矩陣，你就把它看成是矩陣A求逆，因此這就是A矩陣的逆矩陣。設 temp = pinv(A)，然後再用temp乘以A，得到的就是單位矩陣，對角線為1，其他元素為0。

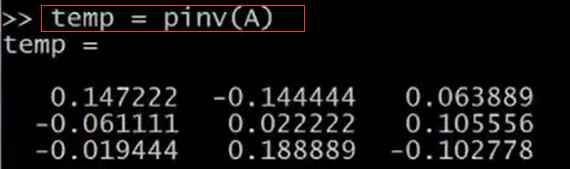
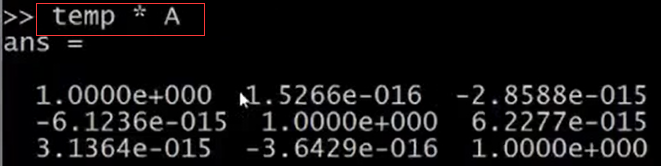
    以上就是對矩陣的元素進行運算的方法。在執行一個學習演算法之後，最有用的事情去觀察結果，或者說讓結果視覺化。在下一節中，我們會學習如何快速將資料視覺化。

&n