引言

博主希望通過最通俗的語言理解感知機，裡面大白話可能比較多，適合剛剛接觸感知機的學習者。大牛請繞路

感知機

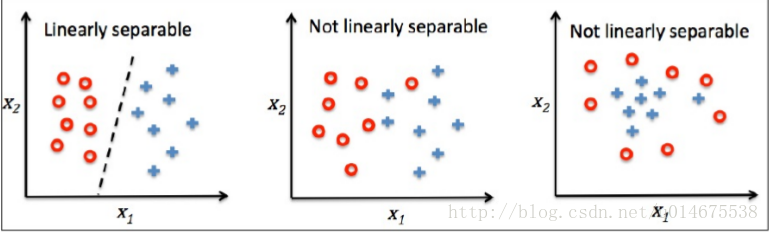
感知機是由兩層神經元組成，其中一層為輸入層，另外一層為輸出層。輸入層用來接收外界的輸入訊號，而輸出層用來將結果輸出。感知機一般用來進行二元資料的分類。感知機的思想主要是通過找到一個超平面，使用這個超平面將資料進行分開。

感知機詳解

例如有一個數據集T={(x1,y1),(x2,y2),(x3,y3)...}，將其資料描述在上圖中，上圖中紅色以及藍色資料為資料集T。我們將其中涉及到的兩個類別記作1(表示正類)和-1(表示負類)。我們通過找到一個超平面即上圖中黑色的直線將資料分開。由於我們可以找到這條直線，因此資料集T為可分資料集。我們使用的直線為

z=wTx
其中，w=[w1,w2,...,wm]T,x=[x1,x2,...,xm]T,我們得到這樣一條直線用於分類，可輸出為一個函式值
那我們怎樣將其歸為哪一個類奧，因此就需要設定閾值，當輸出的函式值y大於設定的閾值，則歸為+1類，否則歸為-1類。在這裡我們使用一個啟用函式，將輸出的y輸入啟用函式，啟用函式就輸出1或者-1.啟用函式到底是什麼呢，我們看下圖，一般使用階躍函式或者是sigmoid函式。


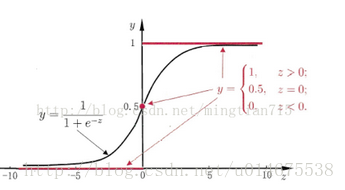
上面的這幅圖就是階躍函式，下面這個就是sigmoid函式，由於階躍函式不連續，因此求導不方便，因此在實際使用過程中基本上都是sigmoid函式。
因為我們現在找到的這條直線可能不是最優的，這句話什麼意思呢，就是對於有些樣本是錯分類的，這裡就不用圖表示，接下來就需要根據輸出結果來調整權重w了。
w

j=wj+Δwj
Δwj=η(y(i)−y(i)⎯⎯⎯⎯⎯)
其中η表示學習速率，通常取值為[0,1]
通過輸出就完成了權重的調整。

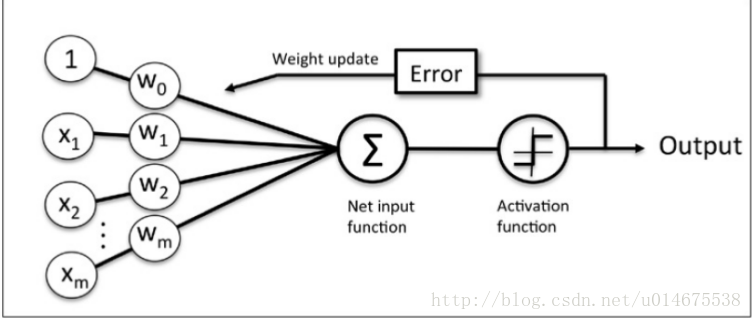
感知機實驗部分

接下來我們使用python動手練習一下

import numpy as np
class Perceptron(object):

    def __init__(self,eta = 0.1,n_iter = 10):
        self.eta = eta
        self.n_iter = n_iter

    def fit(self,X,y):
        self.w_ = np.zeros(1+X.shape[1
 
])
        self.errors = []

        for _ in range(self.n_iter):
            errors = 0
            for feature, target in zip(X, y):
                update =target - self.predict(feature)
                self.w_[1:] += update*feature
                self.w_[0]  += update
                errors += int(update != 0.0)

            self.errors.append(errors)


    def net_input(self,X):
        return np.dot(X,self.w_[1:]+self.w_[0])


    def predict(self,X):
        return np.where(self.net_input(X)>0.0,1,-1)

上面的這一段為演算法的核心程式碼

import pandas as pd

from perceptron.Perceptron import *
from perceptron.plot_decision_region import *

df = pd.read_csv("http://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data",header = None)

y = df.iloc[0:100,4].values
y = np.where(y=='Iris-setosa',-1,1)

X = df.iloc[0:100,[0,2]].values

plt.scatter(X[:50,0],X[:50,1],color = 'red',marker='o',label = 'setosa')
plt.scatter(X[50:100,0],X[50:100,1],color = 'blue',marker='x',label = 'versicolor')
plt.xlabel('petal length')
plt.ylabel('sepal length')
plt.legend(loc = 'upper left')
plt.show()


ppn = Perceptron(eta=0.1,n_iter = 10)
ppn.fit(X,y)

plt.plot(range(1,len(ppn.errors)+1),ppn.errors,marker = 'o')
plt.xlabel('iter')
plt.ylabel('mistakes class')
plt.show()

plot_decision_region(X,y,classifier = ppn)
plt.xlabel('sepal length[cm]')
plt.ylabel('petal length[cm]')
plt.legend(loc = 'upper left')
plt.show()

from matplotlib.colors import ListedColormap
import numpy as np
import matplotlib.pyplot as plt

def plot_decision_region(X,y,classifier,resolution = 0.02):
    markers = ('s','x','o','^','v')
    colors = ('red','blue','lightgreen','gray','cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    x1_min,x1_max = X[:,0].min()-1,X[:,0].max()+1
    x2_min,x2_max = X[:,1].min()-1,X[:,1].max()+1

    xx1,xx2 = np.meshgrid(np.arange(x1_min,x1_max,resolution),
                          np.arange(x2_min,x2_max,resolution))
    Z = classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)

    plt.contourf(xx1,xx2,Z,alpha = 0.4,cmap = cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())

    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x = X[y==cl,0],y = X[y==cl,1],
                    alpha=0.8,c = cmap(idx),
                    marker=markers[idx],label = cl)

總結

感知機對於先行可分的資料集可以適用，對於那些線性不可分的資料無法工作。第2張圖片和第3張就是線性不可分的資料集。對於這些資料的處理，後面會講解處理辦法。