給定多邊形的頂點座標（有序），讓你來求這個多邊形的面積，你會怎麼做？
我們知道，任意多邊形都可以分割為N個三角形，所以，如果以這為突破點，那麼我們第一步就是把給定的多邊形，分割為數個三角形，分別求面積，最後累加就可以了，把多邊形分割為三角形的方式多種多樣，在這裡，我們按照如下圖的方法分割：

圖1

S點作為起始點（點1），a->e依次作為點2,3……。
一個三角形的面積是怎樣的呢？
根據線性代數的知識，我們有如下的三角形面積公式，稱之為有向面積(signed area)：

將這個行列式以第三列展開可以得到：

這就是以點1、2、3構成的三角形的有向面積（點如果是順時針給出，有向面積為負，逆時針給出，有向面積為正

圖2

用剛才的劃分方法的話，就會出現一個詭異的問題，那就是有一個三角形出現在了圖形的外面，而另外一個又超出了多邊形的範圍（劃分為了Sab，Sbc兩個圖形），那麼這樣再用剛才的公式求面積，結果還是正確的麼？
S(1->4)=S(1,2,3)+S(1,3,4)
先公佈結論，這個式子是正確的，等等，為什麼？還記得剛才我提到了那個“有向面積”的概念麼？忘了的話，請回頭看看加重了的字。
請注意從圖中看，Sab點為順時針排列，Sbc點為逆時針排列，面積從數值上就是從Sab這個超過範圍的大三角形中去掉Sbc這個小三角形，最後的結果神奇的就是多邊形Sabc的面積，那麼這個結論能否推廣到任意多邊形呢？

圖3

在這裡不做證明，下面給出的公式，就是任意多邊形的面積公式：

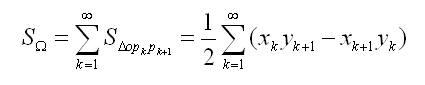
題目：hdu2036     http://acm.hdu.edu.cn/showproblem.php?pid=2036

程式碼：

#include<iostream>
#include<cstdio>
#include<string.h>
#include<math.h>
#include<string>
#include<map>
#include<set>
#include<vector>
#include<algorithm>
#include<queue>
#include<iomanip>
using namespace std;
struct P{
    int x;
    int y;
};
P p[105];
double area(int a)
{
    int b = a-1;
    return (p[b].x*p[a].y-p[a].x*p[b].y)-(p[0].x*p[a].y-p[a].x*p[0].y)+(p[0].x*p[b].y-p[b].x*p[0].y);
}
int main()
{
    int n;
    while(cin >> n){
        if(n==0) break;
        for(int i=0;i<n;i++)
            cin >> p[i].x >> p[i].y;
        double sum = 0;
        for(int i=2;i<n;i++){
            sum += 1.0/2.0*area(i);
        }
        cout << fixed << setprecision(1) << sum << endl;
    }
    return 0;
}