數論選講
一、容斥原理
1.什麼是容斥原理
在計數時,必須注意沒有重複,沒有遺漏。為了使重疊部分不被重複計算,人們研究出一種新的計數方法,這種方法的基本思想是:先不考慮重疊的情況,把包含於某內容中的所有物件的數目先計算出來,然後再把計數時重複計算的數目排斥出去,使得計算的結果既無遺漏又無重複,這種計數的方法稱為容斥原理 ——度娘
2.公式
(1).一般形式
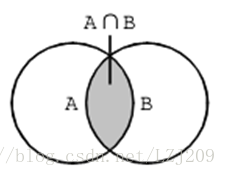
總結一下就是奇數個交就加上,偶數個交就減去。
下面附上兩個圖來幫大家理解一下
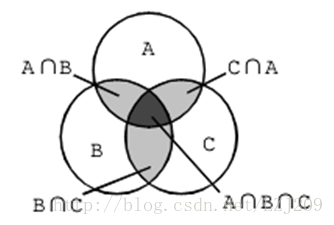
(2).對於數字的形式
這個與莫比烏斯反演有一定的關係,考慮到難度與時間的原因,這裡先不做講解,但是我可以劇透一下,這個只考慮沒有重複質因子的數,然後分奇偶個質因子來考慮加減,一會在講尤拉函式的時候會有涉及。
例題一:bzoj2839
二、擴充套件歐幾里得演算法
1.裴蜀定理
若a,b是整數,且(a,b)=d,那麼對於任意的整數x,y,ax+by都一定是d的倍數,特別地,一定存在整數x,y,使ax+by=d成立。而擴充套件歐幾里得演算法就是用來求這樣一組x,y。
2.演算法原理
當b等於0的時候,a就是最後的gcd(a,b),那麼我們很容易構造出一組x,y即為x=1,y=0,也就是1*a+0*b==a,剩下的我們想辦法通過這組解推出來。
設 ax1+ by1= gcd(a,b);
bx2+ (a mod b)y2= gcd(b,a mod b);
根據樸素的歐幾里德原理有 gcd(a,b) = gcd(b,a mod b);
則:ax1+ by1= bx2+ (a mod b)y2;
即:ax1+ by1= bx2+ (a - [a / b] * b)y2=ay2+ bx2- [a / b] * by2;
也就是ax1+ by1 == ay2+ b(x2- [a / b] *y2);
根據恆等定理得:x1=y2; y1=x2- [a / b] *y2;
3.程式碼
根據上面的推導,我們不難得到這樣的程式碼
int exGcd(int a,int b,int &x,int &y)
{
if(b==0)
{
x=1;y=0;
return a;
}
int r=exGcd(b,a%b,x,y);
int t=x;x=y;y=t-a/b*y;
return r;
}但是我們發現有x,y互換的過程,所以我們稍加改變,就可以得到一個更好看的寫法
int exGcd(int a,int b,int& x,int& y)
{
if 這個程式碼更加的好記,推薦背下來,雖然說不難推,但是考場上最好還是不要浪費時間在這個上QAQ,還有,千萬別亂改這個程式碼,曾經你們的學姐把y-=a/b*x寫成了x*a/b就錯了2333。
現在我們得到的是一組可行的解,我們可以對這個解做出一些調整,現在我們的式子是
三、尤拉函式
1.什麼是尤拉函式
尤拉函式
2.尤拉函式的求法
尤拉函式可以用如下方法求得
這個公式怎麼理解呢?
這是多個二項式乘起來的形式,也就是每項中我挑出來一個乘起來作為最後多項式的部分,那麼我們如果這項選1則代表不選這項,選
3.尤拉函式的性質
(1).尤拉函式是積性函式(這個性質在一會講線性篩的時候會做詳細的解釋)
(2).小於n與n互質的數的和為
證明:如果a與p互質,那麼p-a一定與p互質,則互質的數一定能兩兩組成一個p,證畢。
(3).
證明:相當於列舉n的每一個因數,將n除以這個因數,和這個數互質的數的個數就是和n的gcd為這個因數的數的個數。
4.尤拉定理
當
5.擴充套件尤拉定理
當
6.求尤拉函式的程式碼
long long phi(long long x)
{
long long re=x;
for(int i=2;i<=sqrt(x);i++)
{
if(x%i==0) re-=re/i;
while(x%i==0) x/=i;
}
if(x!=1) re-=re/x;
return re;
}使用線性篩的話可以將求所有尤拉函式的時間優化到O(n),稍後再做講解。
例題二:bzoj4173
四、逆元
1.什麼是逆元?
逆元是在模意義下與
2.逆元的求法
(1).費馬小定理
我們將等式兩邊同時除以一個p得到
所以當a,p互質的時候求a的逆元可以直接算
優點:程式碼簡單,只需一個快速冪
缺點:有侷限性,p必須是質數
(2).尤拉定理
當
由上面的費馬小定理,我們不難想到,a的逆元即為
優點:沒有侷限性。
缺點:程式碼相對比較複雜。
(3).擴充套件歐幾里得演算法
由逆元的性質我們不難得到
我們將這個式子轉換一下,就得到了
我們發現這剛好是(a,p)==1並且求一組可行解使得