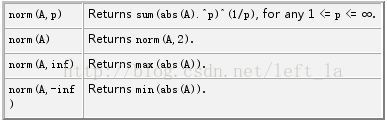
常見向量範數和矩陣範數
1、向量範數
1-範數: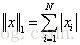
2-範數: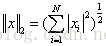
∞-範數: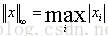
-∞-範數: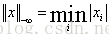
p-範數: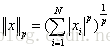
2、矩陣範數
1-範數: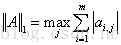
2-範數: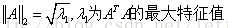
∞-範數: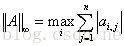
F-範數: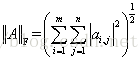
附matlab中norm函式說明
The norm of a matrix is a scalar that gives some measure of the magnitude of the elements of the matrix. The norm function calculates several different types of matrix norms:
n = norm(A) returns the largest singular value of A, max(svd(A)).
n = norm(A,p) returns a different kind of norm, depending on the value of p.
When A is a vector: