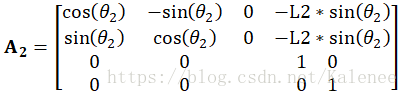機械臂——六軸機械臂逆解
環境:MATLAB 2017B+Robotics Toolbox 9.10.0
前期準備:完成機械臂數學模型的建立+計算機械臂工作空間
注意:這裡採用幾何法計算機械臂逆解,因此不一定適用於其他六軸機械臂構型。
一、運動學分析
連桿變換是機器人進行運動學分析的基礎,其建立主要涉及到座標變換,其中包括座標旋轉和座標平移。
座標旋轉變換為繞座標系的X、Y和Z軸的旋轉變換,一般情況下一個旋轉變換為幾個基本旋轉變換的合成。下面式1為繞X軸旋轉的基本旋轉矩陣,式2為繞Y軸旋轉的基本旋轉矩陣,式3為繞Z軸旋轉的基本旋轉矩陣。
座標平移變換為座標系沿座標軸X、Y和Z軸進行平移轉換,平移轉換後的兩個座標系的原點不同,但座標軸相對平行。式3-4為基本平移矩陣,
為在進行運動學分析過程中,簡化計算,一般將座標轉換矩陣進行齊次變換,轉變為齊次變換矩陣。
通常情況下所有的連桿變換都可以通過座標旋轉和座標平移獲得,即可通過座標旋轉變換和座標平移變換的複合變換獲得連桿變換矩陣。如圖1為兩個座標系的變換,其變換公式為下式
圖1 旋轉和平移複合的一般座標變換
根據前面博文建立的機械臂數學模型,按照各關節座標系的旋轉和平移分別建立對應的齊次連桿變換矩陣:
根據各關節的齊次變換矩陣可計算機器人的位置方程,通過位置方程可以獲取關節變數對機械臂末端姿態的影響。在本課題中,將矩陣到
按順序進行相乘可獲得設計機械臂的位置方程,同時得到機械臂末端相對於基座座標系的位置與姿態。
關節機器人的逆運動學是根據末端位置及姿態求解機器人各關節的角度。與正運動學一組關節角度對應一個末端位姿不同,逆運動學有概率存在機器人末端的某一位姿對應多組關節角度,因此在進行求解的過程中需加入約束條件。
二、逆解計算
圖2 機械臂計算逆解流程圖
上圖為機械臂計算逆解流程圖,逆解計算首先獲取需要機械臂末端執行器到達的位置的座標及其姿態,判斷其位置座標是否在機械臂的工作空間中,如果是才開始進行逆解的計算。
然後將六個關節角度分為兩組,先使用幾何法計算關節角度一、二和三,因為這三個角度可在不涉及角度四、五和六的情況下進行求解。角度一主要控制機械臂整體的旋轉,可投影到XOY座標系進行計算,角度二和角度三與機械臂整體旋轉無關,可投影到座標系XOZ或者YOZ進行計算。此處單純採用幾何法完成關節角的計算,所以受機械臂構型影響較大,無法通用,對其餘構型機械臂參考價值不大,因此此處不列出計算具體流程。完成角度一、二和三計算後,將其結果代入機械臂的DH矩陣中,為後續計算做準備。
接著,計算和
的乘積,並在代入角度一、二和三後計算
、
、
和
的乘積,兩次計算所獲得的結果應該是相等的,因此,根據計算所獲得的矩陣,比較兩邊矩陣內部的各元素,獲取一邊為常數,另一邊為單個未知數的兩個元素,通過求解該單一未知數分別求解角度四、五和六。
因所獲得的解有可能並不唯一,所以最後根據約束條件,對所獲得的解進行篩選,排除不在約束條件內部的解,並根據路徑最短原則選取最優解作為最終的結果。
三、程式實現
%六軸機械臂幾何法反解計算
%流程:輸入末端點座標,檢查是否在工作空間範圍內,計算反解,正解驗證
clc;
clear;
format short;%保留精度
%角度轉換
du=pi/180; %度
radian=180/pi; %弧度
%% 模型匯入
robot_hand;
%% 工作空間計算
figurews;
%% DH引數矩陣
R=[0;0;0];
syms theta1 theta2 theta3 theta4 theta5 theta6
% theta d a alpha
L=[0 L1 0 -pi/2 ;
pi/2 0 -L2 0 ;
0 0 -L3 pi/2 ;
0 L4 0 -pi/2 ;
pi/2 0 0 pi/2 ;
0 L5 0 0 ];
T_start=six_link.fkine([0 0 0 0 0 0]);
q_test=[pi/4 pi/3 pi/3 pi/6 pi/3 pi/4];
T_test_end=six_link.fkine(q_test);
A{1}=trotz(theta1)*transl(0,0,L(1,2))*trotx(L(1,4))*transl(L(1,3),0,0);
A{2}=trotz(theta2)*transl(0,0,L(2,2))*trotx(L(2,4))*transl(L(2,3),0,0);
A{3}=trotz(theta3)*transl(0,0,L(3,2))*trotx(L(3,4))*transl(L(3,3),0,0);
A{4}=trotz(theta4)*transl(0,0,L(4,2))*trotx(L(4,4))*transl(L(4,3),0,0);
A{5}=trotz(theta5)*transl(0,0,L(5,2))*trotx(L(5,4))*transl(L(5,3),0,0);
A{6}=trotz(theta6)*transl(0,0,L(6,2))*trotx(L(6,4))*transl(L(6,3),0,0);
T6=A{1}*A{2}*A{3}*A{4}*A{5}*A{6};
% 輸入末端點座標, 末端姿態預設與初始狀態一致
point_xyz=inputdlg({'X','Y','Z'},'末端點座標',1,{'52.7','0','48.75'});
point_x=str2double(point_xyz{1});
point_y=str2double(point_xyz{2});
point_z=str2double(point_xyz{3});
%% target point
X=point_x;
Y=point_y;
Z=point_z;
Judge_Point_in_WS=0;
if (X<X_max)&&(X>X_min)
if (Y<Y_max)&&(Y>Y_min)
if (Z<Z_max)&&(Z>Z_min)
if (X^2+Y^2+Z^2)<R_max_squre
Judge_Point_in_WS=1;
end
end
end
end
%% ikine
if Judge_Point_in_WS==1
T06=[T_start(1:3,1:3) [X;Y;Z];
0 0 0 1]
T5=T06*inv(A{6});
X_t=double(T5(1,4));
Y_t=double(T5(2,4));
Z_t=double(T5(3,4));
%T45=A{3}*A{4};
%double(T45(3,4));
r_squre=X_t^2+Y_t^2;
r_gen=sqrt(r_squre);
S=Z_t-L1;
R_squre=S^2+r_squre;
R_gen=sqrt(R_squre);
%% solve theta1
theta11=atan2(Y_t,X_t);
theta11=double(real(theta11));
%% solve theta3
a33=sqrt(L3^2+L4^2);
a33_angle=atan(L4/L3);
cos_theta3_bu=(L2^2+a33^2-R_squre)/(2*L2*a33);
theta33=pi-acos(cos_theta3_bu)-a33_angle;
theta33=double(theta33);
%% solve theta2
cos_theta2_bu=(L2^2+R_squre-a33^2)/(2*L2*R_gen);
if S>0
theta22=pi/2-acos(cos_theta2_bu)-atan(S/r_gen);
else
theta22=pi/2-acos(cos_theta2_bu)+atan(-S/r_gen);
end
theta22=double(theta22);
% end
%
%% solve to theta4 theta5 theta6
%% 賦值
A11=trotz(L(1,1)+theta11)*transl(0,0,L(1,2))*trotx(L(1,4))*transl(L(1,3),0,0);
A22=trotz(L(2,1)+theta22)*transl(0,0,L(2,2))*trotx(L(2,4))*transl(L(2,3),0,0);
A33=trotz(L(3,1)+theta33)*transl(0,0,L(3,2))*trotx(L(3,4))*transl(L(3,3),0,0);
%% solve theta4 theta5 theta6
T321=inv(A11*A22*A33);
T45=simplify(A{4}*A{5});
kimejer=simplify(T321*T5);
%% solve theta6
str_solve=kimejer(3,2);%解出theta6 的方程式,if theta6 is right, theta45 then will right
AA=double(subs(str_solve,[cos(theta6),sin(theta6)],[1,0]));
BB=double(subs(str_solve,[cos(theta6),sin(theta6)],[0,1]));
theta66=atan(-AA/BB);
%% solve theta4 and theta5
kimejer2=simplify(subs(kimejer,theta6,theta66));
%% solve theta4
theta441=double(atan(kimejer2(2,1)/kimejer2(1,1)));
if (theta441*radian)<q4_end&&(theta441*radian)>q4_s
theta44=theta441;
end
%% solve theta5
theta551=double(atan2(-kimejer2(3,1),kimejer2(3,3))-pi/2);
if (theta551*radian)<q5_end&&(theta551*radian)>q5_s
theta55=theta551;
end
%% check
theta_ikine=[theta11,theta22,theta33,theta44,theta55,theta66]*radian
T_check=six_link.fkine([theta11 theta22 theta33 theta44 theta55 theta66])
figure (2)
hold on
six_link.plot([theta11,theta22,theta33,theta44,theta55,theta66], plotopt{:});
hold off
end參考:
宋金華. 六軸工業機器人的軌跡規劃與控制系統研究[D].哈爾濱工業大學,2013.
邢婷婷. 上下料機械手的運動學及動力學分析與模擬[D].青島科技大學,2012.
李洪波. 冗餘七自由度串並聯擬人手臂的設計研究[D].河北工業大學,2003.