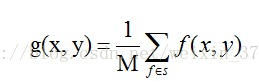openCV之中值濾波&均值濾波(及程式碼實現)
在開始我們今天的部落格之前,我們需要先了解一下什麼是濾波:
首先我們看一下影象濾波的概念。影象濾波,即在儘量保留影象細節特徵的條件下對目標影象的噪聲進行抑制,是影象預處理中不可缺少的操作,其處理效果的好壞將直接影響到後續影象處理和分析的有效性和可靠性。
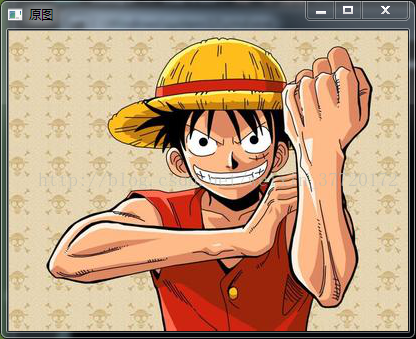
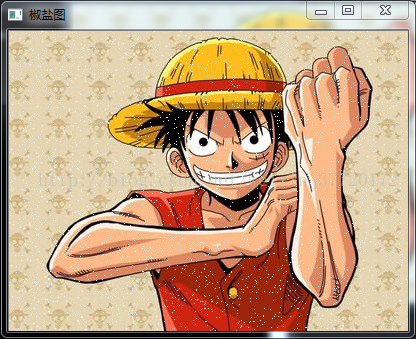
下圖左邊是原圖右邊是噪聲圖:
消除影象中的噪聲成分叫作影象的平滑化或濾波操作。訊號或影象的能量大部分集中在幅度譜的低頻和中頻段是很常見的,而在較高頻段,感興趣的資訊經常被噪聲淹沒。因此一個能降低高頻成分幅度的濾波器就能夠減弱噪聲的影響。
影象濾波的目的有兩個:一是抽出物件的特徵作為影象識別的特徵模式;另一個是為適應影象處理的要求,消除影象數字化時所混入的噪聲。
而對濾波處理的要求也有兩條:一是不能損壞影象的輪廓及邊緣等重要資訊;二是使影象清晰視覺效果好。
平滑濾波是低頻增強的空間域濾波技術。它的目的有兩類:一類是模糊;另一類是消除噪音。
空間域的平滑濾波一般採用簡單平均法進行,就是求鄰近像元點的平均亮度值。鄰域的大小與平滑的效果直接相關,鄰域越大平滑的效果越好,但鄰域過大,平滑會使邊緣資訊損失的越大,從而使輸出的影象變得模糊,因此需合理選擇鄰域的大小。
關於濾波器,一種形象的比喻法是:我們可以把濾波器想象成一個包含加權係數的視窗,當使用這個濾波器平滑處理影象時,就把這個視窗放到影象之上,透過這個視窗來看我們得到的影象。
舉一個濾波在我們生活中的應用:美顏的磨皮功能。如果將我們臉上坑坑窪窪比作是噪聲的話,那麼濾波演算法就是來取出這些噪聲,使我們自拍的面板看起來很光滑。
這篇博文會介紹中值濾波以及均值濾波兩種演算法
一.均值濾波
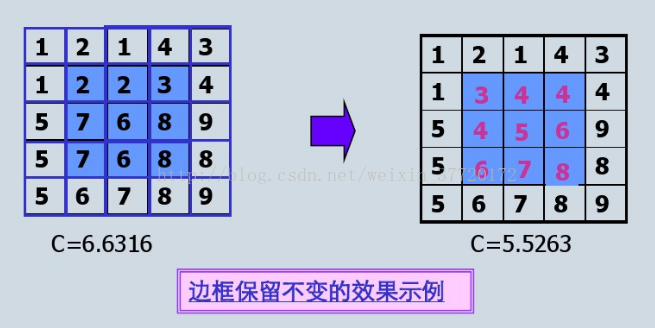
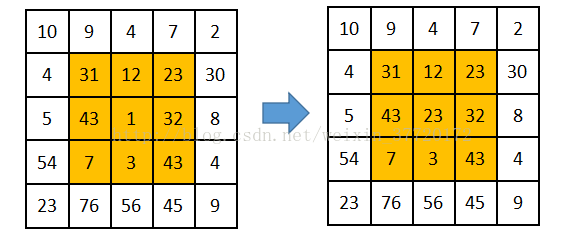
圖片中一個方塊區域(一般為3*3)內,中心點的畫素為全部點畫素值的平均值。均值濾波就是對於整張圖片進行以上操作。
我們可以看下圖的矩陣進行理解
缺陷:均值濾波本身存在著固有的缺陷,即它不能很好地保護影象細節,在影象去噪的同時也破壞了影象的細節部分,從而使影象變得模糊,不能很
實現程式碼:
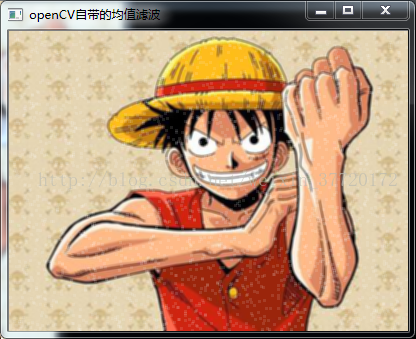
#include "opencv2/imgproc.hpp" #include "opencv2/highgui.hpp" #include<ctime> using namespace cv; using namespace std; //均值濾波 void AverFiltering(const Mat &src,Mat &dst) { if (!src.data) return; //at訪問畫素點 for (int i = 1; i<src.rows; ++i) for (int j = 1; j < src.cols; ++j) { if ((i - 1 >= 0) && (j - 1) >= 0 && (i + 1)<src.rows && (j + 1)<src.cols) {//邊緣不進行處理 dst.at<Vec3b>(i, j)[0] = (src.at<Vec3b>(i, j)[0] + src.at<Vec3b>(i - 1, j - 1)[0] + src.at<Vec3b>(i - 1, j)[0] + src.at<Vec3b>(i, j - 1)[0] + src.at<Vec3b>(i - 1, j + 1)[0] + src.at<Vec3b>(i + 1, j - 1)[0] + src.at<Vec3b>(i + 1, j + 1)[0] + src.at<Vec3b>(i, j + 1)[0] + src.at<Vec3b>(i + 1, j)[0]) / 9; dst.at<Vec3b>(i, j)[1] = (src.at<Vec3b>(i, j)[1] + src.at<Vec3b>(i - 1, j - 1)[1] + src.at<Vec3b>(i - 1, j)[1] + src.at<Vec3b>(i, j - 1)[1] + src.at<Vec3b>(i - 1, j + 1)[1] + src.at<Vec3b>(i + 1, j - 1)[1] + src.at<Vec3b>(i + 1, j + 1)[1] + src.at<Vec3b>(i, j + 1)[1] + src.at<Vec3b>(i + 1, j)[1]) / 9; dst.at<Vec3b>(i, j)[2] = (src.at<Vec3b>(i, j)[2] + src.at<Vec3b>(i - 1, j - 1)[2] + src.at<Vec3b>(i - 1, j)[2] + src.at<Vec3b>(i, j - 1)[2] + src.at<Vec3b>(i - 1, j + 1)[2] + src.at<Vec3b>(i + 1, j - 1)[2] + src.at<Vec3b>(i + 1, j + 1)[2] + src.at<Vec3b>(i, j + 1)[2] + src.at<Vec3b>(i + 1, j)[2]) / 9; } else {//邊緣賦值 dst.at<Vec3b>(i, j)[0] = src.at<Vec3b>(i, j)[0]; dst.at<Vec3b>(i, j)[1] = src.at<Vec3b>(i, j)[1]; dst.at<Vec3b>(i, j)[2] = src.at<Vec3b>(i, j)[2]; } } } //影象椒鹽化 void salt(Mat &image, int num) { if (!image.data) return;//防止傳入空圖 int i, j; srand(time(NULL)); for (int x = 0; x < num; ++x) { i = rand() % image.rows; j = rand() % image.cols; image.at<Vec3b>(i, j)[0] = 255; image.at<Vec3b>(i, j)[1] = 255; image.at<Vec3b>(i, j)[2] = 255; } } void main() { Mat image = imread("路飛.jpg"); Mat Salt_Image; image.copyTo(Salt_Image); salt(Salt_Image, 3000); Mat image1(image.size(), image.type()); Mat image2; AverFiltering(Salt_Image, image1); blur(Salt_Image, image2, Size(3, 3));//openCV庫自帶的均值濾波函式 imshow("原圖", image); imshow("自定義均值濾波", image1); imshow("openCV自帶的均值濾波", image2); waitKey(); }
效果圖:
可以看到圖片變模糊而且噪聲並沒有很有效的去除,該演算法只是模糊化了圖片而已。
二.中值濾波
首先,我們複習中值。在一連串數字{1,4,6,8,9}中,數字6就是這串數字的中值。由此我們可以應用到影象處理中。依然我們在影象中去3*3的矩陣,裡面有9個畫素點,我們將9個畫素進行排序,最後將這個矩陣的中心點賦值為這九個畫素的中值。
程式碼:
//求九個數的中值
uchar Median(uchar n1, uchar n2, uchar n3, uchar n4, uchar n5,
uchar n6, uchar n7, uchar n8, uchar n9) {
uchar arr[9];
arr[0] = n1;
arr[1] = n2;
arr[2] = n3;
arr[3] = n4;
arr[4] = n5;
arr[5] = n6;
arr[6] = n7;
arr[7] = n8;
arr[8] = n9;
for (int gap = 9 / 2; gap > 0; gap /= 2)//希爾排序
for (int i = gap; i < 9; ++i)
for (int j = i - gap; j >= 0 && arr[j] > arr[j + gap]; j -= gap)
swap(arr[j], arr[j + gap]);
return arr[4];//返回中值
}
//影象椒鹽化
void salt(Mat &image, int num) {
if (!image.data) return;//防止傳入空圖
int i, j;
srand(time(NULL));
for (int x = 0; x < num; ++x) {
i = rand() % image.rows;
j = rand() % image.cols;
image.at<Vec3b>(i, j)[0] = 255;
image.at<Vec3b>(i, j)[1] = 255;
image.at<Vec3b>(i, j)[2] = 255;
}
}
//中值濾波函式
void MedianFlitering(const Mat &src, Mat &dst) {
if (!src.data)return;
Mat _dst(src.size(), src.type());
for(int i=0;i<src.rows;++i)
for (int j=0; j < src.cols; ++j) {
if ((i - 1) > 0 && (i + 1) < src.rows && (j - 1) > 0 && (j + 1) < src.cols) {
_dst.at<Vec3b>(i, j)[0] = Median(src.at<Vec3b>(i, j)[0], src.at<Vec3b>(i + 1, j + 1)[0],
src.at<Vec3b>(i + 1, j)[0], src.at<Vec3b>(i, j + 1)[0], src.at<Vec3b>(i + 1, j - 1)[0],
src.at<Vec3b>(i - 1, j + 1)[0], src.at<Vec3b>(i - 1, j)[0], src.at<Vec3b>(i, j - 1)[0],
src.at<Vec3b>(i - 1, j - 1)[0]);
_dst.at<Vec3b>(i, j)[1] = Median(src.at<Vec3b>(i, j)[1], src.at<Vec3b>(i + 1, j + 1)[1],
src.at<Vec3b>(i + 1, j)[1], src.at<Vec3b>(i, j + 1)[1], src.at<Vec3b>(i + 1, j - 1)[1],
src.at<Vec3b>(i - 1, j + 1)[1], src.at<Vec3b>(i - 1, j)[1], src.at<Vec3b>(i, j - 1)[1],
src.at<Vec3b>(i - 1, j - 1)[1]);
_dst.at<Vec3b>(i, j)[2] = Median(src.at<Vec3b>(i, j)[2], src.at<Vec3b>(i + 1, j + 1)[2],
src.at<Vec3b>(i + 1, j)[2], src.at<Vec3b>(i, j + 1)[2], src.at<Vec3b>(i + 1, j - 1)[2],
src.at<Vec3b>(i - 1, j + 1)[2], src.at<Vec3b>(i - 1, j)[2], src.at<Vec3b>(i, j - 1)[2],
src.at<Vec3b>(i - 1, j - 1)[2]);
}
else
_dst.at<Vec3b>(i, j) = src.at<Vec3b>(i, j);
}
_dst.copyTo(dst);//拷貝
}
void main() {
Mat image = imread("路飛.jpg");
Mat Salt_Image;
image.copyTo(Salt_Image);
salt(Salt_Image, 3000);
Mat image3, image4;
MedianFlitering(Salt_Image, image3);
medianBlur(Salt_Image, image4, 3);
imshow("自定義中值濾波處理後", image3);
imshow("openCV自帶的中值濾波", image4);
waitKey();
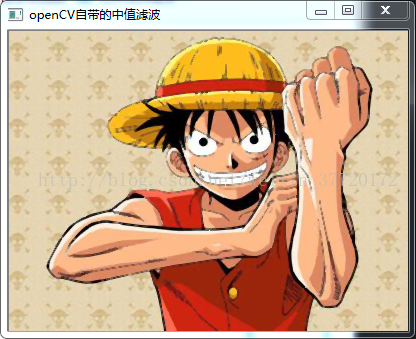
}效果圖:
可以看到,椒鹽噪聲很好的被平滑了,而且也沒均值那樣模糊化太過於嚴重。
希望能賞個臉關注下: