角度與弧度

角度概念：

公共端點的兩條射線組成的圖形叫做角，這個公共點叫做角的頂點，這兩條射線叫做角的邊。
在平面內，一條射線繞它的端點旋轉有兩個相反的方向，逆時針旋轉的角叫做正角，順時針旋轉的角叫做負角。沒有旋轉叫做零角。

弧度概念：

角是由射線繞它的端點旋轉而形成的，在旋轉的過程中，射線上的任一點必然形成一條圓弧。不同點形成的圓弧的長度是不同的，但同一圓心角所對的弧與它所在圓的半徑的比值是固定的，所以可以通過圓的半徑作為單位去度量弧。

角度制：

把圓周360等分，一分是1度，60分等於1度，60秒等於1分。

例如：333°33′33″

弧度制：

長度等於半徑長的圓弧所對的圓心角叫做1弧度的角。

例如：在半徑為r的圓中，弧長為l的弧所對圓心角為α，則α=lr。

為什麼要分角度制與弧度制：

就是為了使每個角都有唯一的一個實數（角度數或弧度數）與它對應；反過來，每一個實數也都有唯一的一個角和它對應。

例如：因為角度制是60進位制，遇到35°6′這樣的角，應該把它化為10進位制的數值35.1°。但是弧度數就
不存在這個問題，因為弧度數是十進位制的實數。

實數：實數包括有理數和無理數。其中無理數就是無限不迴圈小數，有理數就包括整數和分數。實數直觀地定義為和數軸上的點一一對應的數。

常見的弧度：

360°=2π，180°=π，90°=π2，0°=0。

三角函式

三角函式定義：

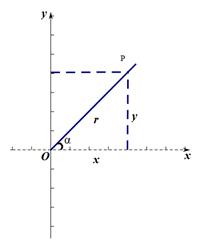
如上圖所示：

正弦：sin α = yr

餘弦：cos α = xr

正切：tan α = yx

正割：sec α = 1cosα = rx

餘割：csc α = 1sinα = ry

餘切：cot α = 1tanα = xy

簡單關係式：

sin²α + cos²α = 1

tan α = sinαcosα

cos(α-β) = cosα·cosβ+sinα·sinβ

sin(α+β) = sinα·cosβ+cosα·sinβ

sin(α-β) = sinα·cosβ-cosα·sinβ

tan(α+β) = tanα+tanβ1−tanα⋅tanβ

tan(α-β) = tanα−tanβ1+tanα⋅tanβ

sin2α = 2sinα·cosα

cos2α = cos²α-sin²α = 1-2sin²α = 2cos²α - 1

tan2α = 2tanα1−tanα

cosα·cosβ = 12[cos(α+β)+cos(α-β)]

sinα·sinβ = 12[cos(α-β)-cos(α+β)]

sinα·cosβ = 12[sin(α+β)+sin(α-β)]

cosx+cosy = 2·cosx+y2·cosx−y2

cosx-cosy = -2·sinx+y2·sinx−y2

sinx+siny = 2·sinx+y2·cosx−y2

sinx-siny = 2·cosx+y2·sinx−y2

sin²α=1−cos2α2

cos²α=1+cos2α2