有關模糊pid的相關知識就把自己從剛接觸到模擬出結果看到的大部分資料總結一下，以及一些自己的ps

以下未說明的都為轉載內容

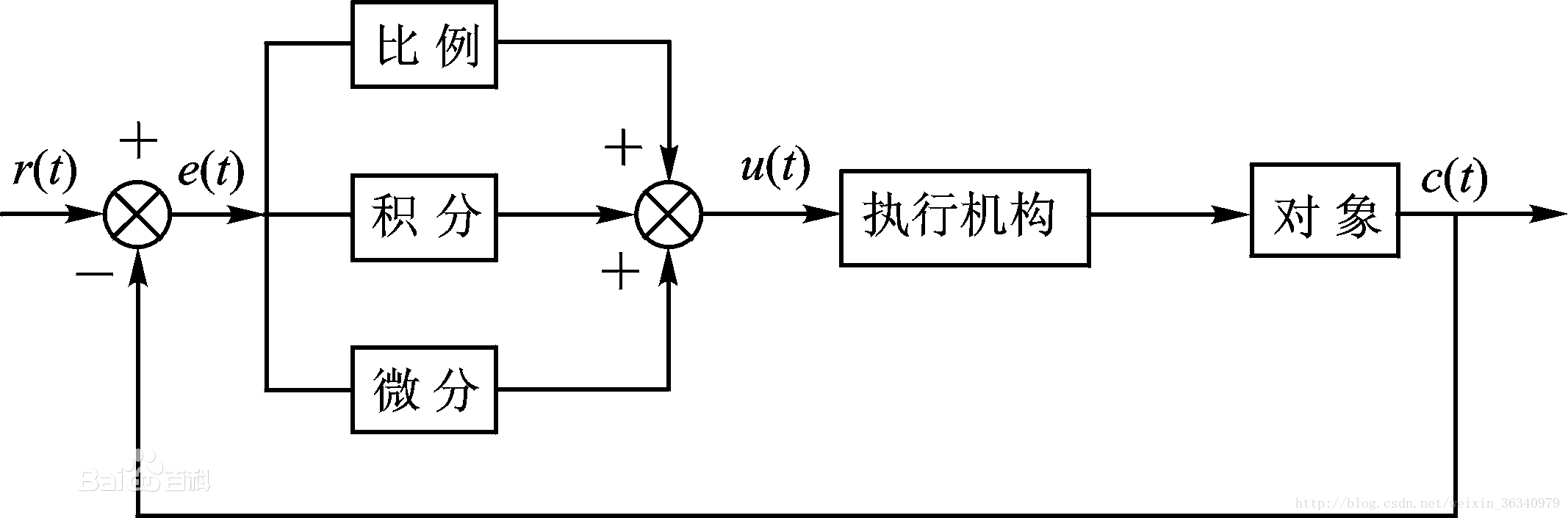
在講解模糊PID前，我們先要了解PID控制器的原理（本文主要介紹模糊PID的運用,對PID控制器的原理不做詳細介紹）。PID控制器（比例-積分-微分控制器）是一個在工業控制應用中常見的反饋迴路部件，由比例單元P、積分單元I和微分單元D組成。PID控制的基礎是比例控制；積分控制可消除穩態誤差，但可能增加超調；微分控制可加快大慣性系統響應速度以及減弱超調趨勢。

1.1傳統PID控制

 傳統PID控制器自出現以來，憑藉其結構簡單、穩定性好、工作可靠、調整方便等優點成為工業控制主要技術。當被控物件的結構和引數具有一定的不確定性，無法對其建立精確的模型時，採用PID控制技術尤為方便。PID控制原理簡單、易於實現，但是其引數整定異常麻煩。對於小車的速度控制系統而言，由於其為時變非線性系統不同時刻需要選用不同的PID引數，採用傳統的PID控制器，很難使整個執行過程具有較好的執行效果。

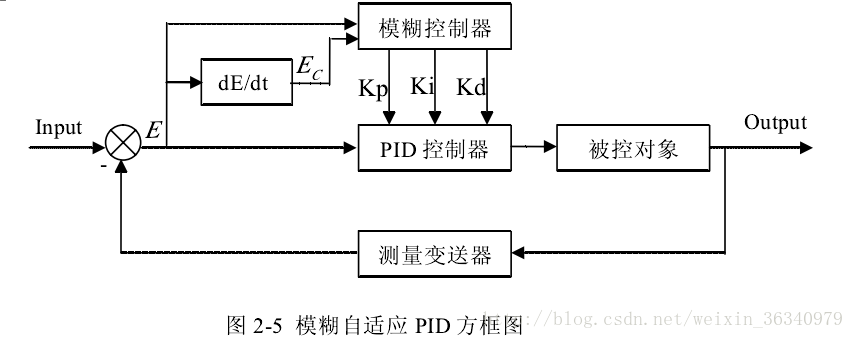
1.2模糊PID控制

 模糊PID控制，即利用模糊邏輯並根據一定的模糊規則對PID的引數進行實時的優化，以克服傳統PID引數無法實時調整PID引數的缺點。模糊PID控制包括模糊化，確定模糊規則，解模糊等組成部分。小車通過感測器採集賽道資訊，確定當前距賽道中線的偏差E以及當前偏差和上次偏差的變化ec，根據給定的模糊規則進行模糊推理，最後對模糊引數進行解模糊，輸出PID控制引數。

2.1模糊化

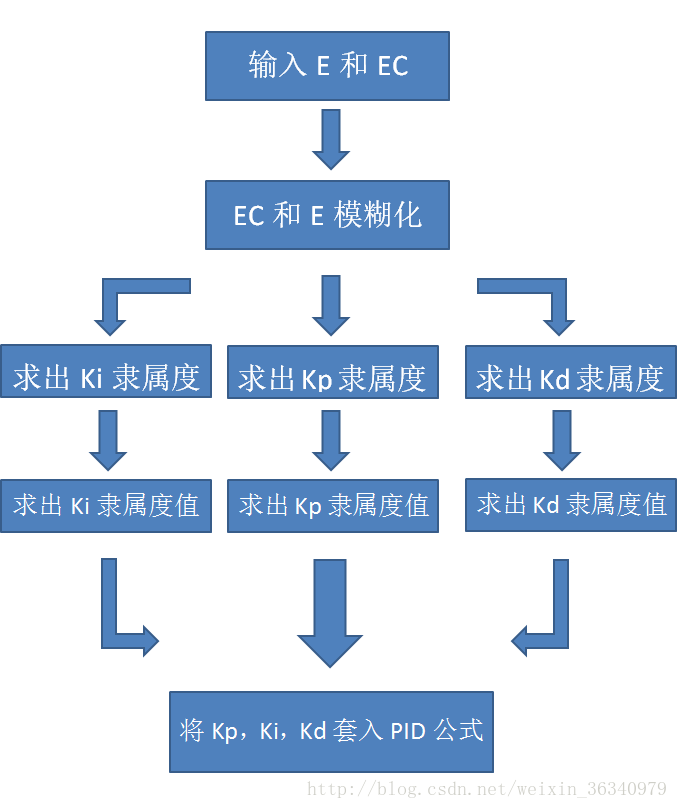
 模糊控制器主要由三個模組組成：模糊化，模糊推理，清晰化。具體如下圖所示。而我們將一步步講解如何將模糊PID演算法運用到智慧車上。（最好用筆一步步自己寫一遍！！！）

 首先我們的智慧車會採集到賽道的相關資料，例如攝像頭車，其採集到的資料經過演算法處理之後會得到與中線的偏差E，以及當前偏差和上次偏差的變化（差值）EC兩個值（即此演算法為2維輸入，同理也可以是1維和3維，但2維更適合智慧車）。例如此時車偏離中線的距離為150，而上一時刻偏離中線的距離為120，則E為150，EC為150 - 120 = 30。

 其次我們要對這兩個值進行模糊化。這裡我們對E進行舉例。攝像頭車採集回來的E是有範圍的，即與中線的偏差是在一個區間內可行的。在這裡我們假設該區間為-240到240，即小車偏離中線的最大距離為240，正負即為左右。再假設中線偏差變化率的可行區間為-40到+40。

        接著我們要對這兩個值進行模糊化。我現在將E的區間（-240 到 240）分成8個部分，那麼他們分別為-240 ~ -180，-180 ~ -120 ，-120 ~ -60，-60 ~ 0，0 ~ 60，60 ~ 120，120 ~ 180，180 ~ 240。然後我們把-180，-120，-60，0，60，120，180分別用NB，NM，NS，ZO，PS，PM，PB表示（個人理解N為negative，P為positive，B為big，M為middle，S為small，ZO為zero）。例如，當E = 170時，此時的E屬於PM和PB之間，而此時的E也會對應2（或1）個隸屬度。E隸屬於PM（120）的百分比為（180 - 170） /  （180 - 120） = 1 / 6 ，而同理隸屬於PB（180）的百分比為（170 - 120） / （180 - 120） = 5 / 6  。意思就是120到180進行線性分割了，E離PM和PB哪個更近，則隸屬於哪個就更大（當輸出值E大於180（PB）時，則隸屬度為1，隸屬度值為PB，即E完全隸屬於PB，同理當E小於 - 180 （NB）時也一樣）。同理也可以對EC進行模糊化。

2.2 模糊推理

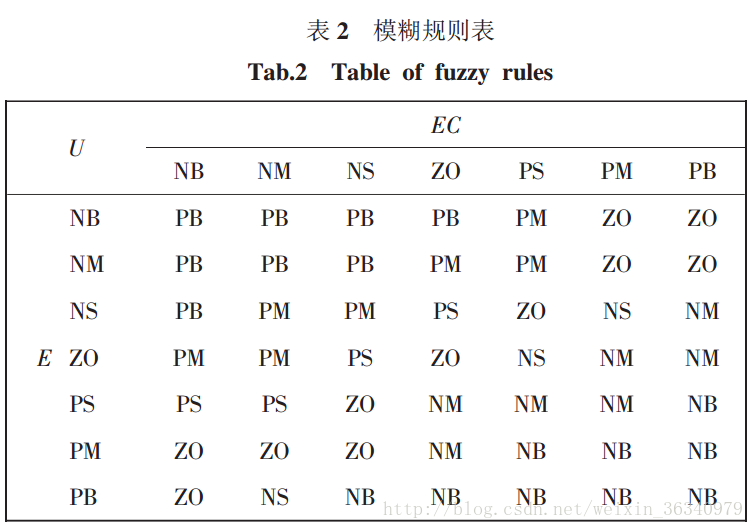
       對於採集回來的E和EC，我們可以推出它們各所佔的隸屬度，此時我們可以根據模糊規則表去找出輸出值所對應的隸屬度。

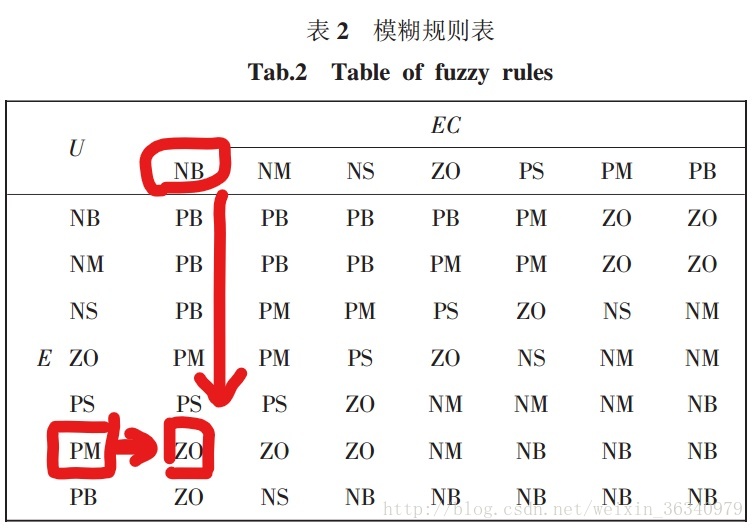
     我們假設為E的兩個隸屬度值為PM、PB,E屬於PM的隸屬度為a（a < 1），則屬於PB的隸屬度為（1 - a）。再假設EC的兩個隸屬度值為NB、NM，EC屬於NM的隸屬度為b，則屬於NB的隸屬度為（1 - b）。而在假設中，E屬於PM的隸屬度為a，EC屬於NB的隸屬度為( 1 - b )，則輸出值屬於ZO的隸屬度為a *( 1 - b )（看圖）。

       同理我們可以得出，當輸出值屬於ZO的另外兩個隸屬度為a * b， （ 1 - a ） * （ 1 - b） ，而輸出值屬於NS的隸屬度為（ 1 - a ） * 1 - b。

       在這裡我們先證明一個條件，將這四個隸屬度加起來，剛好等於1。這是因為

        （a + （1 - a）） * （b + （1 - b）） = a * b + ( 1 - a ) *  b  + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b )   （下圖）

       即一個十字相乘的概念。這個等式說明輸出值的隸屬度之和等於1（第三步求解的時候需要用到隸屬度之和）。

因此，我們知道了輸出值為ZO的隸屬度和為 a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ，輸出值為NS的隸屬度為 ( 1 - a ) *  b 。

2.3 清晰化

       對於輸出值，我們同樣採用給予隸屬度的辦法。例如，我們把輸出值假設為[1000，1400]（即舵機的擺角值範圍）的區間同樣劃分為八個部分，即7個隸屬值NB,NM,NS,ZO,PS,PM,PB。根據上一步所得出的結論，我們就可以用隸屬度乘以相應的隸屬值算出輸出值的解，即 （a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ） * ZO   +    ( 1 - a ) *  b * NS。到此為止，整個模糊過程就結束了。

3 模糊PID

      我們已經知道了整個模糊的過程，但上述的過程還不夠完美。因為我們的輸出值只有一個輸出，並沒有實現PID。因此我們可以先對E和EC進行模糊化，然後分別對kp和ki和kd（PID的三個引數）進行求解，再套入公式。

     一般的我們也可以只用kp，kd，不用ki。而模糊規則表一般的論文已經基本給出。因此帶入演算法之後我們的難度也只是在於調節kp，kd，和適當調節規則表。當然調節的難度會大於普通的PID，因為還要定kp，kd的輸出範圍，調得不好可能效果並沒有普通的PID好。

4. 部分解釋

     4.1對於部分論文所說的重心法解模糊，其實就是上述方法。公式如下。

      式中μ（Zi） * Zi相當於文章上面的（a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ） * ZO   +    ( 1 - a ) *  b * NS，即隸屬度乘以隸屬度值之和，而μ（Zi）之和就是輸出值的隸屬度之和，我們已經證明它是等於1的

PS:模糊控制表在相關書籍中都有，都是前輩的經驗，一般的無需修改即可，不過如果自己要配自己的資料也可以自己配，邏輯關係理清楚就可以了，反正我自己理來理去還是挺鍛鍊對pid三個變數的理解的，當然不止pid,模糊控制也可以單獨使用，很靈活的，重點就是各個引數範圍確定，這是影響模糊控制最重要的因素。

matlab版本：matlab2010b

第一步：利用matlab模糊控制工具箱設計模糊控制器。

1、在matlab命令視窗中輸入 fuzzy ，產生如下視窗。

2、確定模糊控制器結構，即根據具體的系統確定輸入、輸出量。

這裡我們可以選取標準的二維控制結構，即輸入為誤差e和誤差變化ec，輸出為控制量u。輸入變數的新增通過 Edit -> Add Variable -> Input 實現。

3、語言值及隸屬函式的確定。

首先我們要確定描述輸入輸出變數語言值的模糊子集，如{NB，NM，NS，ZE，PS，PM，PB}，並設定輸入輸出變數的論域，例如我們設定誤差E、誤差變化EC的論域為[-6 6]，控制量U的論域為[-10 10]；然後為模糊語言變數選取相應的隸屬度函式。通過 Edit -> Membership Functions 開啟隸屬度函式編輯器，然後分別對輸入輸出變數定義論域範圍，新增隸屬函式，以E為例，設定論域範圍為[-6 6]，新增隸屬函式的個數為7。（注：隸屬度函式編輯器初始時已為每個變數定義了3個隸屬函式，再通過 Edit -> Add MFs 新增隸屬函式時，個數選擇4即可）

4、模糊控制規則的制定。

對於我們這個二維控制結構以及相應的輸入模糊集，我們可以制定49條模糊控制規則。

5、解模糊。

模糊控制器的輸出量是一個模糊集合，通過解模糊化方法判決出一個確切的精確量，解模糊化方法很多，我們這裡選取重心法。

6、儲存建立的模糊控制器。

File -> Export -> To File，檔名為 fuzzy_control。

第二步：建立Simulink模型。

1、在matlab命令視窗中輸入simulink，產生如下視窗。

2、新建模糊控制器模型，樣式如下。

3、在matlab命令視窗下輸入 fuzzy = readfis('fuzzy_control') ，將之前建立的模糊控制器載入到工作空間，並將Fuzzy Logic Contrtoller的引數設定為fuzzy。

4、儲存該模型，命名為 fuzzy_model

第三步：系統測試介面的設定。

1、通過 Tools -> System Test -> Launch System Test 進入系統測試介面。

2、新增測試模型。

滑鼠選中Main Test ，選單欄 Insert -> Test Element -> Simulink ，選擇第二步中建立的模型 fuzzy_model 。

3、變數定義。

在Test Vectors 項裡定義兩個測試向量，變數名分別為 input1、input2，input1 = [-6:1:6]， input2 = [-6:1:6]；在Test Variables 裡定義測試變數，變數名為output。

4、變數對映。

把測試向量input1、input2分別對映到模糊控制器的輸入口 in1、in2，做為輸入測試訊號。把測試變數 output 對映到模糊控制器輸出口out1。設定後的介面如下：

輸入測試向量到模糊模型輸入口對映：

模糊控制器輸出儲存對映：

5、測試資料儲存。

在測試介面點Save Results項，設定如下：

6、執行測試，注意在Main Test(169 Iterations）(169次迭代，運算代價),等待測試結束。

第四步：模糊控制查詢表的生成

1、系統測試結果儲存在 stresults.ResultsDataSet.output 中，為169*1 cell的單元陣列。（注：單元cell為 [n*1 double] 結構，表示系統被測試了n次）。

2、在matlab命令視窗下輸入 test_data = stresults.ResultsDataSet.output ，將測試結果另存在變數 test_data 中。

3、測試結果格式轉換。

由於所建的二維查詢表為13行13列，所需的資料應該為13*13 double陣列，但因為test_data為 169*1 cell 的單元陣列，無法直接作為表格資料輸入，因此需先進行格式轉換。

在matlab命令視窗下輸入 table_data = Cell2Array( test_data ,  1 , 13 , 13 ) ，呼叫Cell2Array函式，取每個單元陣列中的第一行元素，即第一次測試資料，返回結果儲存在 table_data 中。

原始碼如下：

4、新建二維查詢表模型，樣式如下：

5、點開二維查詢表進行如下設定：

6、點 Edit 按鈕，即可檢視所生成的表格。 

PS：以上兩篇就是我基本完成的教程了，matlab因為自己不怎麼熟，所以折騰了挺久的，基本就是從matlab什麼都不懂到可以完成這個模擬，然後我也把新手可能出現的一些問題講講吧。

看了第一篇之後到matlab模糊控制器的設定儲存應該問題不大，之後就是建立模擬模型，因為從來沒用過所以一竅不通，我的版本是2016b,介面也和上面的有些不同，可是吃了點苦頭，所以以下就是給新手看看的，不要笑我教的簡單哈

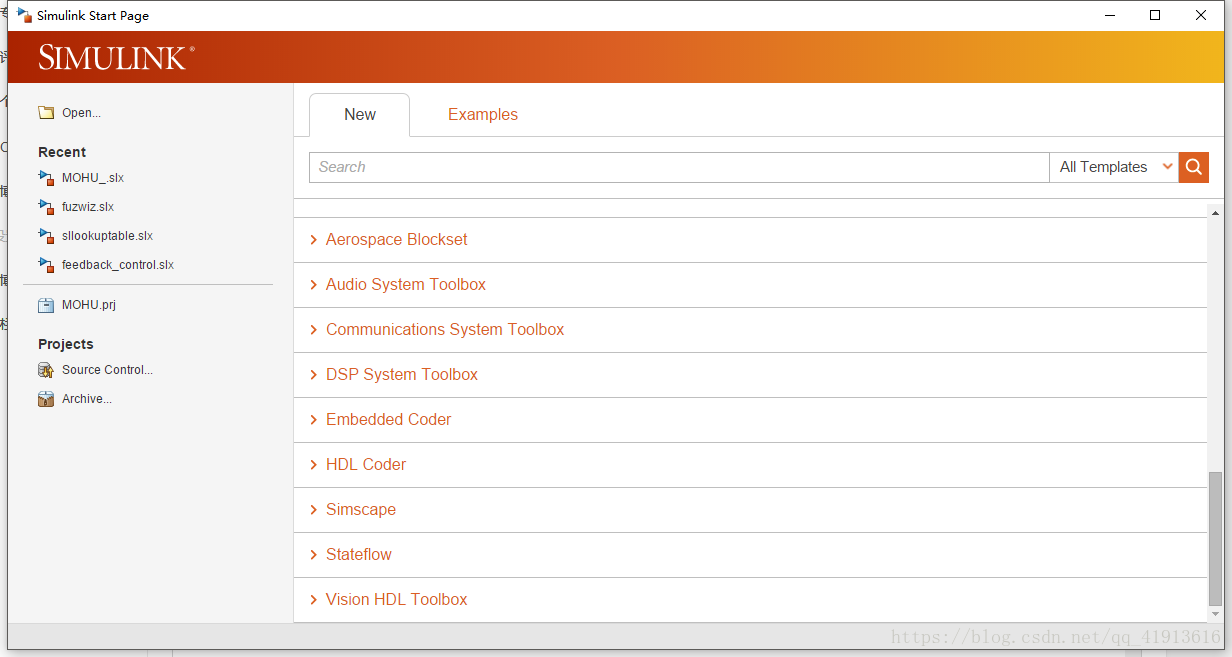
首先，simulink介面不同，我的是新版的

是這樣的介面，剛開始一臉懵逼不知道怎麼建立模擬模型

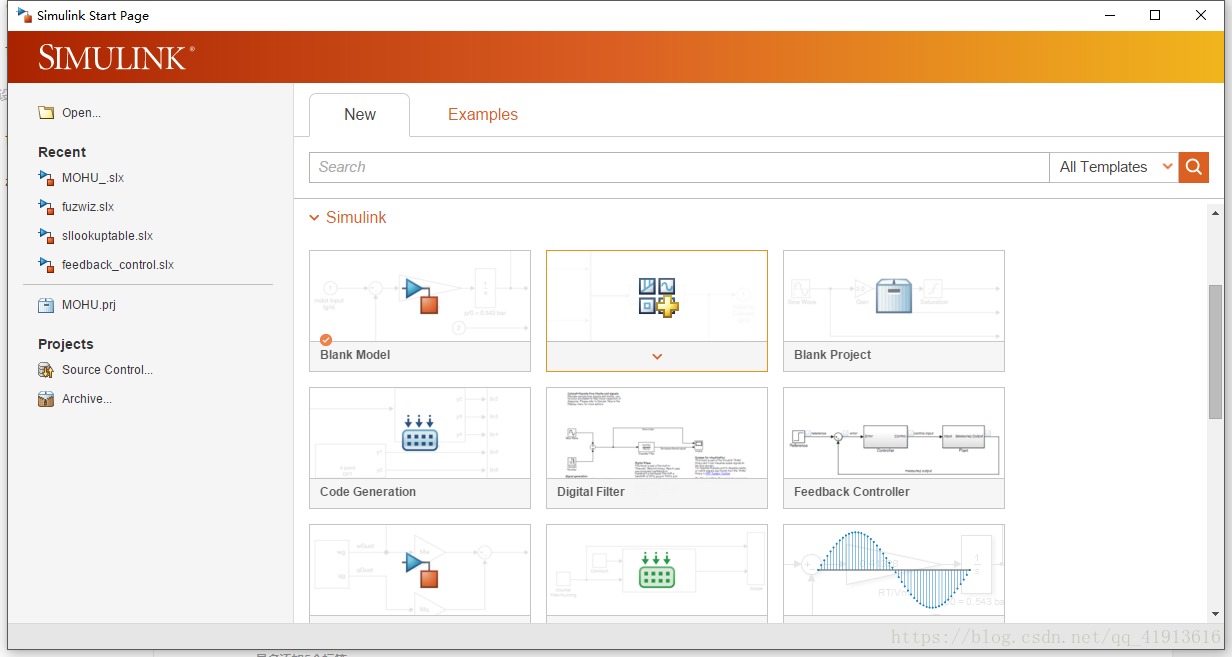
之後隨便點一個建立一個新的就好

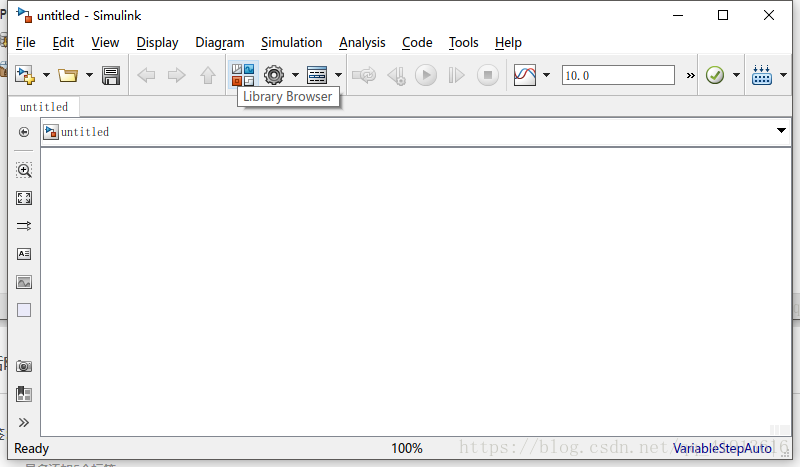
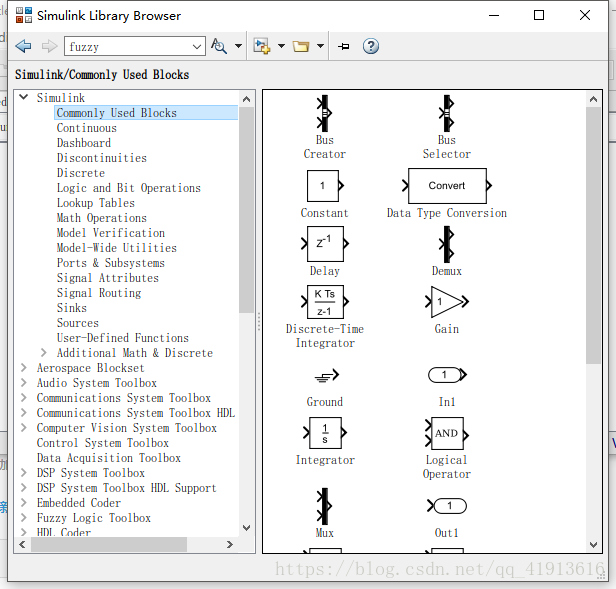
這個介面之後點那個Library Browser,裡面有需要的元素，你就按上面那個圖把元素都複製過來就好

注意那個fuzzy的圖示，改變輸出的個數是雙擊它有選項，我當初找了半天硬是找不到，，

把該加的東西都放進去，連線好

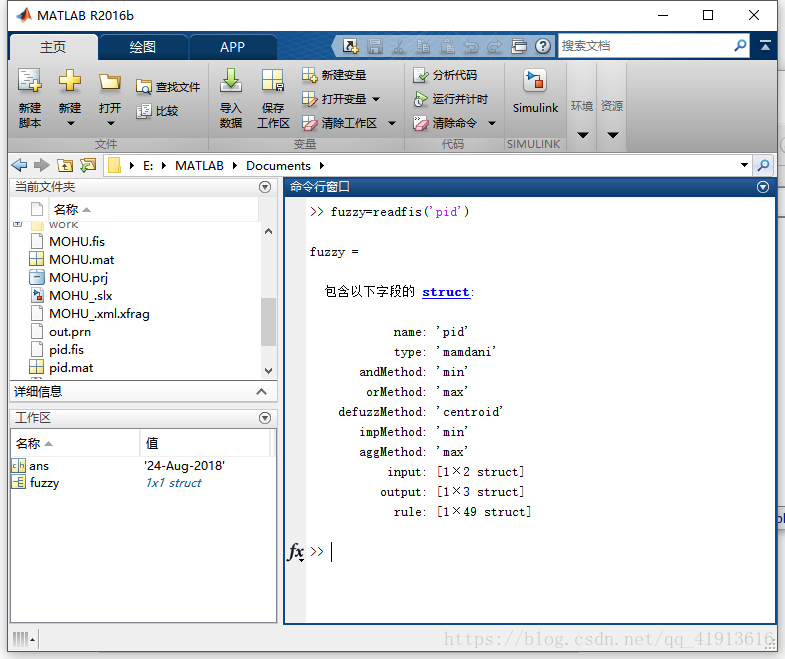
然後在matlab命令列裡把之前儲存的模型讀取出來

用readfis命令把之前儲存的資料賦給變數fuzzy，模型名字你們取得是什麼就寫什麼

之後在模擬fuzzy圖形上雙擊，把引數設成fuzzy，就是上面的步驟

最後就是test了，很坑啊，matlab2016a之後的版本就沒有那個功能了，所以得用下別人的軟體來做最後的測試，之後就看著慢慢設定就好，我只做到了測試執行那一步，因為引數還要調整所以就沒到之後導表

大概就這麼多了，其實都是給新手講的，也想給自己留著複習複習，還有感謝各位在csdn裡留下的各種學習資料，謝謝