影象處理中的傅立葉變換
傅立葉變換在影象處理中有非常重要的作用。因為不僅傅立葉分析涉及影象處理很多方面,傅立 葉改進演算法,比如離散餘弦變換,gabor與小波在影象處理中也有重要的分量。傅立葉變換在影象處理的重要作用:
1.影象增強與影象去噪
絕 大部分噪音都是影象的高頻分量,通過低通濾波器來濾除高頻——噪聲; 邊緣也是影象的高頻分量,可以通過新增高頻分量來增強原始影象的邊緣;
2.影象分割之邊緣檢測
提 取影象高頻分量
3.影象特徵提取:
形狀特徵:傅立葉描述子
紋 理特徵:直接通過傅立葉係數來計算紋理特徵
其他特徵:將提取的特徵值進行傅立葉變 換來使特徵具有平移、伸縮、旋轉不變性
4.影象壓縮
可以直接通過傅立葉係數來壓縮資料;常用的離散餘弦變換是傅立葉變換的實變換;傅立葉變換。
傅立葉變換是將 時域訊號分解為不同頻率的正弦訊號或餘弦函式疊加之和。連續情況下要求原始訊號在一個週期內滿足絕對可積條件。離散情況下,傅立葉變換一定存在。岡薩雷斯 版<影象處理>裡面的解釋非常形象:一個恰當的比喻是將傅立葉變換比作一個玻璃稜鏡。稜鏡是可以將光分解為不同顏色的物理儀器,每個成分的顏 色由波長(或頻率)來決定。傅立葉變換可以看作是數學上的稜鏡,將函式基於頻率分解為不同的成分。當我們考慮光時,討論它的光譜或頻率譜。同樣,傅立葉變 換使我們能通過頻率成分來分析一個函式。
傅立葉變換有很多優良的性質。
如線性, 對稱性(可以用在計算訊號的傅立葉變換裡面);
時移性:函式在時域中的時移,對 應於其在頻率域中附加產生的相移,而幅度頻譜則保持不變;
頻移性:函式在時域中乘 以e^jwt,可以使整個頻譜搬移w。這個也叫調製定理,通訊裡面訊號的頻分複用需要用到這個特性(將不同的訊號調製到不同的頻段上同時傳輸);
卷積定理:時域卷積等於頻域乘積;時域乘積等於頻域卷積(附加一個係數)。(影象處理裡面 這個是個重點)。
訊號在頻率域的表現。
在頻域中,頻率越大說明原始訊號變化速度越快;頻率越小說明原始訊號越平緩。當頻率為0時,表示直 流訊號,沒有變化。因此,頻率的大小反應了訊號的變化快慢。高頻分量解釋訊號的突變部分,而低頻分量決定訊號的整體形象。
在影象處理中,頻域反應了影象在空域灰度變化劇烈程度,也就是影象灰度的變化速度,也就是影象的梯 度大小。對影象而言,影象的邊緣部分是突變部分,變化較快,因此反應在頻域上是高頻分量;影象的噪聲大部分情況下是高頻部分;影象平緩變化部分則為低頻分 量。也就是說,傅立葉變換提供另外一個角度來觀察影象,可以將影象從灰度分佈轉化到頻率分佈上來觀察影象的特徵。書面一點說就是,傅立葉變換提供了一條從 空域到頻率自由轉換的途徑。對影象處理而言,以下概念非常的重要:
影象高頻分量: 影象突變部分;在某些情況下指影象邊緣資訊,某些情況下指噪聲,更多是兩者的混合;
低 頻分量:影象變化平緩的部分,也就是影象輪廓資訊
高通濾波器:讓影象使低頻分量抑 制,高頻分量通過
低通濾波器:與高通相反,讓影象使高頻分量抑制,低頻分量通過
帶通濾波器:使影象在某一部分的頻率資訊通過,其他過低或過高都抑制
帶阻濾波器,是帶通的反。
模板運算與卷積定理
在時域內做模板運算,實際上就是對影象進行卷積。 模板運算是影象處理一個很重要的處理過程,很多影象處理過程,比如增強/去噪(這兩個分不清楚),邊緣檢測中普遍用到。根據卷積定理,時域卷積等價與頻域 乘積。因此,在時域內對影象做模板運算就等效於在頻域內對影象做濾波處理。
比如說 一個均值模板,其頻域響應為一個低通濾波器;在時域內對影象作均值濾波就等效於在頻域內對影象用均值模板的頻域響應對影象的頻域響應作一個低通濾波。
影象去噪
影象去噪 就是壓制影象的噪音部分。因此,如果噪音是高頻額,從頻域的角度來看,就是需要用一個低通濾波器對影象進行處理。通過低通濾波器可以抑制影象的高頻分量。 但是這種情況下常常會造成邊緣資訊的抑制。常見的去噪模板有均值模板,高斯模板等。這兩種濾波器都是在區域性區域抑制影象的高頻分量,模糊影象邊緣的同時也 抑制了噪聲。還有一種非線性濾波-中值濾波器。中值濾波器對脈衝型噪聲有很好的去掉。因為脈衝點都是突變的點,排序以後輸出中值,那麼那些最大點和最小點 就可以去掉了。中值濾波對高斯噪音效果較差。
椒鹽噪聲:對於椒鹽採用中值濾波可以 很好的去除。用均值也可以取得一定的效果,但是會引起邊緣的模糊。
高斯白噪聲:白 噪音在整個頻域的都有分佈,好像比較困難。
岡薩雷斯版影象處理P185:算術均值 濾波器和幾何均值濾波器(尤其是後者)更適合於處理高斯或者均勻的隨機噪聲。諧波均值濾波器更適合於處理脈衝噪聲。
影象增強
有時候感覺影象增 強與影象去噪是一對矛盾的過程,影象增強經常是需要增強影象的邊緣,以獲得更好的顯示效果,這就需要增加影象的高頻分量。而影象去噪是為了消除影象的噪 音,也就是需要抑制高頻分量。有時候這兩個又是指類似的事情。比如說,消除噪音的同時影象的顯示效果顯著的提升了,那麼,這時候就是同樣的意思了。
常見的影象增強方法有對比度拉伸,直方圖均衡化,影象銳化等。前面兩個是在空域進行基於像 素點的變換,後面一個是在頻域處理。我理解的銳化就是直接在影象上加上影象高通濾波後的分量,也就是影象的邊緣效果。對比度拉伸和直方圖均衡化都是為了提 高影象的對比度,也就是使影象看起來差異更明顯一些,我想,經過這樣的處理以後,影象也應該增強了影象的高頻分量,使得影象的細節上差異更大。同時也引入 了一些噪音。
對影象二維傅立葉變換的意義
眾所周至,傅立葉變換可以將連續或離散的函式序列從空域對映到頻域上,因此,傅立葉變換是資訊與訊號學中不可獲缺的強大工具。但是,由於傅立 葉變換在學習時是以一大堆公式的形式給出的,因此很多人(包括我在內)往往在做了一大堆習題掌握了變換的數學表示卻對其變換後的物理意義一無所知,尤其是 自學的時候更是暈頭轉向。
數學公式:
1維的離散序列的DFT變換公式為:

2維的離散矩陣的DFT變換公式為:

1.使用模板處理影象相關概念:
模板:矩陣方塊,其數學含義是一種卷積運算。
卷積運算:可看作是加權求和的過程,使用到的影象區域中的每個畫素分別於卷積核(權矩陣)的每個元素對應相
乘,所有乘積之和作為區域中心畫素的新值。
卷積核:卷積時使用到的權用一個矩陣表示,該矩陣與使用的影象區域大小相同,其行、列都是奇數,
是一個權矩陣。
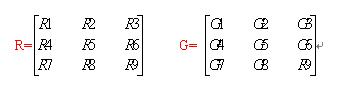
卷積示例:
3 * 3 的畫素區域R與卷積核G的卷積運算:
R5(中心畫素)=R1G1 + R2G2 + R3G3 + R4G4 + R5G5 + R6G6 + R7G7 + R8G8 + R9G9
2.使用模板處理影象的問題:
邊界問題:當處理影象邊界畫素時,卷積核與影象使用區域不能匹配,卷積核的中心與邊界畫素點對應,
卷積運算將出現問題。
處理辦法:
A. 忽略邊界畫素,即處理後的影象將丟掉這些畫素。
B. 保留原邊界畫素,即copy邊界畫素到處理後的影象。
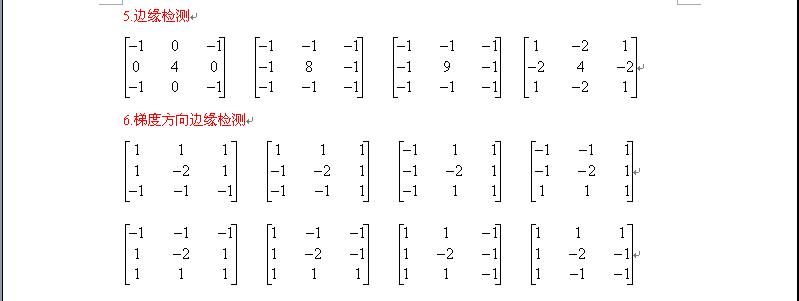
3.常用模板:
例子1.:
//【1】以灰度模式讀取原始影象並顯示
Mat srcImage = imread("1.jpg", 0);
if(!srcImage.data ) { printf("讀取圖片錯誤,請確定目錄下是否有imread函式指定圖片存在~! \n"); return false; }
imshow("原始影象" , srcImage);
//【2】將輸入影象延擴到最佳的尺寸,邊界用0補充
int m = getOptimalDFTSize( srcImage.rows );
int n = getOptimalDFTSize( srcImage.cols );
//將新增的畫素初始化為0.
Mat padded;
copyMakeBorder(srcImage, padded, 0, m - srcImage.rows, 0, n - srcImage.cols, BORDER_CONSTANT, Scalar::all(0));
//【3】為傅立葉變換的結果(實部和虛部)分配儲存空間。
//將planes陣列組合合併成一個多通道的陣列complexI
Mat planes[] = {Mat_<float>(padded), Mat::zeros(padded.size(), CV_32F)};
Mat complexI;
merge(planes, 2, complexI);
//【4】進行就地離散傅立葉變換
dft(complexI, complexI);
//【5】將複數轉換為幅值,即=> log(1 + sqrt(Re(DFT(I))^2 + Im(DFT(I))^2))
split(complexI, planes); // 將多通道陣列complexI分離成幾個單通道陣列,planes[0] = Re(DFT(I), planes[1] = Im(DFT(I))
magnitude(planes[0], planes[1], planes[0]);// planes[0] = magnitude
Mat magnitudeImage = planes[0];
//【6】進行對數尺度(logarithmic scale)縮放
magnitudeImage += Scalar::all(1);
log(magnitudeImage, magnitudeImage);//求自然對數
//【7】剪下和重分佈幅度圖象限
//若有奇數行或奇數列,進行頻譜裁剪
magnitudeImage = magnitudeImage(Rect(0, 0, magnitudeImage.cols & -2, magnitudeImage.rows & -2));
//重新排列傅立葉影象中的象限,使得原點位於影象中心
int cx = magnitudeImage.cols/2;
int cy = magnitudeImage.rows/2;
Mat q0(magnitudeImage, Rect(0, 0, cx, cy)); // ROI區域的左上
Mat q1(magnitudeImage, Rect(cx, 0, cx, cy)); // ROI區域的右上
Mat q2(magnitudeImage, Rect(0, cy, cx, cy)); // ROI區域的左下
Mat q3(magnitudeImage, Rect(cx, cy, cx, cy)); // ROI區域的右下
//交換象限(左上與右下進行交換)
Mat tmp;
q0.copyTo(tmp);
q3.copyTo(q0);
tmp.copyTo(q3);
//交換象限(右上與左下進行交換)
q1.copyTo(tmp);
q2.copyTo(q1);
tmp.copyTo(q2);
//【8】歸一化,用0到1之間的浮點值將矩陣變換為可視的影象格式
//此句程式碼的OpenCV2版為:
//normalize(magnitudeImage, magnitudeImage, 0, 1, CV_MINMAX);
//此句程式碼的OpenCV3版為:
normalize(magnitudeImage, magnitudeImage, 0, 1, NORM_MINMAX);
//【9】顯示效果圖
imshow("頻譜幅值", magnitudeImage); 函式解讀:
C++: intgetOptimalDFTSize(int vecsize)
原始碼解讀;
copyMakeBorder
C++: void copyMakeBorder(InputArraysrc, OutputArray dst, int top, int bottom, int left,int right, intborderType, const Scalar& value=Scalar())
src: 源影象
dst: 目標影象,和源影象有相同的型別,dst.cols=src.cols+left+right; dst.rows=src.rows+dst.top+dst.bottom
top:
bottom:
left:
right: 以上四個引數指定了在src影象周圍附加的畫素個數。
borderType: 邊框型別
value: 當borderType==BORDER_CONSTANT時需要指定該值。
例子2. [cpp] view plain copy print?
- int cv::getOptimalDFTSize( int size0 )
- {
- int a = 0, b = sizeof(optimalDFTSizeTab)/sizeof(optimalDFTSizeTab[0]) -1;
- if( (unsigned)size0 >= (unsigned)optimalDFTSizeTab[b] )
- return -1;
- while( a < b )//二分查詢合適的size
- {
- int c = (a + b) >> 1;
- if( size0 <= optimalDFTSizeTab[c] )
- b = c;
- else
- a = c+1;
- }
- returnoptimalDFTSizeTab[b];
- }</span>
optimalDFTSizeTab定義在namespace cv中,裡邊的數值為2^x*3^y*5^z
static const int optimalDFTSizeTab[] = {1,2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16,…, 2123366400, 2125764000};
示例程式碼:
[cpp] view plain copy print?- <span style="font-size:18px;">#include <opencv2/core/core.hpp>
- #include<opencv2/highgui/highgui.hpp>
- #include<opencv2/imgproc/imgproc.hpp>
- #include <iostream>
- usingnamespace cv;
- usingnamespace std;
- int main(){
- Matsrc = imread("fruits.jpg");
- if(src.empty())
- {
- return-1;
- }
- Matsrc_gray;
- cvtColor(src,src_gray,CV_RGB2GRAY);//灰度影象做傅立葉變換
- intm = getOptimalDFTSize(src_gray.rows);//2,3,5的倍數有更高效率的傅立葉轉換
- intn = getOptimalDFTSize(src_gray.cols);
- Matdst;
- ///把灰度影象放在左上角,在右邊和下邊擴充套件影象,擴充套件部分填充為0;
- copyMakeBorder(src_gray,dst,0,m-src_gray.rows,0,n-src_gray.cols,BORDER_CONSTANT,Scalar::all(0));
- cout<<dst.size()<<endl;
- //新建一個兩頁的array,其中第一頁用擴充套件後的影象初始化,第二頁初始化為0
- Matplanes[] = {Mat_<float>(dst), Mat::zeros(dst.size(), CV_32F)};
- Mat completeI;
- merge(planes,2,completeI);//把兩頁合成一個2通道的mat
- //對上邊合成的mat進行傅立葉變換,支援原地操作,傅立葉變換結果為複數。通道1存的是實部,通道2存的是虛部。
- dft(completeI,completeI);
- split(completeI,planes);//把變換後的結果分割到各個陣列的兩頁中,方便後續操作
- magnitude(planes[0],planes[1],planes[0]);//求傅立葉變換各頻率的幅值,幅值放在第一頁中。
- MatmagI = planes[0];
- //傅立葉變換的幅度值範圍大到不適合在螢幕上顯示。高值在螢幕上顯示為白點,
- //而低值為黑點,高低值的變化無法有效分辨。為了在螢幕上凸顯出高低變化的連續性,我們可以用對數尺度來替換線性尺度:
- magI+= 1;
- log(magI,magI);//取對數
- magI= magI(Rect(0,0,src_gray.cols,src_gray.rows));//前邊對原始影象進行了擴充套件,這裡把對原始影象傅立葉變換取出,剔除擴充套件部分。
- //這一步的目的仍然是為了顯示。 現在我們有了重分佈後的幅度圖,
- //但是幅度值仍然超過可顯示範圍[0,1] 。我們使用 normalize() 函式將幅度歸一化到可顯示範圍。
- normalize(magI,magI,0,1,CV_MINMAX);//傅立葉影象進行歸一化。
- //重新分配象限,使(0,0)移動到影象中心,
- //在《數字影象處理》中,傅立葉變換之前要對源影象乘以(-1)^(x+y)進行中心化。
- //這是是對傅立葉變換結果進行中心化
- intcx = magI.cols/2;
- intcy = magI.rows/2;
- Mattmp;
- Matq0(magI,Rect(0,0,cx,cy));
- Matq1(magI,Rect(cx,0,cx,cy));
-
相關推薦
影象處理中傅立葉變換以及頻率域影象增強詳解
岡薩雷斯版<影象處理>裡面的解釋非常形象:一個恰當的比喻是將傅立葉變換比作一個玻璃稜鏡。稜鏡是可以將光分解為不同顏色的物理儀器,每個成分的顏色由波長(或頻率)來決定。傅立葉變換可以看作是數學上的稜鏡,將函式基於頻率分解為不同的成分。當我們考慮光時,討論它的光譜
影象處理-離散傅立葉變換-數字影象處理第三版第四章內容
影象傅立葉變換方法有很多,可以通過空間光調製器輸入影象後在通過平行光照明經過傅立葉變換透鏡進行傅立葉變換,另一個方法就是利用計算機進行傅立葉變換,其中傅立葉變換有兩種演算法一種是DFT還有一種是FFT(快速傅立葉變換)。 首先我介紹一下影象的定義,影象是怎麼去得到的
數字影象處理-離散傅立葉變換(opencv3+C++顯示)
參考: http://daily.zhihu.com/story/3935067 http://blog.csdn.net/keith_bb/article/details/53389819 在學習訊號與系統或通訊原理等課程裡面可能對傅立葉變換有了一定的瞭解。我們知道傅立葉變換是把一個訊號從時域變換
數字影象處理,讀懂頻域處理的“傅立葉變換”
轉載自:https://blog.csdn.net/ebowtang/article/details/39004979 以下部分文字資料整合於網路,本文僅供自己學習用! 這是一幅很絕的一維傅立葉變換動態圖 一,讀懂傅立葉變換 一個訊號能表示成傅立葉級數
頻域處理:傅立葉變換及小波變換
頻域處理:傅立葉變換及小波變換 引言 1、傅立葉變換 2、小波變換 3、程式 引言 影象處理–>頻域處理–>傅立葉變換、小波變換。用另一種方法來觀察世界的話,你會發現世界是永恆不變的。
opencv 中 傅立葉變換 FFT
分享一下我老師大神的人工智慧教程!零基礎,通俗易懂!http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識,造福人民,實現我們中華民族偉大復興!
對影象二維傅立葉變換的意義
眾所周至,傅立葉變換可以將連續或離散的函式序列從空域對映到頻域上,因此,傅立葉變換是資訊與訊號學中不可獲缺的強大工具。但是,由於傅立葉變換在學習時是以一大堆公式的形式給出的,因此很多人(包括我在內)往往在做了一大堆習題掌握了變換的數學表示卻對其變換後的物理意義
影象的離散傅立葉變換
close all, clear, clc warning off all img_w = 640; img_h = img_w; xOfCenter = img_w / 2; yOfCenter = img_h / 2; %% DFT of oblique rectang
訊號處理、傅立葉變換 、小波變換的入門資料
以下摘錄來自“王昱博,訊號處理博士僧”的回答 在傅立葉變換中,如果一個訊號在實數域滿足勒貝格可度量條件(Lebesgue-measurable)則這個訊號的傅立葉變換收斂。通過傅立葉變換我們可以看到的是訊號的時域特徵被完全的變換到了頻率域。這時在時域中不明顯的週期性變化被直觀的反應到了對應的頻率域。數學上
離散傅立葉變換在影象處理中的應用_學習
1、為什麼要進行傅立葉變換,其物理意義是什麼? 傅立葉原理表明:任何連續測量的時序或訊號,都可以表示為不同頻率的正弦波訊號的無限疊加。而根據該原理創立的傅立葉變換演算法利用直接測量到的原始訊號,以累加方式來計算該訊號中不同正弦波訊號的頻率、振幅和相位。 和傅立葉
影象處理:如何理解傅立葉變換在影象處理中的應用
宣告: 這篇文章的主要目的是通過建立一維傅立葉變換與影象傅立葉變換中相關概念的對應關係來幫助讀者理解影象處理中的離散傅立葉變換,因此,理解影象中離散傅立葉變換的前提條件是讀者需要了解一維傅立葉變換的基本知識,詳情可參考:https://zhuan
傅立葉變換在影象處理中的應用
傅立葉變換在影象處理中有非常非常的作用。因為不僅傅立葉分析涉及影象處理的很多方面,傅立葉的改進演算法, 比如離散餘弦變換,gabor與小波在影象處理中也有重要的分量。 印象中,傅立葉變換在影象處理以下幾個話題都有重要作用:1.影象增強與影象去噪 絕大部分噪音都是影象的高頻分
數字影象處理學習筆記(1)——傅立葉變換在影象處理中的應用
1.理解二維傅立葉變換的定義 1.1二維傅立葉變換 二維Fourier變換: 逆變換: 1.2二維離散傅立葉變換 一個影象尺寸為M×N的 函式的離散傅立葉變換由以下等式給出: 其中 和。其中變數u和v用於確定它們的頻率,頻域系統是由所張成的座標系,其
影象處理中的傅立葉變換
傅立葉變換在影象處理中有非常重要的作用。因為不僅傅立葉分析涉及影象處理很多方面,傅立 葉改進演算法,比如離散餘弦變換,gabor與小波在影象處理中也有重要的分量。傅立葉變換在
傅立葉變換在影象處理中的作用
傅立葉變換在影象處理中非常的有用。因為不僅傅立葉分析涉及影象處理的很多方面,傅立葉的改進演算法, 比如離散餘弦變換,gabor與小波在影象處理中也有重要的分量。 印象中,傅立葉變換在影象處理以下幾個話題都有重要作用: 1.影象增強與影象去噪 絕大部分噪音都是影象的高頻
影象處理中的數學原理詳解(Part8) ——傅立葉變換的來龍去脈
全文目錄請見http://blog.csdn.net/baimafujinji/article/details/48467225千呼萬喚始出來,我們前面已經做了很多很多的準備,終於可以揭開傅立葉變換的面
c語言數字影象處理(六):二維離散傅立葉變換
基礎知識 複數表示 C = R + jI 極座標:C = |C|(cosθ + jsinθ) 尤拉公式:C = |C|ejθ 有關更多的時域與複頻域的知識可以學習複變函式與積分變換,本篇文章只給出DFT公式,性質,以及實現方法 二維離散傅立葉變換(DFT) 其中f(x,y)為原影象,F(u,
快速傅立葉變換在訊號處理中的應用
傅立葉變換FT(Fourier Transform)是一種將訊號從時域變換到頻域的變換形式。它在聲學、訊號處理等領域有廣泛的應用。計算機處理訊號的要求是:在時域和頻域都應該是離散的,而且都應該是有限長的。而傅立葉變換僅能處理連續訊號,離散傅立葉變換DFT(Discrete F
傅立葉變換及其在opencv中影象去噪的實現
前言 我保證這篇文章和你以前看過的所有文章都不同,這是12年還在果殼的時候寫的,但是當時沒有來得及寫 完就出國了……於是拖了兩年,嗯,我是拖延症患者…… 這篇文章的核心思想就是: 要讓讀者在不看任何數學公式的情況下理解傅立葉分析。 傅立葉分析不僅僅是一個數學工
OpenCV中對影象進行二維離散傅立葉變換
#include<opencv2/opencv.hpp> #include <highgui.h> #include <iostream> #include <cv.h> #include <opencv2/core/c