前置技能樹

1.兩個N階矩陣相乘：複雜度為N^3，（能優化到更低，但沒必要去掌握）
2.快速冪演算法：求數a^t，能在 （log t）的複雜度下，得解
3.矩陣快速冪：把矩陣A^k，跟上一個思路一樣，不過基礎單元a\*a變成了A\*A，複雜度就是矩陣\*快速冪(N^3\* long k)
4.求餘運算：（a+b）%c=(a%c+b%c)%c，形狀如此。乘法，次方也行

型別1：根據矩陣快速冪的定義操作

一： 給定矩陣A，請快速計算出A^n（n個A相乘）的結果，輸出的每個數都mod p。

這是裸的矩陣快速冪，點亮前置技能樹就能搞。

二：給定 NxN 矩陣 A，正整數 K，正整數 M，求 S = A^1 + A^2 + … + A^K。輸出時每個元素要 mod M。

網上有兩種思路，
1.採用二分的方式：

首先我們知道，A^i可以二分求出。然後我們需要對整個題目的資料規模k進行二分。比如，當k=6時，有：
A + A^2 + A^3 + A^4 + A^5 + A^6 =(A + A^2 + A^3) + A^3*(A + A^2 + A^3)
應用這個式子後，規模k減小了一半。我們二分求出A^3後再遞迴地計算A + A^2 + A^3，即可得到原問題的答案。

矩陣構造完成後，從N\*N變為2N\*2N，空間無壓力
不想進原文的可以看這張圖：

型別2：對每個點同時操作，求k次後的個點情況

一：給定n個點，m個操作，構造O(m+n)的演算法輸出m個操作後各點的位置。操作有平移、縮放、翻轉和旋轉

這裡的操作是對所有點同時進行的。其中翻轉是以座標軸為對稱軸進行翻轉（兩種情況），旋轉則以原點為中心。

分析：如果對每個點分別進行模擬，那麼m個操作總共耗時O(mn)。
利用矩陣乘法可以在O(m)的時間裡把所有操作合併為一個矩陣，然後每個點與該矩陣相乘即可直接得出最終該點的位置，總共耗時O(m+n)。
假設初始時某個點的座標為x和y，下面5個矩陣可以分別對其進行平移、旋轉、翻轉和旋轉操作。
預先把所有m個操作所對應的矩陣全部乘起來，再乘以(x,y,1)，即可一步得出最終點的位置。

二：VOJ1049 題目大意：順次給出m個置換，反覆使用這m個置換對初始序列進行操作，問k次置換後的序列。m<=10, k<2^31。

 因為是順次置換，可以知道每m次一個迴圈，將這m個置換“合併”起來（算出這m個置換的乘積），然後接下來我們需要執行這個置換k/m次（取整，若有餘數則剩下幾步模擬即可）。
 注意任意一個置換都可以表示成矩陣的形式。例如，將1 2 3 4置換為3 1 2 4，相當於下面的矩陣乘法：

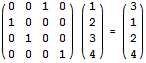
型別3： 點A到B的方案數

1.給定一個有向圖，問從A點恰好走k步（允許重複經過邊）到達B點的方案數mod p的值

分析：
如果不能重複經過邊，直接暴力搜尋就行了，每條邊訪問一次，複雜度為 O(E)。能重複的話，只能通過k來搜尋，這類題k極大，複雜度就很高了。

我們考慮DP,令f(i,j,z)為從i走z步到達j的方案數，那麼有

觀察形式，發現可以消去z這一維，即：

沒錯，就是個矩陣乘法，求A^k。

我們得到一個重要結論：無論圖怎樣變化，求從某一點走到另一個點的確定邊數的路徑數，只需將每個時刻的圖鄰接矩陣直接乘起來就得到了答案矩陣。

2.給定一個有向圖，問從A點k步內（允許重複經過邊）到達B點的方案數mod p的值

這裡是k步內，那麼就是說求：S = A + A^2 + A^3 + ... + A^k
根據前面的型別一的2，就可以完成了。
注意：
1.到n點後就停止（一般都會這樣），將A(n,i~n)置為0。

ps:這裡有個神奇的東西，上面那句做完後，將A(n,n)置為1，記為A',最後的矩陣裡
（A'^k）[1][n]==S[1][n]
A(n,n)=1可以理解為，到n點就不走了。用矩陣乘法也可以看出來。

型別4 構造矩陣求解線性遞推關係

構造矩陣呢，所謂規律其實不好用，可以參照“型別1 的二.2”和本類的3，根據邏輯來建立。

1.給定n和p，求第n個Fibonacci數mod p的值，n不超過2^31

根據前面的一些思路，現在我們需要構造一個2 x 2的矩陣，使得它乘以(a,b)得到的結果是(b,a+b)

即是：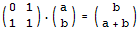

2.VOJ 1067 求f(n) = 4f(n-1) – 3f(n-2) + 2f(n-4)

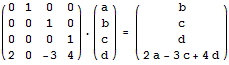
3.HDU 5895 (擷取題中的矩陣構造部分)
f(n)=2×f(n−1)+f(n−2),f(1)=1,f(0)=0，求：g(n)=f(1)^2+f(2)^2+···+f(n)^2

利用邏輯遞推來構造
首先寫g(n)的遞推公式，利用公式構建下圖右邊的矩陣等式。

根據矩陣等式右邊的模型，補全左邊

因為要滿足遞推的要求，將f(n)^2,f(n)f(n-1)求其遞推式，根據遞推式補全A矩陣，如下面兩圖
（ps:這裡如果出現新元素，要加到矩陣等式的右邊，再重複補全左邊，直到不再出現新元素。如果一直迴圈，那應該是做錯了）

型別5 修改矩陣乘法的定義

具體見：IOI國家集訓隊2008 俞華程《矩陣乘法在資訊學中的應用》3.2；3.3；
1.USACO’NOV07
給定一張M條邊的無向帶權圖，求從起點S到終點E恰好經過K條邊的最短路徑。2 ≤ M ≤ 100, 2 ≤ K ≤ 1000000。保證每個連邊的點度至少為2。

這個問題和前面講的求兩點間恰好經過K條邊的路徑數非常相似。於是，我們也希望能夠找到一個類似的矩陣乘法的方法。
這裡我們可以修改矩陣的 ‘乘法’函式的定義，
原來是：C[i][j] =  求和：{k:從1到n}  (A[i][k]*B[k,j])
現在是：C[i][j] =  求最小項：{k:從1到n} (A[i][k]+B[k,j])
現在我們就可以用快速冪求解了。
再來看這道題的解法，其實基本模型是floyd演算法求最短路。

2.給定一張有向圖，求某兩點間通過邊數恰好為K的路徑，使得最大邊最小。

這裡我們修改‘乘法’定義為：
C[i][j] =  求最小項：{k:從1到n} max(A[i][k],B[k,j])

3. 最小最小邊問題：給定一張有向圖，求邊數恰好為K的路徑上最小邊最小是多少。

這裡我們修改‘乘法’定義為：
C[i][j] =  求最小項：{k:從1到n} min(A[i][k],B[k,j])

4.給定一張有向圖，求邊數不超過K的路徑上最大邊最小是多少。

即為，可以在點上停留，修改A[i][i]=-inf，就可以了。

給定一張有向圖，求邊數在範圍K1到K2的路徑上最大邊最小是多少。(這個純搬運了)

儘管區間還是可以轉化為兩個區間的差。但是取最小值操作無法進行做逆運算，換句話說就是知道[0, K2] , [0, K1 − 1]的答案後無法求出[K1, K2]。
我們重新看拓展2，增加一條i到i的權為−∞的邊，等價於將圖矩陣的主對角線上的值都變成−∞。
從另一個方面來考慮，可以說是把前一個答案儲存下來了，因為根據修改過的矩陣乘法的定義：
當k = j時，max {A [i, k] , G [k, j]} = A [i, j]。
即原來的答案，而其他項運算出來的結果就是新的答案。設原矩陣為G0，可以先乘K1個G0，然後再乘K2 − K1個可以儲存答案的G，答案也就G0^K1*G^(K2−K1)。
直接使用快速冪，時間複雜度為O(N^3 log K2)。

總結：對DP的優化

其實仔細分析的話，前面幾個型別都是DP或者遞推，但由於複雜度的問題，採取了矩陣的優化
這類DP本來的複雜度一般是n^2*k，不一定用了矩陣後複雜度會降低，畢竟矩陣的乘法是n^3的操作。
但對於一些題，由於k賊大比如1e8什麼的，n較小(N<100)，必須優化。
而矩陣優化過後是n^3*(long k)，就能搞了。

來看俞華程的總結

如果一個動態規劃方程能夠用矩陣乘法來進行優化，那麼必須滿足：
1. 狀態必須是一維或者兩維，如果狀態本身有超過兩維，可以通過把多維狀態壓縮到一維的方法降到兩維（此時狀態數並沒有變化）。
2. 每一個狀態f [i] [j]必須滿足只和f [i − 1] [k]有關，並且只能是線性關係
3. 滿足前兩條的情況下，可以使用矩陣乘法，但是可能並不能達到優化複雜度的目的。
如果對於不同的i，轉移矩陣沒有規律，那麼是無法使用快速冪來加速矩陣乘法的。通常情況下，都有轉移矩陣都相同或者至少是迴圈出現。

1.經典題目9 用1 x 2的多米諾骨牌填滿M x N的矩形有多少種方案，M<=5，N<2^31，輸出答案mod p的結果

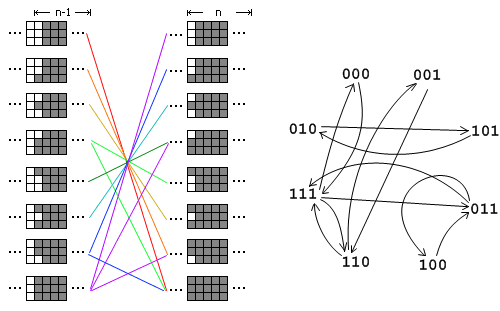
大牛的圖很清晰了，根據上圖右邊的狀態轉移式建邊，形成的矩陣就是我們所需要的A矩陣。再用快速冪求解。