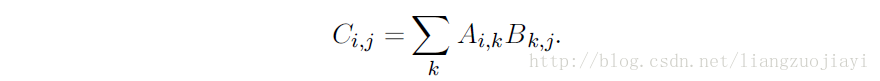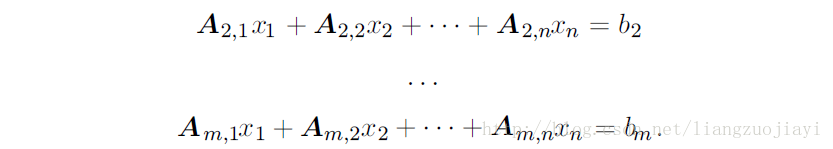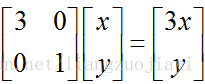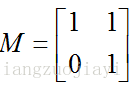參考了《深度學習》鉅作，以下是矩陣篇的目錄。

1 矩陣的乘法

設矩陣A為m×n矩陣，B為n×p矩陣，則它們的乘法公式為：

相關程式碼實現：

# 矩陣滴乘法運算
# 注意：需要傳入np.matrix型別資料
def Matrix_Mul(a,b):
    if a.shape[1] != b.shape[0]:
        print('這兩個矩陣無法做乘法，請檢查左邊矩陣的列數是否與右邊矩陣的行數相等！')
    else:
        c = np.zeros(a.shape[0]*b.shape[1]).reshape(a.shape[0],b.shape[1])
        for
 
 i in range(a.shape[0]):
            for j in range(b.shape[1]):
                for k in range(a.shape[1]):
                    c[i,j] = c[i,j] + a[i,k]*b[k,j]
    return c

import numpy as np
a = np.matrix([[2,3,4],[1,0,5]])
b = np.matrix([1,0,1]).T
Matrix_Mul(a=a,b=b)

輸出結果：

當然，你可以直接用a*b計算出來一樣的結果，我這裡只是為了單純的自己實現一下矩陣的乘法運算。

2 矩陣與向量乘法運算的三種等價寫法

第一種

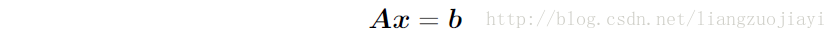
第二種

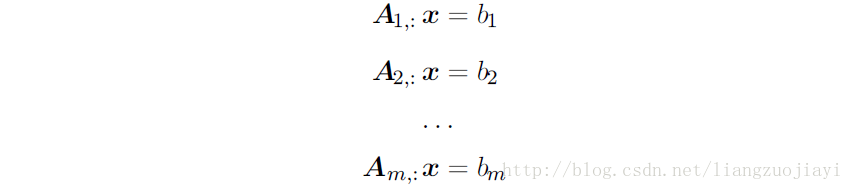
第三種

3、矩陣乘法的理解

矩陣乘法對應了一個變換，是把任意一個向量變成另一個方向或長度的新向量。在這個變化過程中，原向量主要發生旋轉、伸縮的變化。如果矩陣對某些向量只發生伸縮變換，不產生旋轉效果，那麼這些向量就稱為這個矩陣的特徵向量，伸縮的比例就是特徵值。

比如M矩陣變換：

它對應的線性變換是下面的形式形式：

那麼如果矩陣M不是對稱的，比如

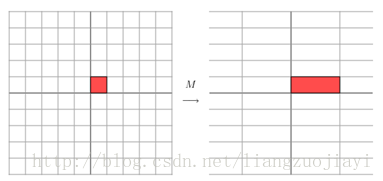
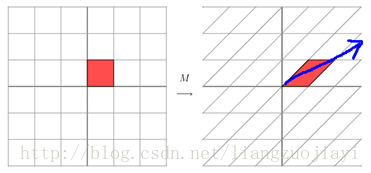
它所描述的變換如下圖所示：

這其實是在平面上對一個軸進行的拉伸變換【如藍色箭頭所示】，在圖中藍色箭頭是一個最主要的變化方向。變化方向可能有不止一個，但如果我們想要描述好一個變換，那我們就描述好這個變換主要的變化方向就好了。