現如今智慧啟發式演算法很普遍，用處也很多，遺傳演算法、模擬退火、蟻群演算法、粒子群演算法等都是常用的幾個智慧演算法，借用之前做的數模題目的例子，大致記錄一下遺傳演算法的Matlab實現。

題目具體分析就不闡述了，核心要求是給出由理想起始點倒車入庫的泊車策略，包括車速、前輪轉角、後輪行駛距離。

假設我現在已經得到了一個比較好的倒車起始點，且在最終到達車庫門前的過程中方向盤不動。遺傳演算法求解過程：

由於該模型方程較複雜且約束條件為非線性的，直接用求解面臨這許多困難，故考慮用啟發式演算法中常用的遺傳演算法求解。遺傳演算法不需要給出優化變數的初始值，只需要給出優化變數的範圍就可以進行高效並行的全域性搜尋。並且遺傳演算法不需要目標函式的導數梯度等資訊，按照適應度的值就可以進行搜尋最優值。本文研究的泊車問題無法給出的優化引數的初始值，僅能給出優化變數的範圍，並且無法提供目標函式的梯度資訊，所以採用遺傳演算法進行引數優化。

垂直泊車的遺傳演算法優化過程如下：

第一步：確定轉彎半徑範圍

當停車點確定後，由於前輪轉向角不同使得開出的路徑不一樣，但由於角度不直觀且不方便運算，根據阿克曼模型，使用對應的轉彎半徑 作為決策變數。對於小型車，其最大轉向角一般為33.5-39.6°之間，取轉向角為36°，從而確定了轉彎半徑要大於3785mm。

第二步：產生初始種群並編碼

決策變數 為一定區間內的浮點數，不宜採用二進位制編碼，由於 為一定範圍內的浮點數，所以採用實數編碼效果更好。具體做法是在 的取值範圍內，隨機選擇 個染色體，作為初始種群。

第三步：等效距離的選擇與計算^[

為了求解最優的路徑，我們把從理想倒車點到停車位置處所經過的距離的計算式作為適應度函式，算出的適應度稱為等效距離。在產生種群的過程中，難免會得出一些不滿足約束條件的解。工程中常用懲罰策略來解決遺傳演算法中具有非線性約束的問題，懲罰策略的本質是通過懲罰不可行解，將有約束的問題轉化為無約束的問題，即通過增加懲罰項來改變適應度。帶有懲罰項的適應度函式有兩種。

在加法形式下的適應度函式中，本文將懲罰項定義為一很大的常數 ，以此排除不滿足約束條件的值，則適應度函式為：

第四步：對個體進行選擇

採用轉盤演算法對染色體進行選擇，按如下公式計算出種群中每個染色體被選中的概率：

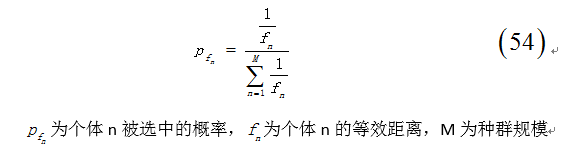
輪盤每轉動一次選中一個個體，若個體的等效距離越小，則被選中的概率越大，由此選中那些路徑較小的個體，使得種群的平均路徑長度不斷減小。

第五步：交叉操作

首先選取對應的交叉概率 。選取交叉概率為0.7， 的值太大，群體更新的速度太快，高適應度的個體很快被破壞。而 的值太小則可能導致搜尋阻滯。隨機選取兩個個體 和 ，交叉公式為：

第六步：變異操作

變異的基因多少是按照變異率 決定的，變異率 很低難以增加種群的多樣性， 太高GA 的搜尋就變成了隨機搜尋，因此，一般取 =0.001~0.1。本文取 =0.01。

第七步：進化終止

進化的終止條件是進化代數到達最大值，進化代數的選擇視具體情況而定，一般取T=100-500，經過重複多次試驗，本文取100。

結果的分析

輸入座標對模型進行測試，一般的，倒車方式為直接倒行時，輸入變數為理想起始點的座標。當倒車方式為兩段式垂直泊車時，需要再新增一個車身與水平線夾角的變數 。

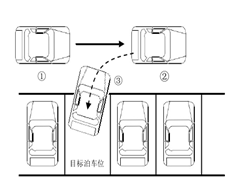
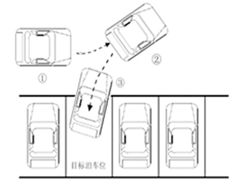
               a.直接倒行                                        b.兩段式

執行程式，開始時輸入倒車起始點，但基於理想起始點的約束，不是任意的點都可以得出解的，比如某些死角點不可能直接倒進車庫中，或者不同的理想點對應不同的倒車方式，所以在分析大量實驗資料後，我們大致給出了輸入座標的範圍。

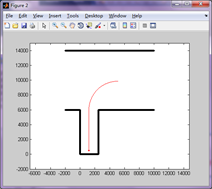
給出程式執行過程中，各代的平均值和最佳值曲線。由曲線可以看出，遺傳演算法收斂程度高，每一代種群平均等效距離的下降速度快，且得出最優路徑時間快，完全保持在100代以內達到最優結果。

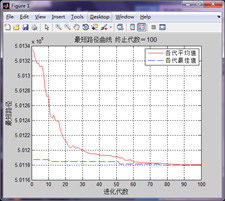
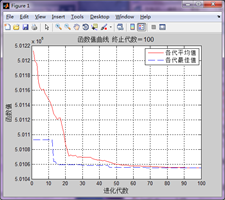
a.直接倒行                                                                       b.兩段式

程式執行完畢後，給出最優的路徑，並在命令視窗顯示出題目需要的幾個引數的具體值，並畫出最優路徑^[9]。

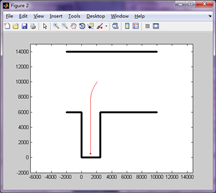
a.直接倒行                                                                     b.兩段式

圖13 最優路徑顯示

論文下載，想要了解的朋友可以看看，水平有限，請勿噴=。=