基於遺傳演算法求解車輛路徑問題
今天整理了一下以前寫過的一個遺傳演算法求解車輛路徑問題的程式(C#寫的),發上來和大家分享一下,有誤的地方還請各位指點。
1、車輛路徑問題:
車輛路徑問題可以描述為:在一個存在供求關係的系統中,有若干臺車輛、若干個配送中心和客戶,要求合理安排車輛的行車路線和出行時間,從而在給定的約束條件下,把客戶需求的貨物從配送中心送到客戶,把客戶供應的貨物從客戶取到配送中心,並使目標函式取得優化。本文以最簡單的無時限單向配送車輛路徑問題為例。
1.1、問題描述:
無時限單向配送車輛路徑問題,是指在制定配送路線時不考慮客戶對貨物送到(或取走)時間要求的純送貨(或純取貨)車輛排程問題。無時限單向配送車輛路徑問題可以描述為:從某配送中心用多臺配送車輛向多個客戶送貨,每個客戶的位置和需求量一定,每臺配送車輛的載重量一定,其一次配送的最大行駛距離一定,要求合理安排車輛配送路線,使目標函式得到優化,並滿足以下條件:
①每條配送路徑上各客戶的需求量之和不超過配送車輛的載重量;
②每條配送路徑的長度不超過配送車輛一次配送的最大行駛距離:
③每個客戶的需求必須滿足,且只能由一臺配送車輛送貨。
1.2、問題模型:
設配送中心有Κ臺配送車輛,每臺車輛的載重量為Qk,其一次配送的最大行駛距離為Dk,需要向L個客戶送貨,每個客戶的貨物需求量為qi,客戶i到j的運距為dij,配送中心到各客戶的距離為d0j,再設 為第k臺車輛配送的客戶數(nk=O表示未使用第k臺車輛),用集合Rk表示第k條路徑,其中的元素Rki表示客戶Rki在路徑k中的順序為i(不包括配送中心),令rk0=0表示配送中心,若以配送總里程最短為目標函式,則可建立如下無時限單向配送車輛路徑問題的數學模型:
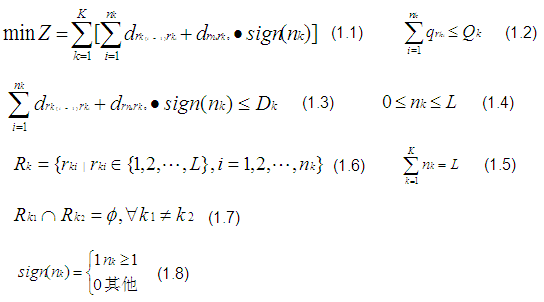
上述模型中,式(1.1)為目標函式,即要求配送總里程(即各條配送路徑的長度之和)最短;式(1.2)保證每條路徑上各客戶的貨物需求量之和不超過配送車輛的載重量;式(1.3)保證每條配送路徑的長度不超過配送車輛一次配送的最大行駛距離;式(1.4)表明每條路徑上的客戶數不超過總客戶數;式(1.5)表明每個客戶都得到配送服務;式(1.6)表示每條路徑的客戶的組成;式(1.7)限制每個客戶僅能有一臺配送車輛送貨;式(1.8)表示當第k輛車服務的客戶數≥1時,說明該臺車參加了配送,則取sign(nk)=1,當第k輛車服務的客戶數< 1時,,表示未使用該臺車輛,則取sign(nk)=0。
2、遺傳演算法:
2.1、遺傳演算法的實施步驟:
遺傳火演算法的實施步驟如下(以目標函式求最小為例)。
第一步:初始化 t←0進化代數計數器;T是最大進化代數;隨機生成M個個體作為初始群體P(t);
第二步:個體評價 計算P(t)中各個個體的適應度;
第三步:選擇運算 將選擇運算元作用於群體;
第四步:交叉運算 將交叉運算元作用於群體;
第五步:變異運算 將變異運算元作用於群體,並通過以上運算得到下一代群體P(t + 1);
第六步:終止條件判斷 t≦T:t← t+1 轉到步驟2;t>T:終止 輸出解。
2.2、遺傳演算法應用步驟:
1)確定決策變數及各種約束條件,即個體的表現型X和問題的解空間;
2)建立優化模型 (目標函式最大OR 最小) 數學描述形式 量化方法;
3)染色體編碼方法;
4)解碼方法;
5)個體適應度的量化評價方法 F(x)
6)設計遺傳運算元;
7)確定有關執行引數。
3、遺傳演算法求解車輛路徑問題:
用遺傳演算法求解配送車輛路徑問題時,確定解的表示和解的評價方法是一項非常關鍵的基礎工作,因為它將直接決定演算法實現的難易程度和演算法效能的優劣。
3.1、解的表示:
客戶直接排列的表示方法,這種表示方法是直接產生L個1~L間的互不重複的自然數的排列,該客戶排列就構成一個解,並對應一種配送路徑方案。按照無時限單向配送車輛優化排程問題的約束條件,可依次將解的元素(客戶)劃入各臺車輛的配送路徑中。例如,對於一個用3臺車輛向9個客戶送貨的配送車輛優化排程問題,設某解中的客戶排列為412876935,可用如下方法得到其對應的配送路徑方案:首先將客戶4(解中的第1個客戶)作為第1臺配送車輛月艮務的第1個客戶,然後判斷能否滿足問題的約束條件,即客戶4的需求量是否超過第1臺車輛的最大載重量,且路徑0-4-0的總長度是否超過第1臺車輛一次配送的最大行駛距離,設能夠滿足,這時可將客戶1(解中的第2個客戶)作為第1臺配送車輛服務的第2個客戶,然後判斷能否滿足問題的約束條件,即客戶4和1的需求量之和是否超過第1臺配送車輛的最大載重量,且路徑0-4-1-0的總長度是否超過第1臺車輛一次配送的最大行駛距離,設仍能滿足,這時可將客戶2(解中的第3個客戶)作為第1臺配送車輛服務的第3個客戶,然後判斷能否滿足問題的約束條件,設仍能滿足,這時可將客戶8作為第1臺配送車輛服務的第4個客戶,設此時不能滿足問題的約束條件,這說明客戶8不能由第1臺配送車輛服務,由此可得第1臺車輛的配送路徑為0-4-1-2-0;然後,將客戶8作為第2臺配送車輛服務的第1個客戶,若能滿足問題的約束條件,則可將客戶7作為第2臺配送車輛服務的第2個客戶,若仍能滿足問題的約束條件,則可將客戶6作為第2臺配送車輛服務的第3個客戶,若仍能滿足問題的約束條件,則可將客戶9作為第2臺配送車輛服務的第4個客戶,若此時不能滿足問題的約束條件,則說明客戶9不能由第2臺配送車輛服務,由此可得第2臺車輛的配送路徑為0-8-7-6-0:仍按上述方法可將解中的其他客戶也依次加入到其他車輛的配送路徑中。採用這種表示方法,也可以得到配送路徑數小於車輛總檯數的配送路徑方案。若某個解中的排在最後的若干個客戶不能納入到車輛的配送路徑中,則說明該解為一個不可行解。與前述客戶與虛擬配送中心共同排列的表示方法相比,這種解的表示方法佔用的計算機儲存量較少,表示也較為直觀,也容易產生可行解。
3.2、解的評價:
用客戶直接排列表示方法產生的解所確定的配送路徑方案,能夠滿足每條配送路徑上各客戶需求量之和不超過配送車輛的最大載重量及每條配送路徑的長度不超過車輛一次配送的最大行駛距離的約束條件,但不能保證所有的客戶全部都能得到配送服務。對於某個解,若全部客戶均能納入到車輛的配送路徑中,則取該配送路徑方案的不可行路徑數M=0,表示該解為一個可行解;若排在最後的若干個客戶不能納入到車輛的配送路徑中,則取該配送路徑方案的不可行路徑條數M=1,表示該解為一個不可行解,該配送路徑方案的目標函式值為Z,並設對每條不可行路徑的懲罰權重為Pw,(該權重可根據目標函式的取值範圍取一個相對較大的正數),則該解的評價值E可用公式(3.1)計算(E值越小,表示解的質量越高)。這種解的評價方法,體現了用罰函式法處理約束條件的思想。

3.3、演算法策略的確定:
(1)編碼方法:採用客戶直接排列的編碼方法。
(2)適應度函式:採用公式(3.2)作為適應度評估函式。即首先對某個個體進行解碼操作,得到該個體對應的配送路徑方案的不可行路徑數M和目標函式值Z,將M和Z代入公式即可計算出該個體的適應度f。
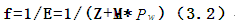
(3)選擇策略:採用最佳個體儲存與賭輪選擇相結合的選擇策略。其具體操作方法為:將每代群體中的N個個體按適應度由大到小排列,排在第一位的個體效能最優,按照最佳個體儲存選擇策略,將它複製一個直接進入下一代,並排在第一位。下一代群體的另N-1個個體需要根據前代群體的N個個體的適應度,採用賭輪選擇法產生。
(4)交叉運算元:採用類OX交叉方法。在實際運算中,交叉操作是以概率 ,發生的。
(5)變異運算元:採用多次對換變異技術。在實際運算中,變異操作是以概率 ,發生的,一旦變異操作發生,則用隨機方法產生交換次數J,對所需變異操作的個體的基因進行J次對換(對換基因的位置也是隨機產生的)。
(6)終止準則:採用進化指定代數的終止準則。
3.4、演算法的結構:
{輸入無時限單向配送車輛路徑問題的已知條件:
輸入執行引數,如群體規模N,終止進化代數T,交叉概率Pc,變異概率Pm,
執行變異操作時的基因換位次數J,對不可行路徑的懲罰權重Pw等;
隨機產生初始化群體P(0),當前進化代數t=0;
計算P(0)中每個個體的適應度;
while(t<指定進化終止代數T)do
{將本代中適應度最高的個體複製一個,直接插入到新群體P(t+1)中;
根據本代個體的適應度及賭輪選擇策略,計算群體內每個個體的選擇概率Pi;
for(k=0;k<N;k=k+2)
{根據選擇概率Pi從P(t)中選擇兩個父體;
r=random[0,1];
if(r≤交叉概率Pc)對選擇的兩個個體用類OX法執行交叉操作,並將
生成的兩後代插入到新群體P(t+1)中;
else
{r=random[0,1];
if(r≤變異概率Pm)對父代個體1執行變異操作,並將變異後的個
體插入到新群體P(t+1)中;
else將父代個體1複製一個,直接插入到新群體P(t+1)中;
r=random[0, 1];
if(r≤變異概率Pm)對父代個體2執行變異操作,並將變異後的個
體插入到新群體P(t+1)中;
else將父代個體2複製一個,直接插入到新群體P(t+1)中;
}
}
計算P(t+1)中每個個體的適應度;
t=t+1;
}
輸出計算結果,即最終解所對應的配送路徑方案和目標函式值;
}
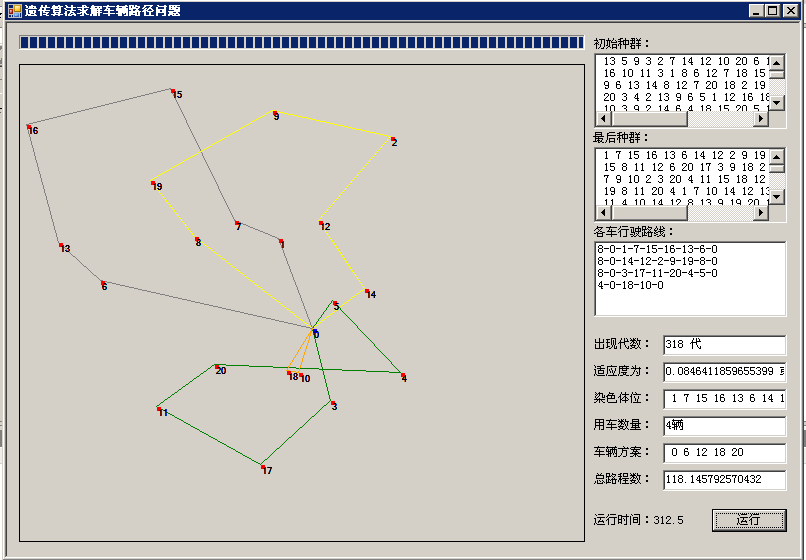
3.5、執行截圖: