浮點數是我們在程式裡常用的資料型別，它在記憶體中到底是怎麼樣的形式存在，是我瞭解之前是覺得好神奇，以此記錄，作為學習筆記。

現代計算機中，一般都以IEEE 754標準儲存浮點數，這個標準的在記憶體中儲存的形式為：

對於不同長度的浮點數，階碼與小數位分配的數量不一樣，如下：

對於32位的單精度浮點數，數符分配是1位，階碼分配了8位，尾數分配了是23位。

根據這個標準，我們來嘗試把一個十進位制的浮點數轉換為IEEE754標準表示。

例如：178.125

1. 先把浮點數分別把整數部分和小數部分轉換成2進位制
   1. 整數部分用除2取餘的方法，求得：10110010
   2. 小數部分用乘2取整的方法，求得：001
   3. 合起來即是：10110010.001
   4. 轉換成二進位制的浮點數，即把小數點移動到整數位只有1，即為：1.0110010001 * 2^111，111是二進位制，由於左移了7位，所以是111
2. 把浮點數轉換二進位制後，這裡基本已經可以得出對應3部分的值了
   1. 數符：由於浮點數是整數，故為0.(負數為1)
   2. 階碼 : 階碼是需要作移碼運算，在轉換出來的二進位制數裡，階數是111(十進位制為7)，對於單精度的浮點數，偏移值為01111111(127)[偏移量的計算是：2^(e-1)-1, e為階碼的位數，即為8，因此偏移值是127]，即：111+01111111 = 10000110
   3. 尾數：小數點後面的數，即0110010001
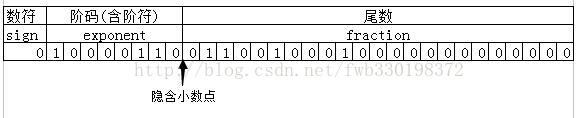
   4. 最終根據位置填到對位的位置上：
   5. 

可能有個疑問：小數點前面的1去哪裡了？由於尾數部分是規格化表示的，最高位總是“1”，所以這是直接隱藏掉，同時也節省了1個位出來儲存小數，提高精度