LDA線性判別分析Python程式
阿新 • • 發佈:2019-02-03
需要匯入的包
# -*- coding: utf-8 -*-
import numpy as np
import csv
from matplotlib import pyplot as plt
import math匯入資料集
def read_iris():
from sklearn.datasets import load_iris
from sklearn import preprocessing
data_set = load_iris()
data_x = data_set.data
label = data_set.target + 1 iris資料集
有三類,4個特徵
初始類標籤是從0開始的,加一後從1開始。
preprocessing.scale(data_x, axis=0, with_mean=True, with_std=True, copy=False)
是對資料進行標準化
# 特徵均值,計算每類的均值,返回一個向量
def class_mean(data,label,clusters) 輸入特徵資料集,類標籤,類別個數
計算每類資料的均值
用於計算散度矩陣
# 計算類內散度
def within_class_SW(data,label,clusters):
m = data.shape[1]
S_W = np.zeros((m,m))
mean_vectors = class_mean(data,label,clusters)
for 計算類內散度,散度矩陣式
首先計算類內均值
對每一類中的每條資料減去均值進行矩陣乘法(列向量乘以行向量,所得的矩陣秩為1,線代中講過 )
相加,就是類內散度矩陣
def between_class_SB(data,label,clusters):
m = data.shape[1]
all_mean =np.mean(data,axis = 0)
S_B = np.zeros((m,m))
mean_vectors = class_mean(data,label,clusters)
for cl ,mean_vec in enumerate(mean_vectors):
n = data[label==cl+1,:].shape[0]
mean_vec = mean_vec.reshape(4,1) # make column vector
all_mean = all_mean.reshape(4,1)# make column vector
S_B += n * (mean_vec - all_mean).dot((mean_vec - all_mean).T)
#print S_B
return S_B計算類間散度矩陣,這裡某一類的特徵用改類的均值向量體現。
C個秩為1的矩陣的和,資料集中心是整體資料的中心,S_B是秩為C-1
def lda():
data,label=read_iris();
clusters = 3
S_W = within_class_SW(data,label,clusters)
S_B = between_class_SB(data,label,clusters)
eig_vals, eig_vecs = np.linalg.eig(np.linalg.inv(S_W).dot(S_B))
#print S_W
#print S_B
for i in range(len(eig_vals)):
eigvec_sc = eig_vecs[:,i].reshape(4,1)
print('\nEigenvector {}: \n{}'.format(i+1, eigvec_sc.real))
print('Eigenvalue {:}: {:.2e}'.format(i+1, eig_vals[i].real))
eig_pairs = [(np.abs(eig_vals[i]), eig_vecs[:,i]) for i in range(len(eig_vals))]
eig_pairs = sorted(eig_pairs, key=lambda k: k[0], reverse=True)
W = np.hstack((eig_pairs[0][1].reshape(4,1), eig_pairs[1][1].reshape(4,1)))
print 'Matrix W:\n', W.real
print data.dot(W)
return W 類內散度矩陣
類間散度矩陣
計算
所資料集中有d個特徵
特徵值為0的有:
我們只需要考慮前
寫了這個程式發現,若投影矩陣式
n是資料的數量
d是特徵數
k是降維後的維數
上篇中說的投影后的資料是:
這個兩個不一樣啊???
這樣就說得通了,只是資料的表現形式不一樣。
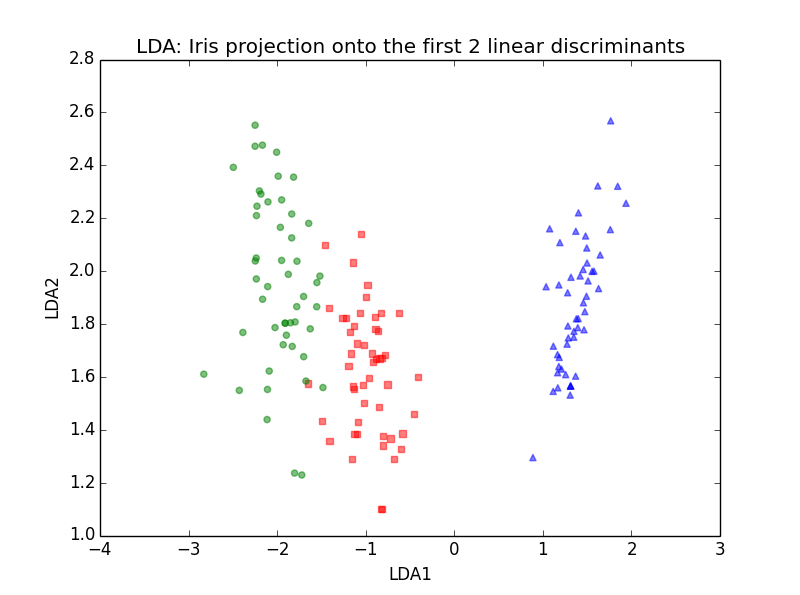
下面是用上面程式投影后的資料的散點圖
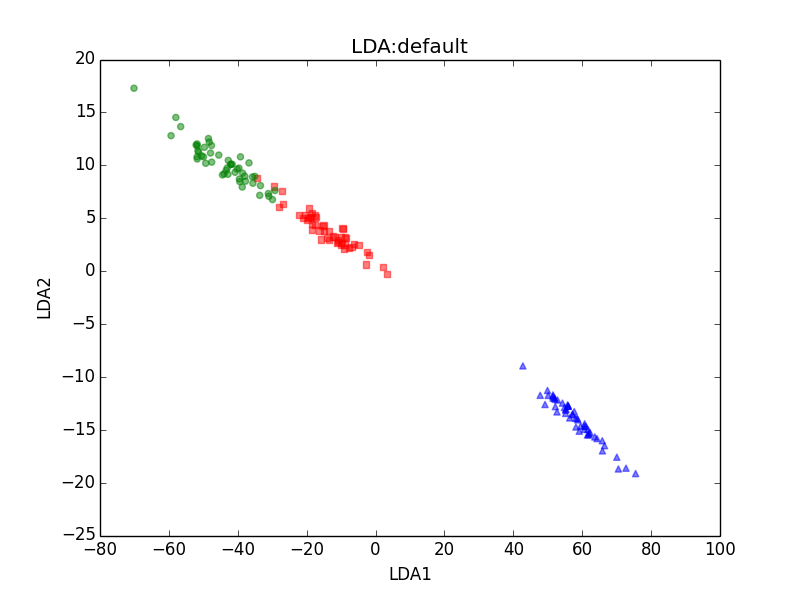
下面的是用
def plot_lda():
data,labels = read_iris()
W = lda()
Y = data.dot(W)
#print Y
ax= plt.subplot(111)
for label,marker,color in zip(range(1,4),('^','s','o'),('blue','red','green')):
plt.scatter(x=Y[:,0][labels == label],
y=Y[:,1][labels == label],
marker = marker,
color = color,
alpha = 0.5,
)
plt.xlabel('LDA1')
plt.ylabel('LDA2')
plt.title('LDA: Iris projection onto the first 2 linear discriminants')
plt.show()
def default_plot_lda():
Y = sklearnLDA()
data,labels = read_iris()
ax= plt.subplot(111)
for label,marker,color in zip(range(1,4),('^','s','o'),('blue','red','green')):
plt.scatter(x=Y[:,0][labels == label],
y=Y[:,1][labels == label],
marker = marker,
color = color,
alpha = 0.5,
)
plt.xlabel('LDA1')
plt.ylabel('LDA2')
plt.title('LDA:default')
plt.show()
def sklearnLDA():
from sklearn import datasets
from sklearn.lda import LDA
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
lda = LDA(n_components=2)
X_r2 = lda.fit(X, y).transform(X)
return X_r2
if __name__ =="__main__":
#lda()
#sklearnLDA()
plot_lda()
default_plot_lda()