原文地址

LDA演算法入門

一． LDA演算法概述：

線性判別式分析(Linear Discriminant Analysis, LDA)，也叫做Fisher線性判別(Fisher Linear Discriminant ,FLD)，是模式識別的經典演算法，它是在1996年由Belhumeur引入模式識別和人工智慧領域的。性鑑別分析的基本思想是將高維的模式樣本投影到最佳鑑別向量空間，以達到抽取分類資訊和壓縮特徵空間維數的效果，投影后保證模式樣本在新的子空間有最大的類間距離和最小的類內距離，即模式在該空間中有最佳的可分離性。因此，它是一種有效的特徵抽取方法。使用這種方法能夠使投影后模式樣本的類間散佈矩陣最大，並且同時類內散佈矩陣最小。就是說，它能夠保證投影后模式樣本在新的空間中有最小的類內距離和最大的類間距離，即模式在該空間中有最佳的可分離性。

二． LDA假設以及符號說明：

假設對於一個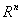空間有m個樣本分別為x1,x2,……xm 即 每個x是一個n行的矩陣，其中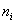表示屬於i類的樣本個數，假設有一個有c個類，則。

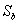………………………………………………………………………… 類間離散度矩陣

………………………………………………………………………… 類內離散度矩陣

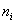………………………………………………………………………… 屬於i類的樣本個數

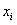 …………………………………………………………………………… 第i個樣本

 …………………………………………………………………………… 所有樣本的均值

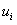 …………………………………………………………………………… 類i的樣本均值

三． 公式推導，演算法形式化描述

根據符號說明可得類i的樣本均值為：

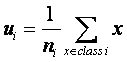 …………………………………………………………………… （1）

同理我們也可以得到總體樣本均值：

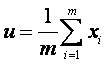………………………………………………………………………… （2）

根據類間離散度矩陣和類內離散度矩陣定義，可以得到如下式子：

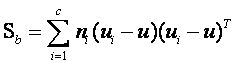  ……………………………………………… （3）

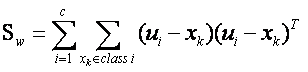…………………………………… （4）

當然還有另一種類間類內的離散度矩陣表達方式：

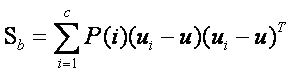
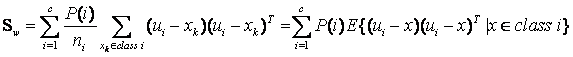其中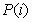是指i類樣本的先驗概率，即樣本中屬於i類的概率（），把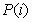代入第二組式子中，我們可以發現第一組式子只是比第二組式子都少乘了1/m，我們將在稍後進行討論，其實對於乘不乘該1/m，對於演算法本身並沒有影響，現在我們分析一下演算法的思想，

我們可以知道矩陣的實際意義是一個協方差矩陣，這個矩陣所刻畫的是該類與樣本總體之間的關係，其中該矩陣對角線上的函式所代表的是該類相對樣本總體的方差（即分散度），而非對角線上的元素所代表是該類樣本總體均值的協方差（即該類和總體樣本的相關聯度或稱冗餘度），所以根據公式（3）可知（3）式即把所有樣本中各個樣本根據自己所屬的類計算出樣本與總體的協方差矩陣的總和，這從巨集觀上描述了所有類和總體之間的離散冗餘程度。同理可以的得出（4）式中為分類內各個樣本和所屬類之間的協方差矩陣之和，它所刻畫的是從總體來看類內各個樣本與類之間（這裡所刻畫的類特性是由是類內各個樣本的平均值矩陣構成）離散度，其實從中可以看出不管是類內的樣本期望矩陣還是總體樣本期望矩陣，它們都只是充當一個媒介作用，不管是類內還是類間離散度矩陣都是從巨集觀上刻畫出類與類之間的樣本的離散度和類內樣本和樣本之間的離散度。

LDA做為一個分類的演算法，我們當然希望它所分的類之間耦合度低，類內的聚合度高，即類內離散度矩陣的中的數值要小，而類間離散度矩陣中的數值要大，這樣的分類的效果才好。

這裡我們引入Fisher鑑別準則表示式：

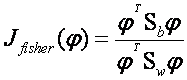…………………………………………………………… （5）

其中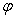為任一n維列向量。Fisher線性鑑別分析就是選取使得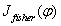達到最大值的向量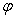作為投影方向，其物理意義就是投影后的樣本具有最大的類間離散度和最小的類內離散度。

我們把公式（4）和公式（3）代入公式（5）得到：

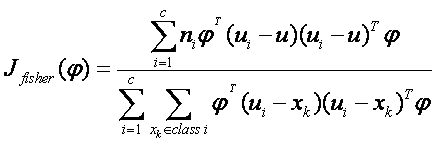
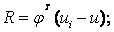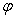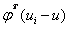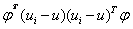我們可以設矩陣其中可以看成是一個空間，也就是說是構成的低維空間（超平面）的投影。也可表示為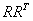，而當樣本為列向量時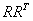，即表示在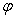空間的幾何距離的平方。所以可以推出fisher線性鑑別分析表示式的分子即為樣本在投影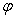空間下的類間幾何距離的平方和，同理也可推出分母為樣本在投影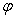空間下的類內幾何距離的平方差，所以分類問題就轉化到找一個低維空間使得樣本投影到該空間下時，投影下來的類間距離平方和與類內距離平方和之比最大，即最佳分類效果。

所以根據上述思想，即通過最優化下面的準則函式找到有一組最優鑑別向量構成的投影矩陣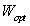（這裡我們也可以看出1/m可以通過分子分母約掉，所以前面所提到的第一組公式和第二組公式所表達的效果是一樣的）.

……………… （6）

可以證明，當為非奇異（一般在實現LDA演算法時，都會對樣本做一次PCA演算法的降維，消除樣本的冗餘度，從而保證是非奇異陣，當然即使為奇異陣也是可以解的，可以把或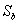對角化，這裡不做討論，假設都是非奇異的情況）時，最佳投影矩陣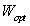的列向量恰為下來廣義特徵方程

………………………………………………………………………… （7）

的d個最大的特徵值所對應的特徵向量(矩陣的特徵向量)，且最優投影軸的個數d<=c-1.

根據（7）式可以推出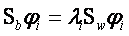……………………………………………… （8）

又由於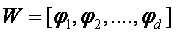

下面給出驗證：把（7）式代入（6）式可得：

四． 演算法的物理意義和思考

4.1 用一個例子闡述LDA演算法在空間上的意義

下面我們利用LDA進行一個分類的問題：假設一個產品有兩個引數來衡量它是否合格，

我們假設兩個引數分別為：

所以我們可以根據上圖表格把樣本分為兩類，一類是合格的，一類是不合格的，所以我們可以建立兩個資料集類：

cls1_data =

    2.9500    6.6300

    2.5300    7.7900

    3.5700    5.6500

3.1600    5.4700

cls2_data =

    2.5800    4.4600

    2.1600    6.2200

    3.2700    3.5200

其中cls1_data為合格樣本，cls2_data為不合格的樣本，我們根據公式（1），（2）可以算出合格的樣本的期望值，不合格類樣本的合格的值，以及總樣本期望：

E_cls1 =

3.0525    6.3850

E_cls2 =

2.6700    4.7333

E_all =

2.8886    5.6771

我們可以做出現在各個樣本點的位置：

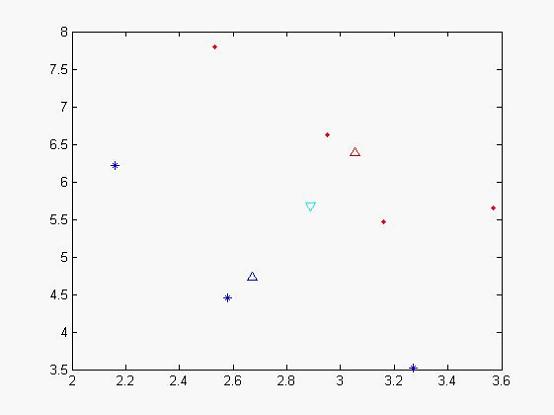
圖一

其中藍色‘*’的點代表不合格的樣本，而紅色實點代表合格的樣本，天藍色的倒三角是代表總期望，藍色三角形代表不合格樣本的期望，紅色三角形代表合格樣本的期望。從x，y軸的座標方向上可以看出，合格和不合格樣本區分度不佳。

我們在可以根據表示式（3），（4）可以計算出類間離散度矩陣和類內離散度矩陣：

Sb =

    0.0358    0.1547

0.1547    0.6681

Sw =

    0.5909   -1.3338

   -1.3338    3.5596

我們可以根據公式（7），（8）算出特徵值以及對應的特徵向量：

L =

    0.0000         0

         0    2.8837

對角線上為特徵值，第一個特徵值太小被計算機約為0了

與他對應的特徵向量為

V =

   -0.9742   -0.9230

0.2256   -0.3848

根據取最大特徵值對應的特徵向量：（-0.9230,-0.3848)，該向量即為我們要求的子空間，我們可以把原來樣本投影到該向量後 所得到新的空間（2維投影到1維，應該為一個數字）

new_cls1_data =

   -5.2741

   -5.3328

   -5.4693

   -5.0216

為合格樣本投影后的樣本值

new_cls2_data =

   -4.0976

   -4.3872

   -4.3727

為不合格樣本投影后的樣本值，我們發現投影后，分類效果比較明顯，類和類之間聚合度很高，我們再次作圖以便更直觀看分類效果

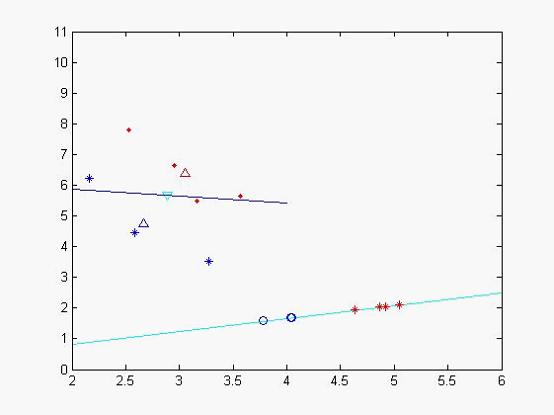
圖二

藍色的線為特徵值較小所對應的特徵向量，天藍色的為特徵值較大的特徵向量，其中藍色的圈點為不合格樣本在該特徵向量投影下來的位置，二紅色的‘*’符號的合格樣本投影后的資料集，從中個可以看出分類效果比較好（當然由於x，y軸單位的問題投影不那麼直觀）。

我們再利用所得到的特徵向量，來對其他樣本進行判斷看看它所屬的型別，我們取樣本點

（2.81，5.46），

我們把它投影到特徵向量後得到：result = -4.6947 所以它應該屬於不合格樣本。

4.2 LDA演算法與PCA演算法

在傳統特徵臉方法的基礎上，研究者注意到特徵值打的特徵向量（即特徵臉）並一定是分類效能最好的方向，而且對K-L變換而言，外在因素帶來的影象的差異和人臉本身帶來的差異是無法區分的，特徵連在很大程度上反映了光照等的差異。研究表明，特徵臉，特徵臉方法隨著光線，角度和人臉尺寸等因素的引入，識別率急劇下降，因此特徵臉方法用於人臉識別還存在理論的缺陷。線性判別式分析提取的特徵向量集，強調的是不同人臉的差異而不是人臉表情、照明條件等條件的變化，從而有助於提高識別效果。

（說明：以上是本人蔘閱文獻以及自己獨立思考理解所作，由於水平有限難免有紕漏以及錯誤之處，希望讀者諒解，歡迎通過郵件跟我交流）

 PDF 版本可以這裡下http://download.csdn.net/source/2228368 （推薦浙江大學蔡登教授編寫的關於LDA的程式碼：http://www.cad.zju.edu.cn/home/dengcai/Data/code/LDA.m）

--------------------- 本文來自 warmyellow 的CSDN 部落格 ，全文地址請點選：https://blog.csdn.net/warmyellow/article/details/5454943?utm_source=copy