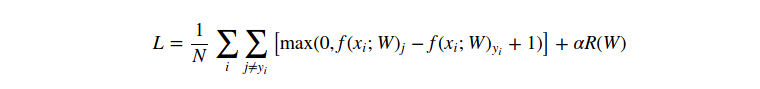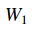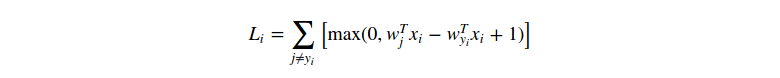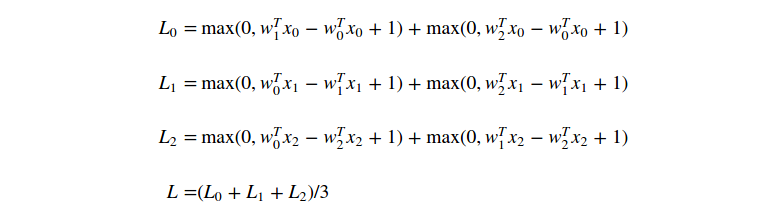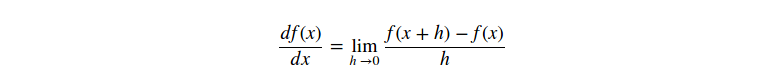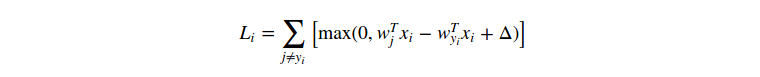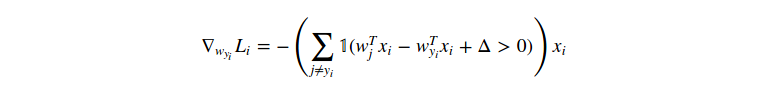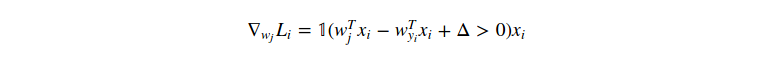########################################################################3

內容列表：

１．介紹

２．視覺化損失函式

３．最優化

3.1．策略１：隨機搜尋

3.2．策略２：隨機區域性搜尋

3.3．策略３：跟隨梯度

４．計算梯度

４.1．有限差分（Numerically with finite differences）

 4 .2 . 微積分計算（Analytically with calculus）

５．梯度下降

６．總結

############################################################################

Introduction

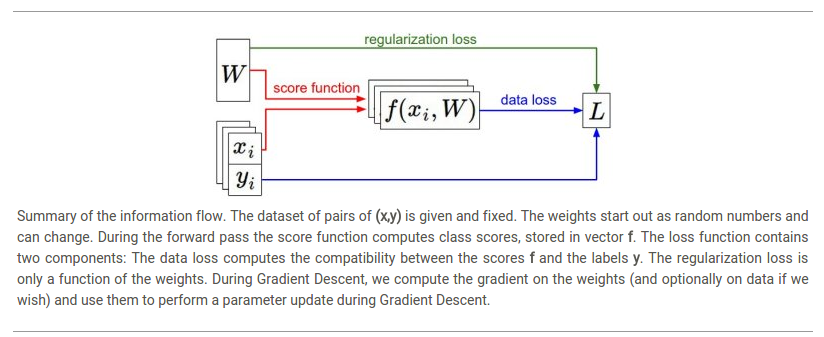
前一節，我們介紹了影象分類任務中兩個關鍵的部分：

１．一個（引數化的）成績函式（score function）：用於把原始畫素值對映為類別成績（e.g.　線性函式）

２．一個損失函式（loss function）：用於衡量一組給定的引數在計算得到的成績和真正類別結果的一致性上的滿意程度。我們看到了很多方法（e.g. Softmax/SVM）

具體的，回憶線性函式的格式為，同時SVM損失函式格式如下：

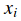
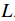
如果引數W設定合理，那麼對於樣本的預測結果會與真正結果相一致，並且也會有一個極低的損失值。現在我們將要去介紹第三個也是最後一個關鍵部分：最優化（optimization

）。最優化就是發現能夠最小化損失函式值的這組引數W的過程。

Foreshadowing（預告）：一旦我們理解了這三個核心元件是如何互動的，我們將重溫第一個元件（引數化對映函式）然後擴充套件至比線性函式更加複雜的形式：首先是神經網路，然後是卷積神經網路。而損失函式和最優化處理則相對保持不變。

Visualizing the loss function

本節我們看到的損失函式通常都被定義在高維空間中（e.g.　在CIFAR-10中，一個線性分類器的權重矩陣的大小為），這很難去視覺化。然而，我們可以通過一些方法去獲得視覺化畫面，比如沿著射線（1維）截斷高維空間，或者沿著平面（2維）截斷高維空間。舉個例子，我們可以生成一個隨機權重向量（相對於這個空間中的一個點來說），然後沿著一條射線記錄一路上的損失函式值。也就是說，我們可以生成一個隨機的方向矩陣

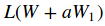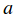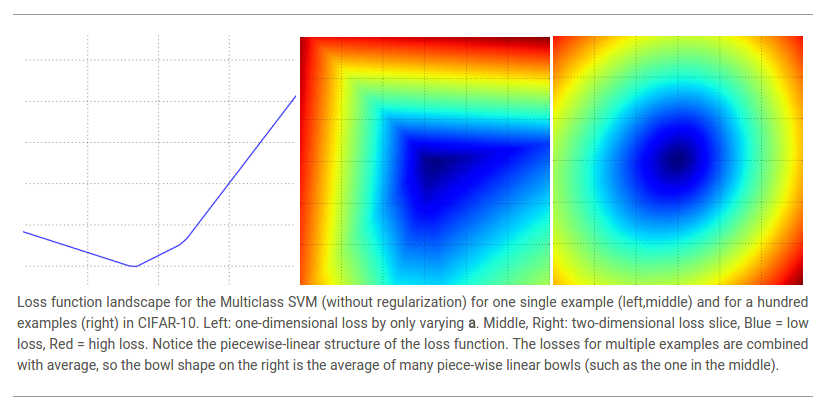
，然後沿著這個方向計算損失函式值，計算公式為，以的值為x軸，以損失函式值為y軸，生成一個點圖。我們同樣可以用同樣的方式來計算兩個維度上的損失函式值，計算公式為，其中為變化引數。在一個圖中，分別對應於x軸，y軸，然後損失函式值可以通過顏色來視覺化：

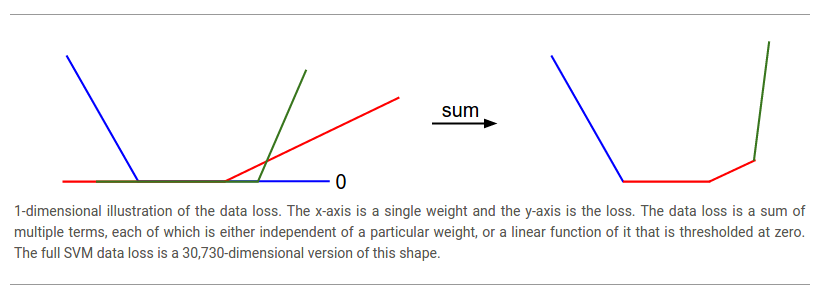
我們可以通過考察數學式子來解釋分段線性結構的損失函式。公式如下：

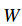
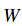
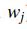
從公式中可以明顯看出，每一個樣本的資料損失（data loss）就是引數的線性函式（zero-threshold due to themax(0,-) function）的求和。另外，引數的每一行有時會是正的（如果這一行相對應於錯誤的類別），有時會是負的（如果這一行相對應於正確的類別）。讓這一過程更加明晰，考慮一個簡單的資料集，擁有三個1維點和3個類別。完整的SVM損失（沒有規則化）如下：

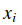
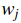
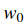
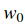
因為這些樣本都是一維的，所以資料和權重都是數字。比如，Looking at ，some terms above are linear function of   and each is clamped at zero. 視覺化結果如下：

說句題外話，你可能已經從它的碗的形狀中看出SVM損失函式是凸函式（convex function）的一個特例。有很多的文獻致力於如何最有效的最小化這些函式的型別，你也可以參加Stanford的關於這個主題的課程（convex optimization）。一旦我們把成績函式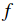擴充套件為神經網路，那麼我們的損失函式將不再是凸函式，它的視覺化影象也不在是碗狀而是複雜，崎嶇不平的形狀。

Non-differentiable loss functions. 作為一個技術說明，損失函式中的kinks（由於the max operation）使得損失函式不可微，因為在這些kinks上沒有梯度。然而，thesubgradient仍然存在並且經常被使用。本節中，我們假定術語subgradient和gradient可以相互替換。

Optimization

重申一遍，損失函式量化了一組特定權重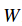的質量。最優化的目標是去發現能夠最小化損失函式值的那一組權重。我們現在將motivate以及慢慢開發一個方法來優化損失函式。對於之前有過學習的人來說，這一節可能看起來很奇怪，因為我們將使用的工作樣本（the SVM loss）是一個凸問題，但是請注意，我們的目標是最終優化神經網路，而神經網路使不能輕易地使用任何凸優化理論開發的工具來優化的。

Strategy #1：A first very bad idea solution：Random search

第一個想到的方法是嘗試使用各種不同的權重，然後比較出最好的那一組。流程如下：

# assume X_train is the data where each column is an example (e.g. 3073 x 50,000)
# assume Y_train are the labels (e.g. 1D array of 50,000)
# assume the function L evaluates the loss function

bestloss = float("inf") # Python assigns the highest possible float value
for num in xrange(1000):
  W = np.random.randn(10, 3073) * 0.0001 # generate random parameters
  loss = L(X_train, Y_train, W) # get the loss over the entire training set
  if loss < bestloss: # keep track of the best solution
    bestloss = loss
    bestW = W
  print 'in attempt %d the loss was %f, best %f' % (num, loss, bestloss)

# prints:
# in attempt 0 the loss was 9.401632, best 9.401632
# in attempt 1 the loss was 8.959668, best 8.959668
# in attempt 2 the loss was 9.044034, best 8.959668
# in attempt 3 the loss was 9.278948, best 8.959668
# in attempt 4 the loss was 8.857370, best 8.857370
# in attempt 5 the loss was 8.943151, best 8.857370
# in attempt 6 the loss was 8.605604, best 8.605604
# ... (trunctated: continues for 1000 lines)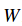

在上面的程式碼中，我們嘗試了1000中不同的權重向量，其中有一些比其他的權重效果更好。我們從這些權重中找出結果最好的那一組，然後在測試集中使用這組權重進行測試：

# Assume X_test is [3073 x 10000], Y_test [10000 x 1]
scores = Wbest.dot(Xte_cols) # 10 x 10000, the class scores for all test examples
# find the index with max score in each column (the predicted class)
Yte_predict = np.argmax(scores, axis = 0)
# and calculate accuracy (fraction of predictions that are correct)
np.mean(Yte_predict == Yte)
# returns 0.1555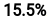

從程式碼中得知，最好的權重得到的檢測精度大約為。Given that guessing classes completely at random achieves only 10%, that’s not a very bad outcome for a such a brain-dead random search solution!

Core idea：iterative refinement（迭代求精）. 事實證明我們可以得到更好的結果。上面操作的核心思想如下：發現最好的那一組權重是一件很困難或者說是不可能完成的任務（尤其當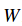包含整個複雜的神經網路的權重的時候），但是如果是去發現一組可以比目前權重所得結果更加好的權重則明顯沒那麼困難。換句話說，我們的方法是以一組隨機權重開始，然後不斷迭代求精，使得每一次能比前一此好一點即可。

Blindfolded hiker analogy. 有一個很好的類比，想象你是一個在一個丘陵地形上的旅行者，但你是蒙著眼睛的，這是你想要達到底部。在CIFAR-10中，因為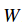的維度是30730x10，所以這座山高30730個維度。在山上的每一個維度，你都可以收穫一個特定的損失（the height of the terrain）。

Strategy #2：Random Local Search

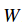
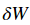
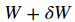
你能想到的第一個策略是在任意方向上都嘗試邁出一步，只有這個方向能夠往下才繼續下一步。第二個策略具體如下：我們將以一個隨機開始，生成一個隨機的改變值，如果權重計算得到的損失值更小，那麼我們將進行一次權重更新。程式碼如下：

W = np.random.randn(10, 3073) * 0.001 # generate random starting W
bestloss = float("inf")
for i in xrange(1000):
  step_size = 0.0001
  Wtry = W + np.random.randn(10, 3073) * step_size
  loss = L(Xtr_cols, Ytr, Wtry)
  if loss < bestloss:
    W = Wtry
    bestloss = loss
  print 'iter %d loss is %f' % (i, bestloss)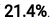

上述步驟同樣進行了1000次，而此次在測試影象集上得到的精度為。This is better, but still wasteful and computationally expensive.

Strategy #3：Following the Gradient

在前一節我們試圖在權重空間中找到一個能夠優化權重向量的方向（同時得到一個更小的損失）。事實證明，並不需要去隨機搜尋這個好的方向：我們可以計算得出這個最好的方向，在數學上可以證明這是一個最速下降的方向（其步長大小接近與0）。這個方向也和損失損失函式的梯度相關。 In our hiking analogy, this approach roughly corresponds to feeling the slope of the hill below our feet and stepping down the direction that feels steepest.

相對於一維函式，這個斜率就是任何一個點的函式瞬時速率的改變。梯度是斜率的泛化表示，不再僅使用單個數字而是用一組向量表示。另外，梯度也就是一組輸入空間中每一個維度斜率（通常被稱為導數（derivative））的向量。一維函式的導數表示式如下：

當函式的輸入為一組向量而不是單個數字時，我們稱這些導數為偏導數（partial derivatives），導數就是每一個維度的偏導數的集合。

Computing the gradient

有兩種計算梯度的方式：一種緩慢的，近似的但很簡單的方式（數值梯度，numerical gradient）；另一種快速，精確但容易出錯的方式（解析梯度，analytic gradient），它要求微積分。

Computing the gradient numerically with finite differences

上面給出的公式允許我們計算數值梯度。有一個通用的公式，使用一個函式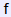，在某一個向量上計算梯度。公式如下：

def eval_numerical_gradient(f, x):
  """ 
  a naive implementation of numerical gradient of f at x 
  - f should be a function that takes a single argument
  - x is the point (numpy array) to evaluate the gradient at
  """ 

  fx = f(x) # evaluate function value at original point
  grad = np.zeros(x.shape)
  h = 0.00001

  # iterate over all indexes in x
  it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
  while not it.finished:

    # evaluate function at x+h
    ix = it.multi_index
    old_value = x[ix]
    x[ix] = old_value + h # increment by h
    fxh = f(x) # evalute f(x + h)
    x[ix] = old_value # restore to previous value (very important!)

    # compute the partial derivative
    grad[ix] = (fxh - fx) / h # the slope
    it.iternext() # step to next dimension

  return grad

上面的梯度公式計算了輸入向量x的梯度：通過迭代每一維，然後計算損失函式沿著該維的偏導數。到最後，變數擁有整個梯度值。

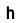
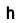
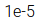
Practical considerations. 在數學公式中，梯度指的是在變數增長趨向於0的情況下，函式的改變數，但在實際生活中，只需設定為一個很小的值即可（比如即可）。而在理想情況下，你想要去使用一個最小的步長（不會導致數值問題）。另外，實際生活中使用中心差分公式（the centered difference formula）來計算數值梯度效果更好：。具體細節請看wiki。

我們可使用上面的公式來計算任何公式的任何一個具體點的梯度。下面在CIFAR-10上計算某幾個隨機點的損失函式的梯度：

# to use the generic code above we want a function that takes a single argument
# (the weights in our case) so we close over X_train and Y_train
def CIFAR10_loss_fun(W):
  return L(X_train, Y_train, W)

W = np.random.rand(10, 3073) * 0.001 # random weight vector
df = eval_numerical_gradient(CIFAR10_loss_fun, W) # get the gradient

梯度告訴我們損失函式在每個維度上的斜率，所以我們可以使用梯度進行權重更新：

loss_original = CIFAR10_loss_fun(W) # the original loss
print 'original loss: %f' % (loss_original, )

# lets see the effect of multiple step sizes
for step_size_log in [-10, -9, -8, -7, -6, -5,-4,-3,-2,-1]:
  step_size = 10 ** step_size_log
  W_new = W - step_size * df # new position in the weight space
  loss_new = CIFAR10_loss_fun(W_new)
  print 'for step size %f new loss: %f' % (step_size, loss_new)

# prints:
# original loss: 2.200718
# for step size 1.000000e-10 new loss: 2.200652
# for step size 1.000000e-09 new loss: 2.200057
# for step size 1.000000e-08 new loss: 2.194116
# for step size 1.000000e-07 new loss: 2.135493
# for step size 1.000000e-06 new loss: 1.647802
# for step size 1.000000e-05 new loss: 2.844355
# for step size 1.000000e-04 new loss: 25.558142
# for step size 1.000000e-03 new loss: 254.086573
# for step size 1.000000e-02 new loss: 2539.370888
# for step size 1.000000e-01 new loss: 25392.214036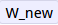

Update in negative gradient direction. 在上面的程式碼中，我們利用梯度值更新權重，更新的方向與梯度方向相反，因為我們希望損失函式變小而不是變大。

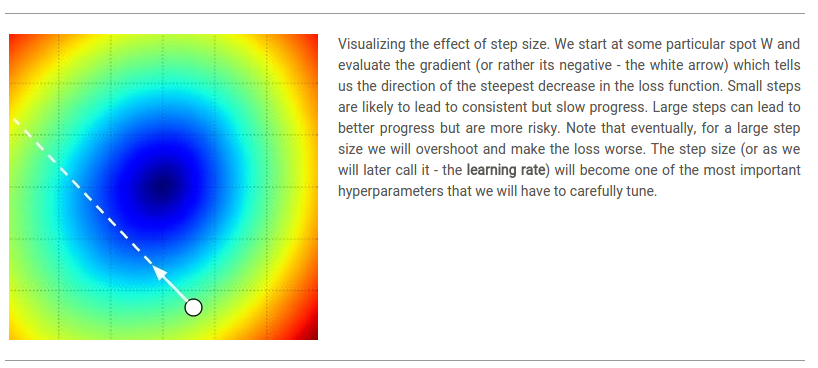
Effect of step size. 梯度告訴我們函式可以增長最快的方向，但並沒有告訴我們沿著這個方向應該走多遠。在本門課程之後會講到，步長的選擇是訓練一個神經網路最重要的超引數設定問題之一。在之前矇眼下山的類比中，我們能感覺到山坡有一個傾斜的方向，但我們應該跨出的步長並不確定。如果我們小心翼翼地挪動腳步，為了有一個正確但很小的進步（這相對應於有一個小的步長）。相反，我們可以大步向下降最快的方向前進，但這樣的效果可能不一定好。從上面的程式碼例子中可以看出，在某一些點上如果步長太大，會產生一個更高的損失就好像我們“overstep”。

A problem of efficiency. 你可能已經注意到，計算數值梯度的複雜性和引數個數之間呈線性關係。在我們的例子中，我們共有30730個引數，因此我們必須執行30731次損失函式計算後才能計算得出梯度值，也才能進行一次引數更新。這個問題會變得更加糟糕，因為現在的神經網路的引數輕易就可以達到上百萬個。確切的說，這種方法是不可延續的，所以我們必須找到其他更好的辦法。

Computing the gradient analytically with Calculus

數值梯度通過有限差分逼近方式易於計算，但缺點是它是近似的（因為我們會選擇一個小的h值，而在梯度公式中，h的值被定義為趨近於0），並且計算量非常大。計算梯度的第二種方式是微積分，它允許我們直接推匯出梯度（不是近似的），並且可以快速的進行計算。然而，它在應用過程中更容易出錯，所以實際使用時，常用做法是計算解析梯度，然後和數值梯度進行比較來判斷是否正確。這個步驟稱為梯度檢查（gradient check）。

單個數據點的SVM損失函式公式如下：

我們可以微分這個函式。舉個例子，計算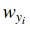的梯度，公式如下：

其中是一個指示函式，如果條件表示式為true，則輸出條件表示式的值；否則，輸出為0。上面表示式看起來很難記，但只要你程式碼實現它，你就會發現很容易去統計不符合預期的類別的數目（and hence contributed to the loss function），並且資料向量被縮放的值就是梯度。注意，這個梯度值僅僅相對應於權重的某一行（相對應於正確類別的）。For the other rows where  the gradient is:

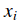
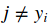
如果你理解了上面的梯度公式，那麼就可以直接應用這個表示式去執行梯度更新。

Gradient Descent

現在我們能夠計算損失函式的梯度。反覆計算梯度，然後進行梯度更新的過程稱為梯度下降（Gradient Descent）。Its vanilla version 如下：

# Vanilla Gradient Descent

while True:
  weights_grad = evaluate_gradient(loss_fun, data, weights)
  weights += - step_size * weights_grad # perform parameter update

這個簡單的迴圈是所有神經網路庫的核心。還有其他的方式可以執行最優化操作（e.g. LBFGS），但是梯度下降是目前優化神經網路的損失函式的最常用的方式。本節課中，我們會在這個迴圈中新增一些額外的功能（put some bells and whistles on the details of this loop）（e.g. 更新等式的確切細節），但是核心思想並沒有改變。

Mini-batch gradient descent. 在大規模的應用中（比如ILSVRC挑戰），訓練資料可能以百萬計。因此，為了執行一次引數更新而計算整個訓練集的損失函式顯得有點浪費。解決這一問題的常用方法是批量處理訓練資料的梯度。舉個例子，in current state of the art ConvNets，整個訓練集共120萬個樣本，典型的批量處理的數量為256。下面為批量處理引數更新的程式碼：

# Vanilla Minibatch Gradient Descent

while True:
  data_batch = sample_training_data(data, 256) # sample 256 examples
  weights_grad = evaluate_gradient(loss_fun, data_batch, weights)
  weights += - step_size * weights_grad # perform parameter update

這種方式能夠得到好的結果的原因是因為訓練資料都是相關的。要了解這一點，考慮一個極端的情況，就是ILSVRC上的120萬個影象事實上是由1000張不同的圖片複製而得到的（一張圖片對應一個類，或者每張圖片有1200張相同的複製）。很明顯，我們計算的1200個相同副本的梯度都是一樣的，and when we average the data loss over all 1.2 million images we would get the exact same loss as if we only evaluated on a small subset of 1000。實際上，資料集並不會擁有重複的圖片，小批量的梯度是對所有損失函式的梯度的一個很好的近似。因此，通過計算小批量梯度來執行更頻繁的引數更新，可以更快的收斂。

批量更新的最極端的例子是批量處理的數目僅為一個樣本。這個過程稱為隨機梯度下降（Stochastic Gradient Descent，SGD）（有時也稱為線上梯度下降（on-line gradient descent））。不過在實際使用中並不多見，因為向量程式碼優化，一次計算100個樣本的梯度比計算100次單個樣本的梯度更有效率。儘管技術上來說，SGD表示一次僅計算一個樣本的梯度，但是實際上人們使用SGD表示小批量梯度更新（i.e. MGD指“小批量梯度更新”，BGD表示“批量梯度更新”，這些不太使用）。小批量的大小是一個超引數，但是通常不需要交叉驗證來得到。它通常是基於記憶體約束（if any），或者設定一些值，比如32，64或者128。We use powers of 2 in practice because many vectorized operation implementations work faster when their inputs are sized in powers of 2.

Summary

本節中

１）我們開發一個高維優化山坡（high-dimensional optimization landscpe）去視覺化損失函式，我們的目標是儘量去到達底部。我們開發的類比是一個蒙著眼睛的徒步旅行者想要達到山底。特別的，我們看到SVM損失函式是分段線性的，而且是碗狀的。

２）我們說明了通過迭代求解（iterative refinement）的方式來優化損失函式的想法，即我們以一組隨機權重開始，逐步求解，直到損失值是最小的。

３）我們知道了函式的梯度（gradient）是最快上升的方向，我們討論了用有限差分逼近的方式來數值計算梯度，這種方式簡單卻效率不高（the finite difference being the value of h used in computing the numerical gradient）。

４）引數更新過程中，步長（step size，或者稱為學習速率，the learning rate）是一個略帶技巧性的設定：如果太低，那麼進展很慢；如果太高，進展可以更快，但是風險更大。我們在後面還會更加詳細的討論這個事情。

５）我們討論了數值梯度（numerical）計算和解析梯度（analytic）計算之間的權衡。數值梯度很簡單，但是它是近似計算，而且計算量很大。解析梯度計算準確，速度快，但是需要梯度推導，反而更容易出錯。實際上，我們經常使用解析梯度，然後進行梯度檢查（gradient check），就是和數值梯度比較效果。

６）介紹了梯度下降演算法：在一個迴圈中不斷迭代計算梯度，然後進行梯度更新。

Coming up：本節的核心思想就是計算損失函式的梯度，自變數為權重。下一節我們將使用鏈式法則提高解析梯度計算的效率，或者稱為反向傳播（backpropagation）。This will allow us to efficiently optimize relatively arbitrary loss functions that express all kinds of Neural Networks, including Convolutional Neural Networks.