人生，就像一個很大的棧演變。出生時赤條條地來到這個世界，慢慢地長大，漸漸地變老，最終還得赤條條地離開世間。

思路分析：

上面是一個迷宮地圖，在地圖上，0 代表牆，1 代表通路。

迷宮是回溯法和棧的綜合應用。

下面給出完整的思路和尋路演算法：

這裡我們只研究一種情況：地圖只有一條路徑可以出去。

尋路演算法按照上下左右的順序進行遍歷和判斷。

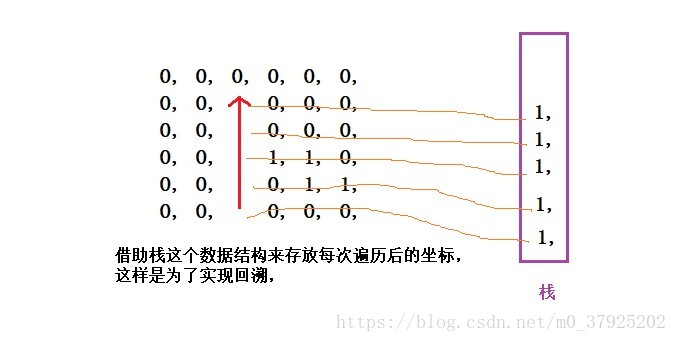
從入口出發，按照上下左右的順序尋路，每次的路徑座標Pos放到棧中，存放座標是為了方便回溯。如上圖，直到向上沒有通路了，再檢視當前位置，左，右是否有通路，實際如圖所示，沒有。那麼就取棧頂座標，回退一步，再檢視左右是否有通路。如此迴圈。

如果不停地回退，導致棧中沒有元素，這就說明回退到了迷宮入口。那麼就可以說明此迷宮沒有通路。

在迷宮中還有一點值得注意就是對是否為地圖邊界 的判斷。

下面給出核心程式碼：

迷宮定義：

#define N 10
typedef struct Pos{
    int _row;
    int _col;
}Pos;

typedef struct Maze
{
    int _mz[N][N];
    Pos _entry;
}Maze;

尋路演算法：

int CheckIsAccess(Maze *m, Pos pos)
{
    if(pos._row >= 0 && pos
 
._row < N
       && pos._col >= 0 && pos._col < N
       && m->_mz[pos._row][pos._col] == 1)
       {
           return 1;
       }
       return 0;
}


void MazeGetPath(Maze* m)
{
    Stack s;
    StackInit(&s, 10);
    StackPush(&s, m->_entry);

    while
 
(StackEmpty(&s) != 0)
    {
        //1,入口   2，下一個可以走的位置  3，回溯的上一個位置
        cur = StackTop(&s);
        m->_mz[cur._row][cur._col] = 2;

        if(cur._col == N-1)
        {
            printf("找到通路了\n");
            return;
        }

        Pos next = cur;

        //上
        next._row -= 1;
        if(CheckIsAccess(m, next) == -1)
        {
            StackPush(&s, next);
            continue;
        }

        //下
        next = cur;
        next._row += 1;
        if(CheckIsAccess(m, next) == 1)
        {
            StackPush(&s, next);
            continue;
        }

        //左
        next = cur;
        next._col -= 1;
        if(CheckIsAccess(m, next) == 1)
        {
            StackPush(&s, next);
            continue;
        }

        //右
        next = cur;
        next._col += 1;
        if(CheckIsAccess(m, next) == 1)
        {
            StackPush(&s, next);
            continue;
        }

        //回溯
        StackPop(&s);
    }
    printf("沒有通路\n");
}