概率分佈-二項分佈、多項分佈
1. 兩點分佈
就是一次伯努利實驗,拋硬幣
2. 二項分佈
多次獨立的伯努利實驗,
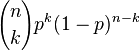
3. 多項分佈
定義:設可能的實驗結果可分成k組: A1、A2、…、An ,每次實驗結果落入某一組Ai的機率為sigma Pi=
1, where i =1 to k。如果共進行了n次獨立的實驗,實驗結果落入某個組的次數為x1、x2、…、xk , 的概率為
相關推薦
概率分佈-二項分佈、多項分佈
1. 兩點分佈 就是一次伯努利實驗,拋硬幣 2. 二項分佈 多次獨立的伯努利實驗, 3. 多項分佈 定義:設可能的實驗結果可分成k組: A1、A2、…、An ,每次實驗結果落入某一組Ai的機率為sigma Pi= 1, where i =1 to k。如果共進行了n次獨
伯努利分佈、二項分佈、Beta分佈、多項分佈和Dirichlet分佈與他們之間的關係,以及在LDA中的應用
在看LDA的時候,遇到的數學公式分佈有些多,因此在這裡總結一下思路。 一、伯努利試驗、伯努利過程與伯努利分佈 先說一下什麼是伯努利試驗: 維基百科伯努利試驗中: 伯努利試驗(Bernoulli trial)是隻有兩種可能結果的單次隨機試驗。 即:對於一個隨機變數而言,P(X
伯努利分佈、二項分佈、多項分佈、貝塔分佈、狄利克雷分佈、高斯分佈
伯努利分佈: 伯努利分佈(Bernoulli distribution)又名兩點分佈或0-1分佈,介紹伯努利分佈前首先需要引入伯努利試驗(Bernoulli trial)。 伯努利試驗是隻有兩種可能結果的單次隨機試驗,即對於一個隨機變數X而言: 伯努利試驗都可以表達為“是或否”
離散分佈——二項分佈、多項分佈、超幾何分佈
二項分佈 伯努利實驗 介紹二項分佈前,先了解一下伯努利實驗。 比如一個雞蛋是否能成功孵出小雞,扔硬幣,進入商店的人是否購買了東西,一個正在生產的產婦是生男生女,這些都是伯努利實驗。它滿足以下條件:1、每次只可能有兩種結果;2、兩次實驗之間互不影響。
關於Beta分佈、二項分佈與Dirichlet分佈、多項分佈的關係
在機器學習領域中,概率模型是一個常用的利器。用它來對問題進行建模,有幾點好處:1)當給定引數分佈的假設空間後,可以通過很嚴格的數學推導,得到模型的似然分佈,這樣模型可以有很好的概率解釋;2)可以利用現有的EM演算法或者Variational method來學習。通
echarts生成餅狀圖、柱狀圖、多項柱狀圖的引數介紹
1.餅圖 html程式碼: <div id="SexDistri" style="width: 100%;height: 50%;"></div> 下面的柱狀圖的html程式碼也與此類似。 js程式碼: var SexDistributi
logistic regression(二項 logistic 與 多項logistic )
邏輯斯蒂迴歸 基本思想 數學推導 基於R的案例 結論 基本思想 這一講給大家介紹一下,廣義線性迴歸模型當中的一個最為典型的模型,邏輯斯底迴歸(logistic regression)。估計大家都見過。我們最長用到的是二值邏輯斯底迴歸,多項邏輯斯底書
“十三五”國家重點出版規劃項目、教育部項目暨上海精品課程“網絡安全”技術更新推出
安全 分享 png tex vpd mage shadow alt 技術分享 “十三五”國家重點出版規劃項目、教育部項目暨上海精品課程“網絡安全”技術更新推出,歡迎光臨指導、資源共享!“十三五”國家重點出版規劃項目、教育部項目暨上海精品課程“網絡安全”技術更新推出
002-創建基本項目-新項目、空項目、已有項目
rmi copies .html ack 結構 eat bundles 依賴項 fig 一、創建基本項目 您可以使用create-react-app軟件包或創建一個空的IntelliJ IDEA項目並在其中安裝React。create-react-app項目地址:ht
Java基礎總結(二)----集合、多執行緒、io、虛擬機器等
Java集合 java集合框架的結構 List介面 List介面通常表示一個列表(陣列、佇列、連結串列、棧等),其中的元素可以重複,常用實現類為ArrayList和LinkedList,另外還有不常用的Vector。另外,LinkedList還
伯努利分佈、二項分佈、幾何分佈、超幾何分佈、泊松分佈
導語 對於任何一個學習概率論的童鞋來說,各種分佈都是很頭痛的一件事情,本篇主要討論的是離散型隨機變數. 伯努利分佈 伯努利分佈就
伯努利分佈、二項分佈、泊松分佈、指數分佈簡介
伯努利分佈: 首先說伯努利分佈, 這個是最簡單的分佈,就是0-1分佈 以拋硬幣為例, 為正面的概率為p, 反面的概率為q 是一種離散型概率分佈,也是很多分佈的基礎 二項分佈: 還是以伯努利分佈為基礎,假設伯努利分佈中得1的概率為p, 0的概率為q 那麼二項
數學(3) 各種數學分佈,高斯,伯努利,二項,多項,泊松,指數,Beta,Dirichlet
打算這裡記錄各種數學分佈,隨時更新 正態分佈 正態分佈又名高斯分佈。 若隨機變數X服從一個數學期望為μ,標準差為σ的正態分佈,則記為X~N(μ,σ2)。 其中期望μ決定了分佈位置,標準差σ決定了分佈幅度。 概率密度函式為: f(x)=1σ2π
概率分佈(多項分佈,Dirichlet分佈)
在機器學習領域中,概率模型是一個常用的利器。用它來對問題進行建模,有幾點好處:1)當給定引數分佈的假設空間後,可以通過很嚴格的數學推導,得到模型的似然分佈,這樣模型有很好的概率解釋;2)可以利用現有的EM演算法或者Variational method來學習。通常
泊松分佈 二項分佈 正態分佈之間的聯絡,與繪製高斯分佈圖
基礎知識 二項分佈有兩個引數,一個 n 表示試驗次數,一個 p 表示一次試驗成功概率。現在考慮一列二項分佈,其中試驗次數 n 無限增加,而 p 是 n 的函式。 1.如果 np 存在有限極限 λ,則這列二項分佈就趨於引數為 λ 的 泊松分佈。反之,如果 np 趨於
從零開始學Xamarin.Forms(二) 環境搭建、創建項目
官方 log targe 4.4 pad jdk 新建文件夾 ini pos 一、環境搭建 Windows下環境搭建: 1.下載並安裝jdk 、Android SDK和NDK。當然還須要 VS2013 update 2(VS2010、VS2012均可)以上
2015級C++第7周項目 友元、共享數據保護、多文件結構
執行 pub 程序 block tails 一個 date類 能夠 tracking 【項目1-成員函數、友元函數和一般函數有差別】參考解答 (1)閱讀以下的程序,體會凝視中的說明(要執行程序,請找到課程主頁並復制代碼) //例:使用成員函數、友
Android Gradle Plugin指南(三)——依賴關系、android庫和多項目配置
tool 全部 ocs 共享 項目路徑 多項目配置 path 用戶 so文件 原文地址:http://tools.android.com/tech-docs/new-build-system/user-guide#TOC-Dependencies-Android-L
008-shiro與spring web項目整合【二】認證、授權、session管理
添加 ner != efi ebs ref private date err 一、認證 1、添加憑證匹配器 添加憑證匹配器實現md5加密校驗。 修改applicationContext-shiro.xml: <!-- realm -->
用 Spring Boot 實現電商系統 Web API (二)創建多模塊項目
ble jin play 正常 ota autowired ips 功能 bind 大型項目,需要將代碼按不同功能,分成不同模塊,這樣比較好管理和閱讀代碼,也有助於多人協作。 一、項目結構 1.1 模塊說明 項目分成5個模塊,分別如下: 模塊名稱 說明 webapi
