HDU 1272 小希的迷宮 並查集 (判斷任意2個點是否有且僅有一條路徑可以相通)
阿新 • • 發佈:2019-02-05
Problem Description
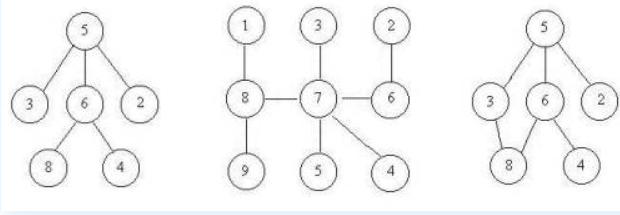
上次Gardon的迷宮城堡小希玩了很久(見Problem B),現在她也想設計一個迷宮讓Gardon來走。但是她設計迷宮的思路不一樣,首先她認為所有的通道都應該是雙向連通的,就是說如果有一個通道連通了房間A和B,那麼既可以通過它從房間A走到房間B,也可以通過它從房間B走到房間A,為了提高難度,小希希望任意兩個房間有且僅有一條路徑可以相通(除非走了回頭路)。小希現在把她的設計圖給你,讓你幫忙判斷她的設計圖是否符合她的設計思路。比如下面的例子,前兩個是符合條件的,但是最後一個卻有兩種方法從5到達8。
Input
輸入包含多組資料,每組資料是一個以0 0結尾的整數對列表,表示了一條通道連線的兩個房間的編號。房間的編號至少為1,且不超過100000。每兩組資料之間有一個空行。
整個檔案以兩個-1結尾。
Output
對於輸入的每一組資料,輸出僅包括一行。如果該迷宮符合小希的思路,那麼輸出"Yes",否則輸出"No"。
Sample Input
6 8 5 3 5 2 6 4
5 6 0 0
8 1 7 3 6 2 8 9 7 5
7 4 7 8 7 6 0 0
3 8 6 8 6 4
5 3 5 6 5 2 0 0
-1 -1
Sample Output
Yes
Yes
No
題意:判斷通過這些點相連可以達到 任意兩個房間有且僅有一條路徑可以相通。
思路:因為任意兩個房間有且僅有一條路徑可以相通,所以只可以有一個根節點,注意尋找根節點的時候的方向問題
#include <iostream> #include <cstdio> #include <cstring> #include <string> #include <algorithm> #include <map> #include <set> #include <cmath> using namespace std; typedef long long ll; const int N = 100005; int flag[N]; int parent[N]; int root(int x) { return parent[x] == x ? x: parent[x]=root(parent[x]); } void make(int x,int y) { int fx=root(x); int fy=root(y); if(fx>fy) parent[fx]=fy; else parent[fy]=fx; } int main() { int a,b; while(scanf("%d%d",&a,&b)==2){ if(a==-1&&b==-1) break; for(int i=0;i<=100000;i++) parent[i]=i; memset(flag,0,sizeof(flag)); int F=0; while(1) { if(a==0&&b==0) break; if(root(a)==root(b)) //如果2個點再次相連則錯誤 F=1; make(a,b); flag[a]=1; //這2個點都到達過 flag[b]=1; scanf("%d%d",&a,&b); } if(F==1) printf("No\n"); else{ int sum=0; for(int i=0;i<=100000;i++) if(flag[i]&&parent[i]==i) //記錄根節點的個數 sum++; if(sum>1) printf("No\n"); else printf("Yes\n"); } } return 0; }