蝴蝶定理的英文是Butterfly Theorem，蝴蝶定理是古典歐氏平面幾何的最精彩的結果之一。

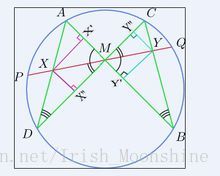
蝴蝶定理（Butterfly Theorem）：設M為圓內弦PQ的中點，過M作弦AB和CD。設AD和BC各相交PQ於點X和Y，則M是XY的中點。
去掉中點的條件，結論變為一個一般關於有向線段的比例式，稱為“坎迪定理”， 不為中點時滿足:1/MY-1/MX=1/MQ-1/MP ,這對2，3均成立。

證明：
霍納證法！
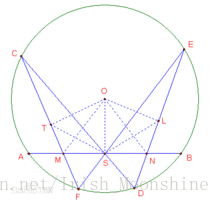
過O作OL⊥ED，OT⊥CF，垂足為L、T，
連線ON，OM，OS，SL，ST，易明△ESD∽△CSF
證法1:霍納證法
證法1:霍納證法
∴ES/CS=ED/FC
根據垂徑定理得：LD=ED/2，FT=FC/2
∴ES/CS=EL/CT
又∵∠E=∠C
∴△ESL∽△CST
∴∠SLN=∠STM
∵S是AB的中點所以OS⊥AB
∴∠OSN=∠OLN=90°
∴O，S，N，L四點共圓，（一中同長）
同理，O，T，M，S四點共圓
∴∠STM=∠SOM，∠SLN=∠SON
∴∠SON=∠SOM
∵OS⊥AB
∴MS=NS