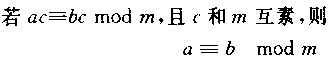同餘：

• 定義：設m≠0，若m∣a－b，即a－b＝km，則稱a與b同餘，餘數為m。
• 充要條件：a、b關於模m同餘的充要條件是整數a和b被同一正整數m除時，有相同的餘數。(a % m)=(b % m)意味a≡b (%m)
• 性質：
  
  

• 同餘類：根據整數模n所得的餘數，可以把整數分成n個等價類：[0],[1],…,[n-1]。
  包含整數的模n等價類為：[a]n={a+kn| k∈Z}。

• 例題：求3406寫成十進位數時的個位數.
  根據題意是要求a滿足3406 ≡a（mod 10）
  顯然32 ≡9 ≡－1 （mod 10），
  34 ≡1 （mod 10），
  從而3404 ≡1 （mod 10），
  因此3406 ≡ 3404 × 32 ≡9（mod 10）
  所以個位數是9.

模運算的運算規則

• （1）(a + b) % p = (a % p + b % p) % p
• （2）(a - b) % p = (a % p - b % p) % p
• （3）(a * b) % p = (a % p * b % p) % p
• （4）a ^ b % p = ((a % p)^b) % p
• 結合律：
  （5）((a+b) % p + c) % p = (a + (b+c) % p) % p
  （6）((a*b) % p * c)% p = (a * (b*c) % p) % p
• 交換律：
  （7）(a + b) % p = (b+a) % p
  （8）(a * b) % p = (b * a) % p
• 分配律：
  （9）(a+b) % p = ( a % p + b % p ) % p
  （10) ((a +b)% p * c) % p = ((a * c) % p + (b * c) % p) % p
• 重要定理：
  （11）若a≡b (% p)，則對於任意的c，都有(a + c) ≡ (b + c) (%p)
  （12）若a≡b (% p)，則對於任意的c，都有(a * c) ≡ (b * c)
  （13） 若a≡b (% p)，c≡d (% p)，則 (a + c) ≡ (b + d) (%p)，(a - c) ≡ (b - d) (%p)，
  (a * c) ≡ (b * d) (%p)，(a / c) ≡ (b / d) (%p)

乘法逆元：

• 定義：
  滿足a*k≡1 (mod p)的k值就是a關於p的乘法逆元。eg: 1=5*3-14 所以5關於模14的乘法逆元為3.

• 應用：
  當我們要求 (a/b) mod P 的值時，如果 a 很大，無法直接求得a/b的值時，我們就可以使用乘法逆元。我們可以通過求b關於P的乘法逆元k，將a乘上k再模P，即(a%P*k)。其結果與(a/b) mod P等價。