There is a complete graph containing n vertices, the weight of the i-th vertex is wi.
The length of edge between vertex i and j (i≠j) is .
Calculate the length of the shortest path from 1 to n

.

Input

The first line of the input contains an integer T

(1≤T≤10)

denoting the number of test cases.
Each test case starts with an integer n (1≤n≤105) denoting the number of vertices in the graph.
The second line contains n integers, the i-th integer denotes wi (1≤wi≤105)

.

Output

For each test case, print an integer denoting the length of the shortest path from 1

to n

.

Sample Input

1
3
1 3 5

Sample Output

2

從前一個點可以任意選擇下一個點， 每個點有一個權值， 點和點之間的距離是，權值差的絕對值開根號再向下取整，求從1 到n最短距離。

剛開始做這個題， 覺得是個水題， （實際上確實是個水題），寫了個 n ^ 2的記憶化搜尋， 抱著僥倖心理交了一次， 不出意外的超時了~

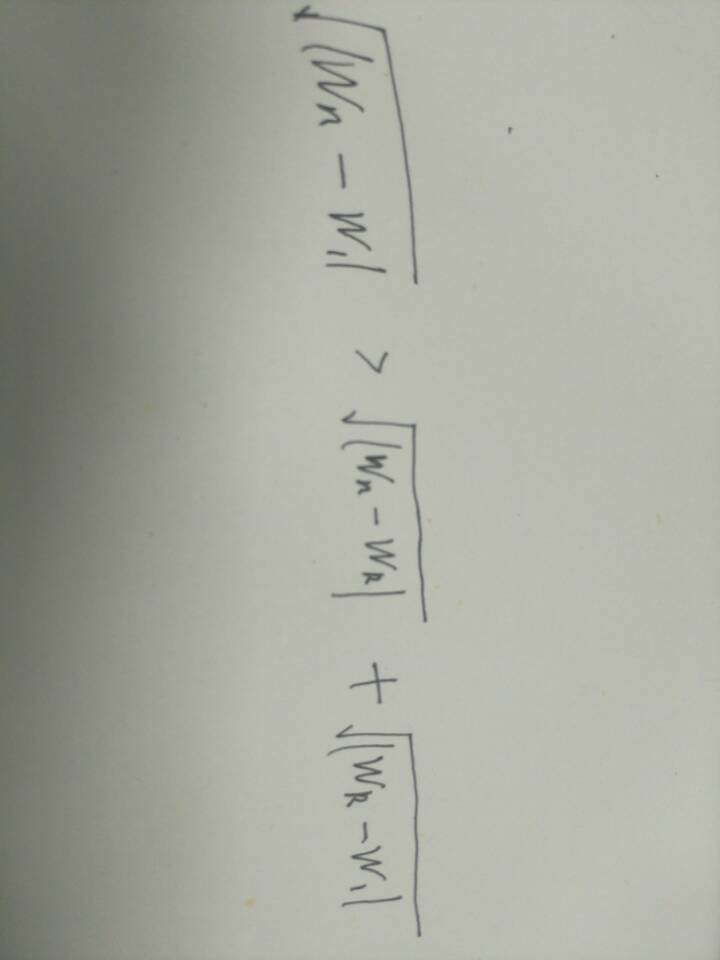
實際上我們可以假設有某中間點k， 使得直接從1到n的路線鬆弛， 那麼有

兩邊平方就會發現， k的存在是矛盾的，所以知道最短距離是從1直接到n。

AC程式碼：

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
    int i, j, T, ans, n, q, m;
    int s[100005];
    scanf("%d", &T);
    while(T--){
        scanf("%d", &n);
        for(i = 1;i <= n;i++)
            scanf("%d", &a);
        m = abs(s[1] - s[n]);
        ans = (int)sqrt(m * 1.0);
        printf("%d\n", ans);
    }
    return 0;
}