前向神經網路和 BP 演算法詳解

一、神經網路的概念詳解

1.1、人工神經網路的基礎單元 — > 感知機

1.1.1、感知機模型講解

• 首先我們需要明確一點就是，針對於擁有核函式的 SVM 或者多隱層 + 啟用函式的多層神經網路，或者其他可以處理非線性可分的模型來說，感知機我們常稱為神經元，但也可以看成是兩層的神經網路( 即只有輸入層和輸出層，沒有隱層 )，雖然它只能處理線性可分問題，但它依然是我們學習神經網路和深度學習的基石。
  
  
  
  
  
• 圖中對應的符號含義如下：
  
  • 輸入（x1 ，…，xn）
  • 偏移b 和 突觸權重（w1 ，…，wn），注意，我們下面推到是使用
    θi${\theta }_i$ 代替 wi 進行公式推導。
  • 組合函式c（·）
  • 啟用函式a（·）
  • 輸出y
    
    
• 用數學的語言來說，如果我們有m個樣本，每個樣本對應於n維特徵和一個二元類別輸出，如下：
  (x(0)1,x(0)2,...x(0)n,y0),(x(1)1,x(1)2,...x(1)n,y1),...(x(m)1,x(m)2,...x(m)n,ym)$$(x_1^{(0)},x_2^{(0)},...x_n^{(0)},y_0),(x_1^{(1)},x_2^{(1)},...x_n^{(1)},y_1),...(x_1^{(m)},x_2^{(m)},...x_n^{(m)},y_m)$$
• 我們的目的便是找一個超平面，即： θ0+θ1x1+...+θnxn=0${\theta }_0+{\theta }_1{x}_1+...+{\theta }_n{x}_n=0$ 讓把每個類別的樣本特徵帶入該方程時，要麼大於 0 ，要麼小於 0,從而使得樣本分居在超平面兩側，從而到達線性可分。一般如果樣本線性可分，則這樣的超平面會有多個解，不唯一。
  
  
• 為了簡化模型，我們增加一個 x0 = 1，使得超平面方程簡寫為 ∑i=0nθixi=0$\sum _{i=0}^n{\theta }_i{x}_i=0$ 進一步可寫向量形式為 θ∙x=0$\theta \bullet x=0$ 其中 θ$\theta$ 和 X 均為 n * 1 的向量，∙$\bullet$為內積，下面我們都用它表示超平面。
• 故感知機的模型可以定義為 y=sign(θ∙x)$y=sign(\theta \bullet x)$ ,其中sign 為啟用函式，它是符號函式，也稱為階躍函式。
  sign(x)={−11x<0x≥0$$sign(x)=\{\begin{array}{ll}-1& x<0\\ 1& x\ge 0\end{array}$$
  
  
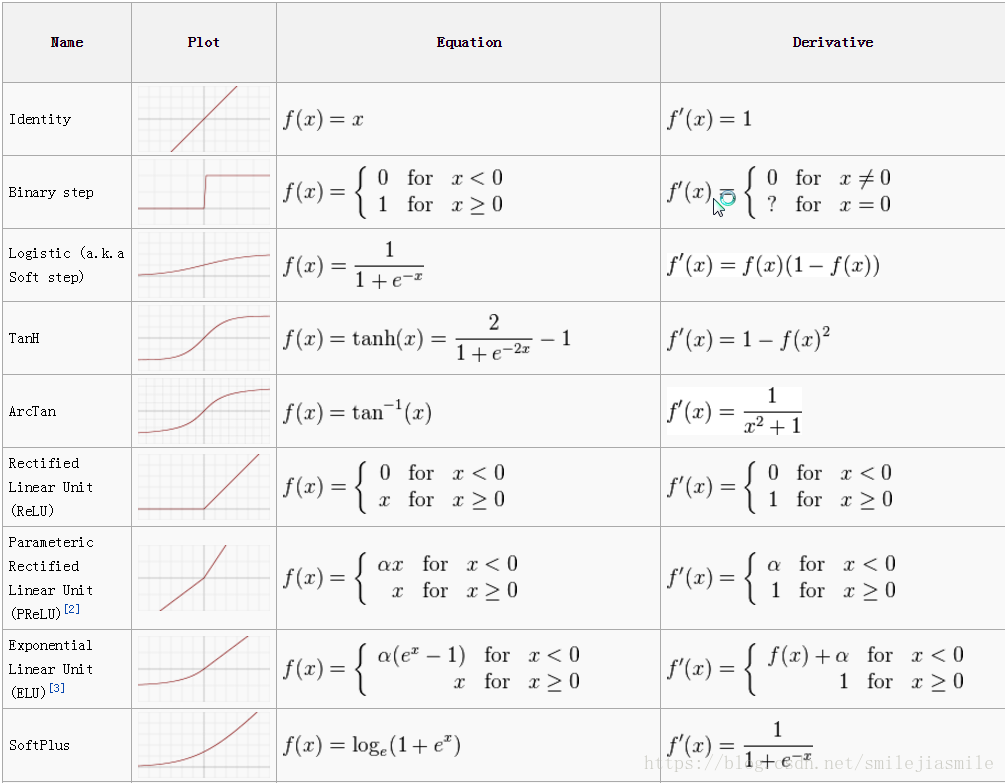
• 在多層神經網路中，我們可能用到其他的啟用函式,如下：

1.1.2 感知機模型損失函式

• 根據上面的分析，我們將 θ∙x>0$\theta \bullet$
  x>0的樣本類別輸出值取為1 ，而小於 0 的樣本類別取為 -1，這樣定義它的好處便是方便我們定義損失函式。因為有了上面的約定，正確分類的樣本滿足： yθ∙x>0$y\theta \bullet x>0$,而錯誤的分類樣本滿足 yθ∙x<0$y\theta \bullet x<0$。於是損失函式的優化方法便是期望使誤分類的所有樣本，到超平面的距離之和最小(即想讓誤分類樣本逐漸消失)。
  
  
• 由於yθ∙x<0$y\theta \bullet x<0$，所以對於每一個誤分類的樣本 i，到超平面的距離為： −y(i)θ∙x(i)/||θ||2$$-y^{(i)}\theta \bullet x^{(i)}/||\theta |{|}_2$$
• 其中，||θ||2$||\theta |{|}_2$ 為 L2範數。(若此處距離公式不理解，可自行查閱點到直線的距離，或者學習相關的機器學習相關章節)
• 接著，我們假設所有誤分類的點的集合為M，則所有誤分類的樣本到超平面的距離之和為：
  −∑xi∈My

  相關推薦

  前向神經網路和 BP 演算法詳解 --- 之 DNN

  前向神經網路和 BP 演算法詳解 一、神經網路的概念詳解 1.1、人工神經網路的基礎單元 — > 感知機 1.1.1、感知機模型講解 首先我們需要明確一點就是，針對於擁有核函式的 SVM 或者多隱層 + 啟用函式的多層神

  神經網路和BP演算法推導

  我的原文：www.hijerry.cn/p/53364.htm… 感知機 感知機（perceptron）於1957年由Rosenblatt提出，是一種二分類線性模型。感知機以樣本特徵向量作為輸入，輸出為預測類別，取正、負兩類。感知機最終學習到的是將輸入空間（特徵空間）劃分為正、負兩類的分離超平面，屬於判別

  神經網路和BP演算法

  5. 神經網路 5.1 前向傳播 神經網路分為很多層，包括輸入層、輸出層和中間的隱層。 使用的符號如下： a(j)i a i

  多層前饋神經網路及BP演算法

  1.多層前饋神經網路 首先說下多層前饋神經網路，BP演算法，BP神經網路之間的關係。多層前饋（multilayer feed-forward）神經網路由一個輸入層、一個或多個隱藏層和一個輸出層組成，後向傳播(BP)演算法在多層前饋神經網路上面進行學習，採用BP

  前饋神經網路，BP演算法

  單層感知機輸入層——>輸出層啟用函式在輸出層，常見啟用函式Logistic、softmax函式多層感知機（MLP）輸入層——>隱藏層——>輸出層啟用函式在隱藏層，線性變換預啟用+非線性啟用函式，資料分佈“線性可分”隱藏層所含神經元越多，可提取特徵越多常用啟用

  神經網路及反向傳播(bp)演算法詳解

        神經元和感知器的本質一樣神經元和感知器本質上是一樣的，只不過感知器的時候，它的啟用函式是階躍函式；而當我們說神經元時，啟用函式往往選擇為sigmoid函式或tanh函式。如下圖所示：    輸入節點     每一個輸入節點對應一個權值，輸入節點可以是任意數。

  前向神經網路小試身手

  三層全連線神經網路：輸入層（2個節點）、隱藏層（3個節點）、輸出層（1個節點） x為輸入，w1第一層節點的引數，w2第二層節點的引數，y為輸出 import tensorflow as tf w1 = tf.Variable(tf.random_normal((2, 3), stddev=1

  西瓜書5.5 程式設計實現BP神經網路——標準BP演算法、累積BP演算法

  這裡照著書上的公式，實現了一下標準BP演算法，和累積BP演算法，BP是error Back Propagation的意思，誤差逆傳播。BP網路通常是指用BP演算法訓練的多層前饋神經網路。程式碼是照著書本公式自己寫的，沒有參考網上的其他版本。 資料和程式碼地址：https:/

  機器學習——神經網路累積BP演算法

  在上篇的部落格介紹的“標準BP演算法”每次僅針對一個訓練樣例更新連線權和閾值，也就是說，BP演算法中的更新規則是基於單個的 推導而得，如果類似的推匯出基於累積誤差最小化的更新規則，就得到了累積誤差逆傳播

  feedforwardnet，前向神經網路

  前向神經網路，feedforward neural network。 語法是 feedforwardnet(hiddenSizes,trainFcn) hiddenSizes    Row vector of one or more hidden layer sizes

  神經網路與BP演算法推導

  導言 神經網路是深度學習基礎，BP演算法是神經網路訓練中最基礎的演算法。因此，對神經網路結構和BP演算法進行梳理是理解深度學習的有效方法。參考資料UFLDL，BP推導，神經網路教材。 神經網路結構 典型網路為淺層網路，一般2~4層。其結構如下圖所示：

  神經網路中BP演算法的原理與用Python實現原始碼

  （1）什麼是梯度下降和鏈式求導法則 1.梯度下降 假設我們有一個函式J(w),如下圖所示。 現在，我們要求當w等於什麼的時候，J(w)能夠取到最小值。從圖中我們知道最小值在初始位置的左邊，也就意味著如果想要使J(w)最小，w的值需要減小。而初始位置的切線斜率a>0

  卷積神經網路反向BP演算法公式推導

  博文轉載至：http://blog.csdn.net/celerychen2009/article/details/8964753 此篇博文只涉及到公式推導，如果想了解卷積神經網路的具體工作過程，可檢視轉載博文博主其它文件或者百度自己去看。轉載的文章涉及到的角下標大家注意下

  機器學習總結（七）：基本神經網路、BP演算法、常用啟用函式對比

  1.   神經網路 （1）為什麼要用神經網路？ 對於非線性分類問題，如果用多元線性迴歸進行分類，需要構造許多高次項，導致特徵特多學習引數過多，從而複雜度太高。 （2）常用的啟用函式及其優缺點 階

  從 0 開始機器學習 - 神經網路反向 BP 演算法！

  最近一個月專案好忙，終於擠出時間把這篇 BP 演算法基本思想寫完了，公式的推導放到下一篇講吧。 ## 一、神經網路的代價函式 神經網路可以看做是複雜邏輯迴歸的組合，因此與其類似，我們訓練神經網路也要定義代價函式，之後再使用梯度下降法來最小化代價函式，以此來訓練最優的權重矩陣。 ### 1.1 從邏輯迴歸

  深度學習 --- BP演算法詳解（誤差反向傳播演算法）

  本節開始深度學習的第一個演算法BP演算法，本打算第一個演算法為單層感知器，但是感覺太簡單了，不懂得找本書看看就會了，這裡簡要的介紹一下單層感知器： 圖中可以看到，單層感知器很簡單，其實本質上他就是線性分類器，和機器學習中的多元線性迴歸的表示式差不多，因此它具有多元線性迴歸的優點和缺點。

  DeepLearning tutorial（4）CNN卷積神經網路原理簡介+程式碼詳解

  分享一下我老師大神的人工智慧教程！零基礎，通俗易懂！http://blog.csdn.net/jiangjunshow 也歡迎大家轉載本篇文章。分享知識，造福人民，實現我們中華民族偉大復興！        

  深度學習 --- BP演算法詳解（BP演算法的優化）

  上一節我們詳細分析了BP網路的權值調整空間的特點，深入分析了權值空間存在的兩個問題即平坦區和區域性最優值，也詳細探討了出現的原因，本節將根據上一節分析的原因進行改進BP演算法，本節先對BP存在的缺點進行全面的總結，然後給出解決方法和思路，好，下面正式開始本節的內容： BP演算法可以完成非線性

  深度學習 --- BP演算法詳解（流程圖、BP主要功能、BP演算法的侷限性）

  上一節我們詳細推倒了BP演算法的來龍去脈，請把原理一定要搞懂，不懂的請好好理解BP演算法詳解，我們下面就直接把上一節推匯出的權值調整公式拿過來，然後給出程式流程圖，該流程圖是嚴格按照上一節的權值更新過程寫出的，因此稱為標準的BP演算法，標準的BP演算法中，每輸入一個樣本，都要回傳誤差並調整權值，

  作業系統：程序排程演算法詳解之FCFS和SPF篇

  前言：   在學習作業系統的時候，總是可以聽到一些與“排程”相關的東西。記得剛學計算機作業系統的時候，總是覺得除錯是一個很高大上的東西，不敢太深入地去接觸。這可能是因為學生時代的我在演算法方面並不強，