拉格朗日 SVM KKT
假設有分佈在Rd空間中的資料,我們希望能夠在該空間上找出一個超平面(Hyper-pan),將這一資料分成兩類。屬於這一類的資料均在超平面的同側,而屬於另一類的資料均在超平面的另一側。如下圖。
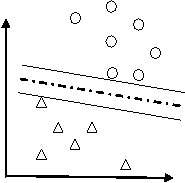
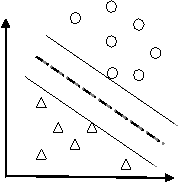
比較上圖,我們可以發現左圖所找出的超平面(虛線),其兩平行且與兩類資料相切的超平面(實線)之間的距離較近,而右圖則具有較大的間隔。而由於我們希望可以找出將兩類資料分得較開的超平面,因此右圖所找出的是比較好的超平面。可以將問題簡述如下:
設訓練的樣本輸入為xi
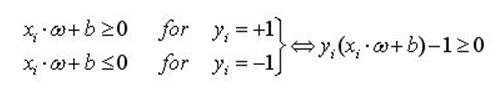 (1)
(1)
可以計算出,分類間隔為
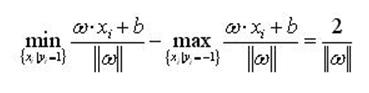 (2)
(2)
在約束式的條件下最大化分類間隔2/||ω||這可以通過最小化||ω||2的方法來實現。那麼,求解最優平面問題可以表示成如下的約束優化:即在條件式(1)的約束下,最小化函式
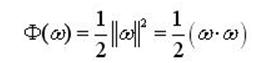 (3)
(3)
為了解決約束最優化問題,引入式(3)的拉格朗日函式
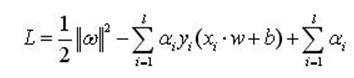 (4)
(4)
其中,αi>0為拉格朗日系數,現在的問題就是關於ω和b求L的最小值。
把式(4)分別對ω和b求偏微分並令其等於0,就可以把上述問題轉化為一個較簡單的"對偶"形式:
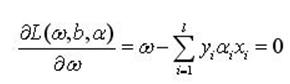 (5a)
(5a)
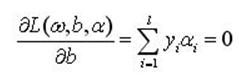 (5b)
(5b)
將得到的關係式:
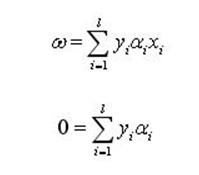 (6)
(6)
代入到原始拉格朗日函式,得到:
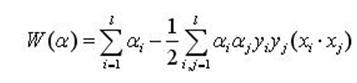 (7)
(7)
如果αi*為最優解,那麼
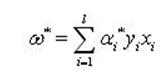 (8)
(8)
即最優超平面的權係數向量是訓練樣本向量的線性組合。
由於上述優化問題是一個Convex Problem,求解上述的SVM問題,須滿足KKT條件,這個優化問題的解必須滿足
 (9)
(9)
因此,對多數樣本ai將為0,取值不為零的ai對應於式(1)中等號成立的樣本即支援向量。
求解上述問題後得到的最優分類函式是
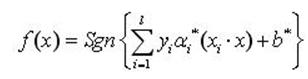 (10)
(10)
由於非支援向量對應的ai均為0,因此上式的求和實際上只對支援向量進行。最終的優化問題為
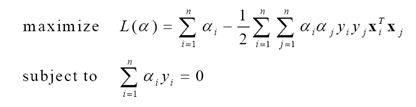 (11)
(11)
2. 非線性SVM
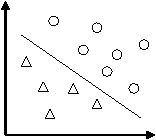

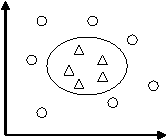
然而有的問題並不是線性可分的。但是可以通過一個適當的非線性函式φ,將資料由原始特徵空間對映到一個新的特徵空間,然後在新空間中尋求最優判定超平面。
所以問題(11)可以改寫為
 (12)
(12)
如果直接在高維空間計算φ(x),將會帶來維數災難。為了解決這一問題,引入核函式
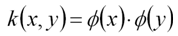 (13)
(13)
這樣問題(12)就變成
 (14)
(14)
常用的核函式有
-
多項式核
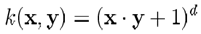
-
高斯徑向基核

-
Sigmoid核
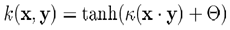
實際問題很少線性可分,雖然理論上可通過非線性對映得到線性可分的資料,但如何獲得這樣的對映,且避免過擬合,仍存在問題。所以更實際的策略是允許一定誤差。通常引入鬆弛變數ε,放鬆約束。這時問題描述改為下面的形式
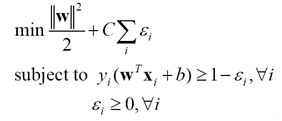 (15)
(15)
這樣的分類器稱為線性軟間隔支援向量分類機。轉化為拉格朗日乘子待定問題
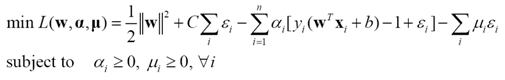 (16)
(16)
其KKT條件為
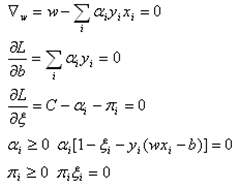 (17)
(17)
得到
 (18)
(18)
只要確定a,便可解出w,b.
將上述條件代入L中,得到新的優化問題:
 (19)
(19)
同樣地引入核函式,把這個軟間隔SVM的訓練表示為一個高維空間上的二次規劃問題
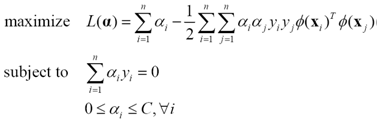 (20)
(20)
非線性SVM可用經典的二次規劃方法求解,但同時求解n個拉格朗日乘子涉及很多次迭代,計算開銷太大。所以一般採用Sequential Minimal Optimization(SMO)演算法。其基本思路是每次只更新兩個乘子,迭代獲得最終解。計算流程可表示如下
For i=1:iter
- 根據預先設定的規則,從所有樣本中選出兩個
- 保持其它拉格朗日乘子不變,更新所選樣本對應的拉格朗日乘子
End
SMO演算法的優點在於,只有兩個變數的二次規劃問題存在解析解。
關鍵的技術細節在於,一是在每次迭代中,怎樣更新乘子;二是怎樣選擇每次迭代需要更新的乘子。
假定在某次迭代中,需要更新樣本x1,x2對應的拉格朗日乘子a1,a2.
這個小規模的二次規劃問題可以寫成
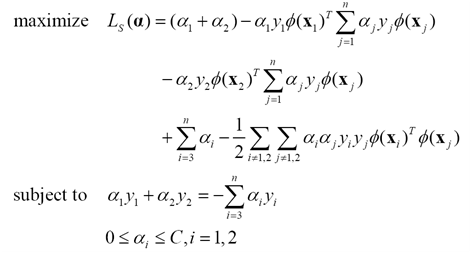 (21)
(21)
進一步簡化為
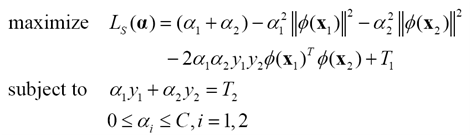 (22)
(22)
步驟1 計算上下界L和H
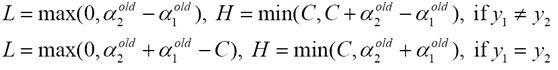
步驟2 計算Ls的二階導數
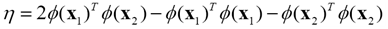
步驟3 更新a2
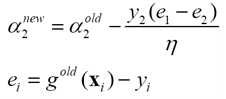
步驟4 計算中間變數
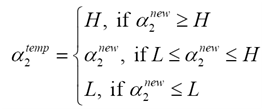
步驟5 更新a1
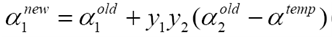
選擇需要更新的乘子需要滿足兩點。
- 任何乘子必須滿足KKT條件
- 對一個滿足KKT條件的乘子進行更新,應能最大限度增大目標函式的值(類似於梯度下降)
SMO演算法的優點,在於
(1)可保證解的全域性最優性,不存在陷入區域性極小解的問題。
(2)分類器複雜度由支撐向量的個數,而非特徵空間的維數決定,因此較少因維數災難發生過擬合現象。
缺點是需要求解二次規劃問題,其規模與訓練量成正比,因此計算複雜度高,且儲存開銷大, 不適用於需進行線上學習的大規模分類問題。
4.LS-SVMSuykens和Vandewalle1999年提出
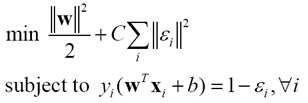 (23)
(23)
與SVM的關鍵不同是約束條件由不等式變為了等式,對應的優化問題
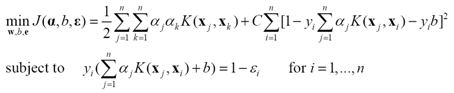 (24)
(24)
不等式變為等式後,拉格朗日乘子可以通過解線性系統得到
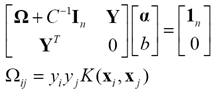 (25)
(25)
解線性系統遠易於解二次規劃問題。但相應地,絕大部分拉格朗日乘子都將不為零。也就是說,LS-SVM分類器的測試時間將長於SVM分類器。
5.SVM最後概述機器學習問題是在已知n個獨立同分布的觀測樣本,在同一組預測函式中求一個最優的函式對依賴關係進行估計,使期望風險R[f]最小。期望風險的大小直觀上可以理解為,當我們用f(x)進行預測時,"平均"的損失程度,或"平均"犯錯誤的程度。損失函式是評價預測準確程度的一種度量,它與預測函式f(x)密切相關。而f(x)的期望風險依賴於概率分佈和損失函式,前者是客觀存在的,後者是根據具體問題選定的,帶有(主觀的)人為的或偏好色彩。
但是,只有樣本卻無法計算期望風險,因此,傳統的學習方法用樣本定義經驗風險Remp[f]作為對期望風險的估計,並設計學習演算法使之最小化。即所謂的經驗風險最小化(Empirical Risk Minimization, ERM)歸納原則。經驗風險是用損失函式來計算的。對於模式識別問題的損失函式來說,經驗風險就是訓練樣本錯誤率;對於函式逼近問題的損失函式來說,就是平方訓練誤差;而對於概率密度估計問題的損失函式來 說,ERM準則就等價於最大似然法。事實上,用ERM準則代替期望風險最小化並沒有經過充分的理論論證,只是直觀上合理的想當然做法。也就是說,經驗風險最小不一定意味著期望風險最小。其實,只有樣本數目趨近於無窮大時,經驗風險才有可能趨近於期望風險。但是很多問題中樣本數目離無窮大很遠,那麼在有限樣本下ERM準則就不一定能使真實風險較小。ERM準則不成功的一個例子就是神經網路的過學習問題(某些情況下,訓練誤差過小反而導致推廣能力下降,或者說是訓練誤差過小導致了預測錯誤率的增加,即真實風險的增加)。
因此,在有限樣本情況下,僅僅用ERM來近似期望風險是行不通的。統計學習理論給出了期望風險R[f]與經驗風險Remp[f]之間關係:R[f] <= ( Remp[f] + e )。其中 e = g(h/n) 為置信區間,e 是VC維 h 的增函式,也是樣本數n的減函式。右端稱為結構風險,它是期望風險 R[f] 的一個上界。經驗風險的最小依賴較大的F(樣本數較多的函式集)中某個 f 的選擇,但是 F 較大,則VC維較大,就導致置信區間 e 變大,所以要想使期望風險 R[f] 最小,必須選擇合適的h和n來使不等式右邊的結構風險最小,這就是結構風險最小化(Structural Risk Minimization, SRM)歸納原則。實現SRM的思路之一就是設計函式集的某種結構使每個子集中都能取得最小的經驗風險(如使訓練誤差為0),然後只需選擇適當的子集使置信範圍最小,則這個子集中使經驗風險最小的函式就是最優函式。SVM方法實際上就是這種思想的具體實現。
SVM是一種基於統計的學習方法,它是對SRM的近似。概括地說,SVM就是首先通過用內積函式定義的非線性變換將輸入空間變換到一個高維空間,然後再在這個空間中求(廣義)最優分類面的分類方法。
