SVM應該是一個應用到數學知識很多的AI演算法，關於KKT的證明花了很長時間，裡面涉及到大量線性代數的知識。

對偶關係、方向導數與梯度的關係、梯度方向與構造的可取區域的關係、拉格朗日乘子引入的真實含義等等。

（一）間隔與支援向量

SVM（support vector machine）支援向量機，最重要的就是在訓練樣本集中找到支援向量。

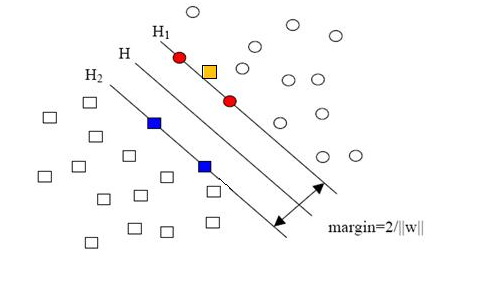
如圖所示為最簡單的二維平面上的分類，要想將圓圈一類和長方形一類分開需要找到一條直線，很顯然這種直線不止一條，但是彷彿又存在一條直線能夠讓兩類點到這條直線的距離取到一個最大值，那麼我們是不是可以通過數學方法來求出這個值和這條分割線呢，答案是可以的。H1和H2這兩條直線上的點就構成了支援向量（只需要這些點就可以求出分類直線），所以在最後的分類中，其餘的點可有可無，當然也就不support啦！

（二）最大化間隔

推廣到n維度，我們需要找到上圖讓margin=2/||w||最大的劃分超平面。

也就是求解帶約束的極值問題，將分割超平面設為為了方便求導，轉換成下面等價問題：

 （三）拉格朗日乘子法與對偶問題

很顯然上述問題是一個凸二次規劃問題，可以先對其使用拉格朗日乘子法得到其對偶問題，對每條約束新增拉格朗日乘子，由於這裡的不是等式約束，所以每條約束

分別對和b求偏導數，得到：

（四）KKT約束條件的詳解

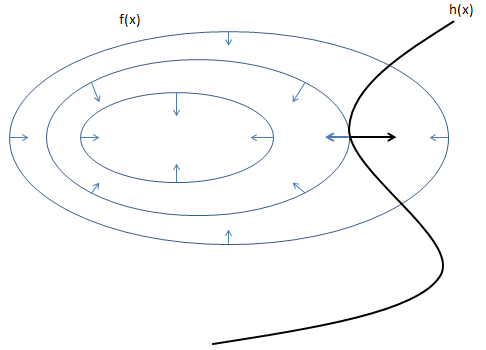
如圖為帶約束的極值情況，數學證明不詳訴，直觀上的集合意義很明確，等高線與約束線相切的時候取得極值。

如圖為不等式約束

陰影部分就是可行域，也就是說可行域從原來的一條線變成了一塊區域。那麼能取到極值點的地方可能有兩種情況：

1. 還是在 h(x)h(x) 和 等值線相切的地方
2. f(x)f(x) 的極值點本身就在可行域裡面。

    可行域是在 g(x)≤0 一側，而 g(x)的梯度指向大於 0 的一側。

       我們求解的目標函式最小值正好與g(x)梯度方向相反

 此時反觀構造的拉格朗日函式，為什麼構造的是：

而不是還有滿足的就很顯然了。

最後整理一下得到三個約束條件：

    這個就是 KKT 條件。它的含義是這個優化問題的極值點一定滿足這組方程組。

（五）拉格朗日乘子的含義

最後補充一點，為什麼拉格朗日乘子可以那麼引入呢？

含義就是在相切的那一點，梯度的方向是一條線上的，由此必然存在：

下一節將介紹SMO演算法，以及在SVM匯入核函式的精彩之處。