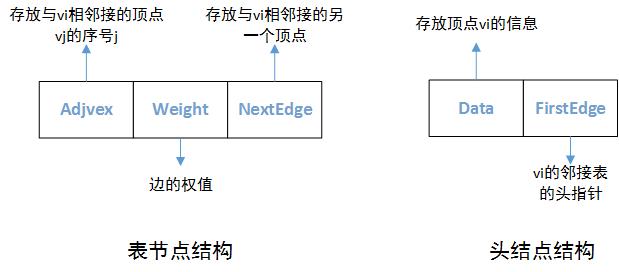
圖的鄰接表表示
阿新 • • 發佈:2019-02-07
描述
圖的表示除了鄰接矩陣表示,還可以使用連結串列陣列。對每個頂點(表頭節點)建立一個單鏈表,第i個單鏈表中節點表示依附於頂點vi 的邊(對有向圖而言,是以頂點vi為尾的弧)。所以在鄰接表中,除了節點外,還有表頭節點。
兩種方法比較
假設圖有V個頂點,E條邊。空間權衡方面,鄰接矩陣使用的空間正比於V^2;而鄰接表所使用的空間正比於V+E。如果邊數較少(也叫稀疏圖),則優先選用鄰接表。若大多數頂點對都由邊相接(也叫稠密圖),則使用鄰接矩陣,避免為不存在的邊分配任何空間。在複雜度方面,鄰接矩陣表示可以在O(n)時間內解決“頂點i和頂點j之間是否存在有邊” 的問題。其他的時候,用鄰接表表示更有效,允許在正比於V+E的時間內而不是V^2的時間內遍歷圖的所有邊
資料結構定義
程式碼實現
#include <iostream>
using namespace std;
#include <stdio.h>
#include <stdlib.h>
#define Max_Vertex_Num 100 //最大頂點數
typedef char VertexType; //頂點數型別定義
typedef int EdgeType; //邊型別定義
typedef struct EdgeNode
{
int adjvex; // 該邊所指的頂點的位置
EdgeType weight; //該邊的權值